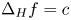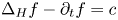1. Introduction and statement of the results
Monotonicity formulas play a prominent role in analysis and geometry. They are often employed in the blowup analysis of a given problem to derive information on the regularity of the solutions, or on their global configurations. In this note we prove two monotonicity formulas, theorems 1.1 and 1.2, in the geometric set-up of Carnot groups. While these Lie groups display some superficial similarities with the Euclidean framework, they are intrinsically non-Riemannian (see Cartan's seminal address [Reference Cartan14]), and the counterpart of many classical results simply fails to be true. Our monotonicity results fall within this category. They are false, in general, if in their statements one replaces the right-invariant carré du champ with the ‘more natural’ left-invariant one.
Our interest in monotonicity formulas stems from our previous joint works [Reference Danielli, Garofalo and Petrosyan19, Reference Danielli, Garofalo and Salsa21] on some nonholonomic free boundary problems suggested to us by people in mechanical engineering and robotics at the Johns Hopkins University. In [Reference Danielli, Garofalo and Salsa21] the optimal interior regularity $\Gamma ^{1,1}_{loc}$![]() of the solution of a certain obstacle problem was established. While such result guarantees the boundedness of the second horizontal derivatives $X_i X_j f$
of the solution of a certain obstacle problem was established. While such result guarantees the boundedness of the second horizontal derivatives $X_i X_j f$![]() of the solution, it falls short of implying their continuity. This critical information was subsequently established in [Reference Danielli, Garofalo and Petrosyan19] in the framework of Carnot groups of step $k=2$
of the solution, it falls short of implying their continuity. This critical information was subsequently established in [Reference Danielli, Garofalo and Petrosyan19] in the framework of Carnot groups of step $k=2$![]() , where it was also proved that, under a suitable thickness assumption, the free boundary is remarkably a $C^{1,\alpha }$
, where it was also proved that, under a suitable thickness assumption, the free boundary is remarkably a $C^{1,\alpha }$![]() non-characteristic hypersurface, suggesting a connection with the sub-Riemannian Bernstein problem, see [Reference Danielli, Garofalo, Nhieu and Pauls18]. The key idea in [Reference Danielli, Garofalo and Petrosyan19] was the systematic use of the right-invariant derivatives in the study of a left-invariant free boundary problemFootnote 1. This leads us to the main theme of this note.
non-characteristic hypersurface, suggesting a connection with the sub-Riemannian Bernstein problem, see [Reference Danielli, Garofalo, Nhieu and Pauls18]. The key idea in [Reference Danielli, Garofalo and Petrosyan19] was the systematic use of the right-invariant derivatives in the study of a left-invariant free boundary problemFootnote 1. This leads us to the main theme of this note.
Given a Carnot group $(\mathbb {G},\,\circ )$![]() , we denote the left-translation operator by ${L_g(g') = g \circ g'}$
, we denote the left-translation operator by ${L_g(g') = g \circ g'}$![]() and with ${\rm d}L_g$
and with ${\rm d}L_g$![]() its differential. The right-translation will be denoted by ${R_g(g') = g' \circ g}$
its differential. The right-translation will be denoted by ${R_g(g') = g' \circ g}$![]() , and its differential by ${\rm d}R_g$
, and its differential by ${\rm d}R_g$![]() . If we fix an orthonormal basis $\{e_1,\,\ldots,\,e_m\}$
. If we fix an orthonormal basis $\{e_1,\,\ldots,\,e_m\}$![]() of the horizontal layer $\mathfrak g_1$
of the horizontal layer $\mathfrak g_1$![]() , then we can define respectively left- and right-invariant vector fields by the formulas
, then we can define respectively left- and right-invariant vector fields by the formulas
More in general, for any $\zeta \in \mathfrak g$![]() we respectively indicate with $Z$
we respectively indicate with $Z$![]() , and $\tilde Z$
, and $\tilde Z$![]() the left- and right-invariant vector fields on $\mathbb {G}$
the left- and right-invariant vector fields on $\mathbb {G}$![]() defined by the Lie formulas
defined by the Lie formulas
For any $\eta,\, \zeta \in \mathfrak g$![]() , for the corresponding vector fields on $\mathbb {G}$
, for the corresponding vector fields on $\mathbb {G}$![]() we have the following simple, yet basic, commutation identities
we have the following simple, yet basic, commutation identities
Such identities can be easily verified using (1.1) and the Baker–Campbell–Hausdorff formula. From (1.2) we have in particular $[X_i,\,\tilde X_j] = 0$![]() , for $i,\, j=1,\,\ldots,\,m$
, for $i,\, j=1,\,\ldots,\,m$![]() . Given a function $f\in C^{1}(\mathbb {G})$
. Given a function $f\in C^{1}(\mathbb {G})$![]() we will respectively denote by
we will respectively denote by

the left- and right-invariant carré du champ of $f$![]() . If we indicate with $e\in \mathbb {G}$
. If we indicate with $e\in \mathbb {G}$![]() the group identity, since $X_i(e) = \tilde X_i(e)$
the group identity, since $X_i(e) = \tilde X_i(e)$![]() for $i=1,\,\ldots,\,m$
for $i=1,\,\ldots,\,m$![]() , we have
, we have
But the two objects in (1.3) are substantially different, except in the trivial situation in which the function $f$![]() depends exclusively on the horizontal variables, see for instance (3.9).
depends exclusively on the horizontal variables, see for instance (3.9).
The left-invariant horizontal Laplacian relative to $\{e_1,\,\ldots,\,e_m\}$![]() is defined on a function $f\in C^{2}(\mathbb {G})$
is defined on a function $f\in C^{2}(\mathbb {G})$![]() by the formula
by the formula

This operator is hypoelliptic thanks to the result in [Reference Hörmander38]. When the step of the stratification of $\mathfrak g$![]() is $k=1$
is $k=1$![]() , then the group is Abelian and $\Delta _H = \Delta$
, then the group is Abelian and $\Delta _H = \Delta$![]() is the standard Laplacian. However, in the genuinely sub-Riemannian situation $k>1$
is the standard Laplacian. However, in the genuinely sub-Riemannian situation $k>1$![]() , the differential operator $\Delta _H$
, the differential operator $\Delta _H$![]() fails to be elliptic at every point of the ambient space $\mathbb {G}$
fails to be elliptic at every point of the ambient space $\mathbb {G}$![]() . We say that a function $f\in C^{2}(\mathbb {G})$
. We say that a function $f\in C^{2}(\mathbb {G})$![]() is subharmonic (superharmonic) if $\Delta _H f \ge 0\ (\le 0)$
is subharmonic (superharmonic) if $\Delta _H f \ge 0\ (\le 0)$![]() . We say that $f$
. We say that $f$![]() is harmonic if it is both sub- and superharmonic. These notions can be extended in the weak variational sense in a standard fashion.
is harmonic if it is both sub- and superharmonic. These notions can be extended in the weak variational sense in a standard fashion.
Let now $\rho$![]() be the pseudo-gauge, centred at $e$
be the pseudo-gauge, centred at $e$![]() , defined in (2.7) of [Reference Greiner34]. Let $B_r = \{g\in \mathbb {G}\mid \rho (g)< r\}$
, defined in (2.7) of [Reference Greiner34]. Let $B_r = \{g\in \mathbb {G}\mid \rho (g)< r\}$![]() and $S_r = \partial B_r$
and $S_r = \partial B_r$![]() . Let $Q>N$
. Let $Q>N$![]() indicate the homogeneous dimension of $\mathbb {G}$
indicate the homogeneous dimension of $\mathbb {G}$![]() associated with the natural anisotropic dilations ($Q = N$
associated with the natural anisotropic dilations ($Q = N$![]() only in the Abelian case $k=1$
only in the Abelian case $k=1$![]() ). Given a function $f\in C(B_1)$
). Given a function $f\in C(B_1)$![]() , and a number $0<\alpha < Q$
, and a number $0<\alpha < Q$![]() , we consider the functional
, we consider the functional
It is easy to verify (see the opening of § 3) that there exists a universal number $\omega _\alpha >0$![]() such that for every $r>0$
such that for every $r>0$![]() one has
one has
As a consequence, one has
We have the following.
Theorem 1.1 (Monotonicity formula)
Let $f$![]() be a solution of $\Delta _H f = c$
be a solution of $\Delta _H f = c$![]() in $B_1,$
in $B_1,$![]() for some $c\in \mathbb {R}$
for some $c\in \mathbb {R}$![]() . Then for any $0<\alpha < Q$
. Then for any $0<\alpha < Q$![]() the functional
the functional
is nondecreasing in $(0,\,1)$![]() . Moreover, we have for every $r\in (0,\,1)$
. Moreover, we have for every $r\in (0,\,1)$![]()
As we have mentioned, theorem 1.1 ceases to be true, and in the worse possible way, if in the definition (1.9) of the functional $\mathscr D_\alpha (f,\,r)$![]() we replace the right-invariant carré du champ $|\tilde {\nabla }_H f|^{2}$
we replace the right-invariant carré du champ $|\tilde {\nabla }_H f|^{2}$![]() with the left-invariant one $|\nabla _H f|^{2}$
with the left-invariant one $|\nabla _H f|^{2}$![]() .
.
Our next result, theorem 1.2, should be seen as a parabolic companion of theorem 1.1. Denote by $p(g,\,g',\,t) = p(g',\,g,\,t)$![]() the smooth, symmetric, strictly positive heat kernel constructed by Folland in [Reference Folland26]. Given a reasonable function $\varphi$
the smooth, symmetric, strictly positive heat kernel constructed by Folland in [Reference Folland26]. Given a reasonable function $\varphi$![]() , the solution of the Cauchy problem $\partial _t f - \Delta _H f = 0$
, the solution of the Cauchy problem $\partial _t f - \Delta _H f = 0$![]() in $\mathbb {G}\times (0,\,\infty )$
in $\mathbb {G}\times (0,\,\infty )$![]() , $f(g,\,0) = \varphi (g)$
, $f(g,\,0) = \varphi (g)$![]() , is given by
, is given by
Theorem 1.2 (Heat monotonicity formula)
Let $f$![]() be a solution of $\partial _t f - \Delta _H f = c$
be a solution of $\partial _t f - \Delta _H f = c$![]() in $\mathbb {G}\times (-1,\,0],$
in $\mathbb {G}\times (-1,\,0],$![]() for some $c\in \mathbb {R},$
for some $c\in \mathbb {R},$![]() and suppose that there exist $A,\, \alpha >0$
and suppose that there exist $A,\, \alpha >0$![]() such that such that for every $g\in \mathbb {G}$
such that such that for every $g\in \mathbb {G}$![]() and $t\in [-1,\,0]$
and $t\in [-1,\,0]$![]() one has
one has
where we have denoted by $d(g,\,g')$![]() the control distance in $\mathbb {G}$
the control distance in $\mathbb {G}$![]() associated with the horizontal layer $\mathfrak g_1$
associated with the horizontal layer $\mathfrak g_1$![]() of the Lie algebra. Then, there exists $T = T(\alpha )>0$
of the Lie algebra. Then, there exists $T = T(\alpha )>0$![]() such that the functional
such that the functional
is nondecreasing in $t\in (0,\,T)$![]() . Furthermore, we have for every $t\in (0,\,T)$
. Furthermore, we have for every $t\in (0,\,T)$![]()
Similarly to theorem 1.1, also theorem 1.2 fails in general if in the definition of $\mathscr I(f,\,t)$![]() we replace $|\tilde {\nabla }_H f|^{2}$
we replace $|\tilde {\nabla }_H f|^{2}$![]() with $|\nabla _H f|^{2}$
with $|\nabla _H f|^{2}$![]() . This failure is caused in both cases by the fact that in sub-Riemannian geometry it is not true in general that if $\Delta _H f = c$
. This failure is caused in both cases by the fact that in sub-Riemannian geometry it is not true in general that if $\Delta _H f = c$![]() , then $|\nabla _H f|^{2}$
, then $|\nabla _H f|^{2}$![]() is subharmonic! There exist harmonic functions $f$
is subharmonic! There exist harmonic functions $f$![]() such that $|\nabla _H f|^{2}$
such that $|\nabla _H f|^{2}$![]() is superharmonic on large regions of $\mathbb {G}$
is superharmonic on large regions of $\mathbb {G}$![]() ! For instance, consider in the Heisenberg group $\mathbb {H}^{1}$
! For instance, consider in the Heisenberg group $\mathbb {H}^{1}$![]() (for this Lie group see the discussion following corollary 3.6) the harmonic functionFootnote 2
(for this Lie group see the discussion following corollary 3.6) the harmonic functionFootnote 2
A calculation shows that
provided that the point $g = (x,\,y,\,\sigma )$![]() belongs to the infinite cylinder $|z|^{2} \le \frac {2}{27}$
belongs to the infinite cylinder $|z|^{2} \le \frac {2}{27}$![]() in $\mathbb {H}^{1}$
in $\mathbb {H}^{1}$![]() . Another example is provided by the harmonic function (1.21). In contrast to (1.15), as a consequence of our right-invariant Bochner identity in proposition 3.4, we show the crucial fact that in any Carnot group $\mathbb {G}$
. Another example is provided by the harmonic function (1.21). In contrast to (1.15), as a consequence of our right-invariant Bochner identity in proposition 3.4, we show the crucial fact that in any Carnot group $\mathbb {G}$![]() a solution of $\Delta _H f = c$
a solution of $\Delta _H f = c$![]() always satisfies globally
always satisfies globally
The reader who is versed in free boundary problems will recognize in theorems 1.1 and 1.2 a resemblance with two deep monotonicity formulas respectively due to Alt–Caffarelli–Friedman (ACF henceforth) for the standard Laplacian [Reference Alt, Caffarelli and Friedman2, lemma 5.1], and to Caffarelli for the classical heat equation [Reference Caffarelli8, theorem 1]. The former states that if one is given in the Euclidean ball $B_1\subset \mathbb {R}^{n}$![]() two continuous functions $f_\pm$
two continuous functions $f_\pm$![]() satisfying
satisfying
then the ACF functional
is nondecreasing for $0< r<1$![]() . This monotonicity formula plays a critical role in free boundary problems with a double phase, see e.g. [Reference Caffarelli and Salsa12] and [Reference Petrosyan, Shahgholian and Uraltseva42], where it is used to show that: (a) $\underset {r\to 0^{+}}{\lim } \Phi (f_+,\,f_-,\,r)$
. This monotonicity formula plays a critical role in free boundary problems with a double phase, see e.g. [Reference Caffarelli and Salsa12] and [Reference Petrosyan, Shahgholian and Uraltseva42], where it is used to show that: (a) $\underset {r\to 0^{+}}{\lim } \Phi (f_+,\,f_-,\,r)$![]() exists, and (b) such limit is less than $\Phi (f_+,\,f_-,\,1)$
exists, and (b) such limit is less than $\Phi (f_+,\,f_-,\,1)$![]() . When $f_{\pm }$
. When $f_{\pm }$![]() are smooth and their supports intersect along a hypersurface $\Sigma$
are smooth and their supports intersect along a hypersurface $\Sigma$![]() through the origin, then the $\underset {r\to 0^{+}}{\lim } \Phi (f_+,\,f_-,\,r)$
through the origin, then the $\underset {r\to 0^{+}}{\lim } \Phi (f_+,\,f_-,\,r)$![]() is the product of the normal derivatives to $\Sigma$
is the product of the normal derivatives to $\Sigma$![]() of $f_{\pm }$
of $f_{\pm }$![]() in $x = 0$
in $x = 0$![]() . Specialized to the case $\mathbb {G} = \mathbb {R}^{n}$
. Specialized to the case $\mathbb {G} = \mathbb {R}^{n}$![]() and $\alpha = 2$
and $\alpha = 2$![]() the functional (1.9) in our theorem 1.1 is precisely half of the ACF functional in (1.16). Similarly, the functional (1.12) in our theorem 1.2 is half of the Caffarelli functional for the heat equation in [Reference Caffarelli8].
the functional (1.9) in our theorem 1.1 is precisely half of the ACF functional in (1.16). Similarly, the functional (1.12) in our theorem 1.2 is half of the Caffarelli functional for the heat equation in [Reference Caffarelli8].
In light of theorems 1.1 and 1.2, and with potential applications to nonholonomic free boundary problems with two phases in mind, it is tempting to propose the following conjecture:
(1) Let $\mathbb {G}$
 be a Carnot group and suppose that in $B_1\subset \mathbb {G}$
be a Carnot group and suppose that in $B_1\subset \mathbb {G}$ we have two continuous functions $f_\pm$
we have two continuous functions $f_\pm$ satisfying
\[f_\pm \ge 0,\quad \Delta_H f_\pm{=}{-} 1,\ f_+{\cdot} f_-{=} 0\ f_+(e) = f_-(e) = 0.\]Prove (or disprove?) that the functional
satisfying
\[f_\pm \ge 0,\quad \Delta_H f_\pm{=}{-} 1,\ f_+{\cdot} f_-{=} 0\ f_+(e) = f_-(e) = 0.\]Prove (or disprove?) that the functional (1.17)\begin{equation} \mathscr D_2(f_+,f_-,r) = \frac{1}{r^{4}} \mathscr D_2(f_+,r) \mathscr D_2(f_-,r) \end{equation}satisfies the following bound for $0< r<1$
(1.17)\begin{equation} \mathscr D_2(f_+,f_-,r) = \frac{1}{r^{4}} \mathscr D_2(f_+,r) \mathscr D_2(f_-,r) \end{equation}satisfies the following bound for $0< r<1$
 (1.18)\begin{equation} \mathscr D_2(f_+,f_-,r) \le C \left\{1 + \mathscr D_2(f_+,1) + \mathscr D_2(f_-,1)\right\}. \end{equation}
(1.18)\begin{equation} \mathscr D_2(f_+,f_-,r) \le C \left\{1 + \mathscr D_2(f_+,1) + \mathscr D_2(f_-,1)\right\}. \end{equation}
(2) Let $\mathbb {G}$
 be a Carnot group and suppose that we have two continuous functions $f_\pm$
be a Carnot group and suppose that we have two continuous functions $f_\pm$ satisfying in $\mathbb {G}\times (-1,\,0]$
satisfying in $\mathbb {G}\times (-1,\,0]$ \[f_\pm \ge 0,\quad (\Delta_H -\partial_t) f_\pm{=}{-} 1,\ f_+{\cdot} f_-{=} 0, \ f_+(e,0) = f_-(e,0) = 0,\]and with moderate growth at infinity. Prove (or disprove?) that the functional
\[f_\pm \ge 0,\quad (\Delta_H -\partial_t) f_\pm{=}{-} 1,\ f_+{\cdot} f_-{=} 0, \ f_+(e,0) = f_-(e,0) = 0,\]and with moderate growth at infinity. Prove (or disprove?) that the functional \[\mathscr I(f_+,f_-,t) = \frac{1}{t^{2}} \mathscr I(f_+,t) \mathscr I(f_-,t)\]satisfies the following bound for $0< t<1$
\[\mathscr I(f_+,f_-,t) = \frac{1}{t^{2}} \mathscr I(f_+,t) \mathscr I(f_-,t)\]satisfies the following bound for $0< t<1$
 (1.19)\begin{equation} \mathscr I(f_+,f_-,t) \le C \left\{1 + \mathscr I(f_+,1) + \mathscr I(f_-,1)\right\}. \end{equation}
(1.19)\begin{equation} \mathscr I(f_+,f_-,t) \le C \left\{1 + \mathscr I(f_+,1) + \mathscr I(f_-,1)\right\}. \end{equation}
Besides the circumstantial evidence provided by theorems 1.1 and 1.2, this conjecture is inspired by the Caffarelli, Jerison and Kenig powerful modification of the ACF monotonicity formula in which the assumption $\Delta f_\pm \ge 0$![]() is replaced by the weaker $\Delta f_\pm \ge -1$
is replaced by the weaker $\Delta f_\pm \ge -1$![]() , and which does not have any ‘monotonicity’ left in its statement, see [Reference Caffarelli, Jerison and Kenig10, theorem1.3]. While when $\mathbb {G} = \mathbb {R}^{n}$
, and which does not have any ‘monotonicity’ left in its statement, see [Reference Caffarelli, Jerison and Kenig10, theorem1.3]. While when $\mathbb {G} = \mathbb {R}^{n}$![]() a uniform bound such as (1.18) appears only remotely connected to the ACF monotonicity (1.16), it does nonetheless lead to the Lipschitz continuity of the solutions, and once this is known than one can go full circle and restore monotonicity, as shown in [Reference Caffarelli, Jerison and Kenig10]. We also cite [Reference Shahgholian43] for various applications of the Caffarelli–Jerison–Kenig result to the $C^{1,1}$
a uniform bound such as (1.18) appears only remotely connected to the ACF monotonicity (1.16), it does nonetheless lead to the Lipschitz continuity of the solutions, and once this is known than one can go full circle and restore monotonicity, as shown in [Reference Caffarelli, Jerison and Kenig10]. We also cite [Reference Shahgholian43] for various applications of the Caffarelli–Jerison–Kenig result to the $C^{1,1}$![]() regularity in free boundary problems, and [Reference Caffarelli and Kenig11, Reference Matevosyan and Petrosyan40] for some remarkable parabolic versions of the monotonicity formula (1.16) and the ‘almost monotonicity’ formulas (1.18) and (1.19).
regularity in free boundary problems, and [Reference Caffarelli and Kenig11, Reference Matevosyan and Petrosyan40] for some remarkable parabolic versions of the monotonicity formula (1.16) and the ‘almost monotonicity’ formulas (1.18) and (1.19).
We reiterate that all the functionals in the above conjectured (1.18) and (1.19) involve the right-invariant carré du champ $|\tilde {\nabla }_H f_\pm |^{2}$![]() . In this respect, we mention that in the recent papers [Reference Ferrari and Forcillo23, Reference Ferrari and Forcillo24] the authors have proposed in the Heisenberg group $\mathbb {H}^{n}$
. In this respect, we mention that in the recent papers [Reference Ferrari and Forcillo23, Reference Ferrari and Forcillo24] the authors have proposed in the Heisenberg group $\mathbb {H}^{n}$![]() a nondecreasing monotonicity formula in which the ACF functional is substituted by the following one containing the left-invariant carré du champ of the functions $f_+$
a nondecreasing monotonicity formula in which the ACF functional is substituted by the following one containing the left-invariant carré du champ of the functions $f_+$![]() and $f_-$
and $f_-$![]()
The same authors have quite recently recognized in [Reference Ferrari and Forcillo25, theorem 1.1] that their conjecture cannot be possibly true. In $\mathbb {H}^{1}$![]() with coordinates $g = (x,\,y,\,\sigma )$
with coordinates $g = (x,\,y,\,\sigma )$![]() they consider the following harmonic function (see the footnote to (1.14))
they consider the following harmonic function (see the footnote to (1.14))
and with rather long calculations they show that
is nonincreasing as $r\in (0,\,r_0)$![]() for a sufficiently small $r_0>0$
for a sufficiently small $r_0>0$![]() . Since on the function (1.21) (but (1.14) would equally work) each half of (1.20) is invariant with respect to the change of variable $(x,\,y,\,\sigma ) \to (-x,\,-y,\,\sigma )$
. Since on the function (1.21) (but (1.14) would equally work) each half of (1.20) is invariant with respect to the change of variable $(x,\,y,\,\sigma ) \to (-x,\,-y,\,\sigma )$![]() (see (3.23)), they infer that
(see (3.23)), they infer that
which shows that

is nonincreasing (instead of nondecreasing) on $(0,\,r_0)$![]() , thus disproving their own conjecture. We emphasize that, instead, neither of the functions (1.14), (1.21) produces a counterexample to our conjecture above. The next result gives a perspective on the negative example (1.21) which is somewhat different from that in [Reference Ferrari and Forcillo25].
, thus disproving their own conjecture. We emphasize that, instead, neither of the functions (1.14), (1.21) produces a counterexample to our conjecture above. The next result gives a perspective on the negative example (1.21) which is somewhat different from that in [Reference Ferrari and Forcillo25].
Proposition 1.3 For the harmonic function (1.21) one has
for every $(x,\,y,\,\sigma )\in \mathbb {H}^{1}$![]() such that $x^{2} + y^{2} \le \frac 19$
such that $x^{2} + y^{2} \le \frac 19$![]() . As a consequence, the left-invariant functional (3.20) is nonincreasing for $r\in (0,\,\frac 13)$
. As a consequence, the left-invariant functional (3.20) is nonincreasing for $r\in (0,\,\frac 13)$![]() for any $0<\alpha < Q$
for any $0<\alpha < Q$![]() . Instead, the right-invariant functional in (1.17) ,
. Instead, the right-invariant functional in (1.17) ,
is nondecreasing on $(0,\,\infty )$![]() .
.
This note contains four sections. Besides the present one, in § 2 we collect some background material that is needed in the rest of the paper. In § 3 we prove theorems 1.1, 1.2 and proposition 1.3, and discuss the role that Bochner formulas plays in these results. In § 4 we discuss another famous monotonicity formula, that of Almgren [Reference Almgren1], and we show that, in accordance with the results in [Reference Garofalo and Lanconelli30, Reference Greiner34], its sub-Riemannian counterpart generically fails. However, the fundamental question of whether or not the frequency (4.1) be locally bounded, remains open at the moment.
In closing, we hope that the present note helps to clarify some of the critical aspects connected to monotonicity in non-Riemannian ambients and at the same time provides an incentive for further understanding.
2. Background material
In this section, we collect some background material that is needed in the rest of the paper. To keep the preliminaries at a minimum and avoid pointless repetitions, we routinely use from now on the definitions and notations from the paper [Reference Greiner34], where some Almgren type monotonicity formulas in Carnot groups and for Baouendi–Grushin operators were obtained (for the latter, see also the first papers on the subject [Reference Garofalo27, Reference Garofalo and Lanconelli30]). A Carnot group of step $k\ge 1$![]() is a simply connected real Lie group $(\mathbb {G},\, \circ )$
is a simply connected real Lie group $(\mathbb {G},\, \circ )$![]() whose Lie algebra $\mathfrak g$
whose Lie algebra $\mathfrak g$![]() is stratified and $k$
is stratified and $k$![]() -nilpotent. This means that there exist vector spaces $\mathfrak g_1,\,\ldots,\,\mathfrak g_k$
-nilpotent. This means that there exist vector spaces $\mathfrak g_1,\,\ldots,\,\mathfrak g_k$![]() such that:
such that:
(i) $\mathfrak g=\mathfrak g_1\oplus \dots \oplus \mathfrak g_k$
 ;
;(ii) $[\mathfrak g_1,\,\mathfrak g_j] = \mathfrak g_{j+1}$
 , $j=1,\,\ldots,\,k-1,\, [\mathfrak g_1,\,\mathfrak g_k] = \{0\}$
, $j=1,\,\ldots,\,k-1,\, [\mathfrak g_1,\,\mathfrak g_k] = \{0\}$ .
.
We assume that $\mathfrak g$![]() is endowed with a scalar product $\langle \cdot,\,\cdot \rangle$
is endowed with a scalar product $\langle \cdot,\,\cdot \rangle$![]() with respect to which the layers $\mathfrak g_j's$
with respect to which the layers $\mathfrak g_j's$![]() , $j=1,\,\ldots,\,r$
, $j=1,\,\ldots,\,r$![]() , are mutually orthogonal. We let $m_j =$
, are mutually orthogonal. We let $m_j =$![]() dim$\, \mathfrak g_j$
dim$\, \mathfrak g_j$![]() , $j= 1,\,\ldots,\,k$
, $j= 1,\,\ldots,\,k$![]() , and denote by $N = m_1 + \cdots + m_k$
, and denote by $N = m_1 + \cdots + m_k$![]() the topological dimension of $\mathbb {G}$
the topological dimension of $\mathbb {G}$![]() . From the assumption (ii) on the Lie algebra it is clear that any basis of the first layer $\mathfrak g_1$
. From the assumption (ii) on the Lie algebra it is clear that any basis of the first layer $\mathfrak g_1$![]() bracket generates the whole of $\mathfrak g$
bracket generates the whole of $\mathfrak g$![]() . Because of such special role $\mathfrak g_1$
. Because of such special role $\mathfrak g_1$![]() is usually called the horizontal layer of the stratification. For ease of notation we henceforth write $m = m_1$
is usually called the horizontal layer of the stratification. For ease of notation we henceforth write $m = m_1$![]() . In the case in which $k =1$
. In the case in which $k =1$![]() one has $\mathfrak g = \mathfrak g_1$
one has $\mathfrak g = \mathfrak g_1$![]() , and thus $\mathbb {G}$
, and thus $\mathbb {G}$![]() is isomorphic to $\mathbb {R}^{m}$
is isomorphic to $\mathbb {R}^{m}$![]() . There is no sub-Riemannian geometry involved and everything is classical. We are primarily interested in the genuinely non-Riemannian setting $k>1$
. There is no sub-Riemannian geometry involved and everything is classical. We are primarily interested in the genuinely non-Riemannian setting $k>1$![]() .
.
Henceforth, given a horizontal Laplacian $\Delta _H$![]() as in (1.5), we indicate with $\Gamma (g,\,g') = \Gamma (g',\,g)$
as in (1.5), we indicate with $\Gamma (g,\,g') = \Gamma (g',\,g)$![]() the unique positive fundamental solution of $-\Delta _H$
the unique positive fundamental solution of $-\Delta _H$![]() which goes to zero at infinity. Such distribution is left-translation invariant, i.e. one has
which goes to zero at infinity. Such distribution is left-translation invariant, i.e. one has
for some function $\tilde \Gamma \in C^{\infty }(\mathbb {G}\setminus \{e\})$![]() , where $e\in \mathbb {G}$
, where $e\in \mathbb {G}$![]() is the group identity. For every $r>0$
is the group identity. For every $r>0$![]() , let
, let
It was proved by Folland in [Reference Folland26] that the distribution $\tilde \Gamma (g)$![]() is homogeneous of degree $2-Q$
is homogeneous of degree $2-Q$![]() with respect to the non-isotropic dilations in $\mathbb {G}$
with respect to the non-isotropic dilations in $\mathbb {G}$![]() associated with the stratification of its Lie algebra $\mathfrak g$
associated with the stratification of its Lie algebra $\mathfrak g$![]() . This implies that, if we define
. This implies that, if we define
then the function $\rho$![]() is homogeneous of degree one. Notice that $\rho \in C^{\infty }(\mathbb {G}\setminus \{e\}) \cap C(\mathbb {G})$
is homogeneous of degree one. Notice that $\rho \in C^{\infty }(\mathbb {G}\setminus \{e\}) \cap C(\mathbb {G})$![]() . We obviously have from (2.1)
. We obviously have from (2.1)
Henceforth, we will use the notation $S_r = \partial B_r$![]() .
.
Next, denote by $p(g,\,g',\,t)$![]() the positive and symmetric heat kernel for $\Delta _H - \partial _t$
the positive and symmetric heat kernel for $\Delta _H - \partial _t$![]() constructed by Folland in [Reference Folland26]. We recall the following result, which combines [Reference Varopoulos, Saloff-Coste and Coulhon44, theorems IV.4.2 and IV.4.3]. In what follows, if $\ell \in \mathbb {N}\cup \{0\}$
constructed by Folland in [Reference Folland26]. We recall the following result, which combines [Reference Varopoulos, Saloff-Coste and Coulhon44, theorems IV.4.2 and IV.4.3]. In what follows, if $\ell \in \mathbb {N}\cup \{0\}$![]() , we consider multi-indices $(j_1,\,\ldots,\,j_\ell )$
, we consider multi-indices $(j_1,\,\ldots,\,j_\ell )$![]() , with $j_1,\,\ldots,\,j_\ell \in \{1,\,\ldots,\,m\}$
, with $j_1,\,\ldots,\,j_\ell \in \{1,\,\ldots,\,m\}$![]() .
.
Theorem 2.1 There exists $C,\, C'>0$![]() such that for all $g,\, g'\in \mathbb {G}$
such that for all $g,\, g'\in \mathbb {G}$![]() and $t>0$
and $t>0$![]() one has
one has
Furthermore, for every $s,\, \ell \in \mathbb {N}\cup \{0\}$![]() and $\varepsilon >0,$
and $\varepsilon >0,$![]() there exists $C>0$
there exists $C>0$![]() such that for all $g,\, g'\in \mathbb {G}$
such that for all $g,\, g'\in \mathbb {G}$![]() and $t>0$
and $t>0$![]() one has
one has
The heat semigroup $P_t = {\rm e}^{-t \Delta _H}$![]() is defined on a reasonable function $f:\mathbb {G}\to \mathbb {R}$
is defined on a reasonable function $f:\mathbb {G}\to \mathbb {R}$![]() by the formula
by the formula
Similarly to the classical case, the function $u(g,\,t) = P_t f(g)$![]() is smooth in $\mathbb {G}\times (0,\,\infty )$
is smooth in $\mathbb {G}\times (0,\,\infty )$![]() and solves the Cauchy problem
and solves the Cauchy problem
If we assume that there exist $A,\, \alpha >0$![]() such that for every $g\in \mathbb {G}$
such that for every $g\in \mathbb {G}$![]() one has
one has
where we have denoted by $d(g,\,g')$![]() the control distance in $\mathbb {G}$
the control distance in $\mathbb {G}$![]() associated with the horizontal layer $\mathfrak g_1$
associated with the horizontal layer $\mathfrak g_1$![]() of the Lie algebra, then the semigroup $P_t f(g)$
of the Lie algebra, then the semigroup $P_t f(g)$![]() is well-defined, at least for $0< t< T$
is well-defined, at least for $0< t< T$![]() , where $T = T(\alpha )>0$
, where $T = T(\alpha )>0$![]() is sufficiently small. For this it suffices to observe that, if $T < {1}/({4(1+\varepsilon )\alpha })$
is sufficiently small. For this it suffices to observe that, if $T < {1}/({4(1+\varepsilon )\alpha })$![]() , then for $0< t< T$
, then for $0< t< T$![]() one has for any $g\in \mathbb {G}$
one has for any $g\in \mathbb {G}$![]()
For $r>0$![]() consider now the parabolic cylinders
consider now the parabolic cylinders
As a special case of [Reference Danielli and Garofalo17, theorem 1.1] we obtain the following.
Theorem 2.2 Suppose that $f$![]() solves $\Delta _H f - \partial _t f= c$
solves $\Delta _H f - \partial _t f= c$![]() in $\mathbb {G}\times \mathbb {R},$
in $\mathbb {G}\times \mathbb {R},$![]() for some $c\in \mathbb {R}$
for some $c\in \mathbb {R}$![]() . For every $s,\, \ell \in \mathbb {N} \cup \{0\}$
. For every $s,\, \ell \in \mathbb {N} \cup \{0\}$![]() and $r>0,$
and $r>0,$![]() one has
one has
for some constant $C=C(c,\,s,\,\ell )>0$![]() .
.
3. Proof of theorems 1.1, 1.2 and proposition 1.3
In this section, we prove theorems 1.1 and 1.2, as well as proposition 1.3. With these preliminaries in place, we now return to the functional (1.6) and observe that, since the function $g\to \rho (g)$![]() is homogeneous of degree one with respect to the nonisotropic group dilations $\{\delta _\lambda \}_{\lambda >0}$
is homogeneous of degree one with respect to the nonisotropic group dilations $\{\delta _\lambda \}_{\lambda >0}$![]() , while $g\to |\nabla _H\rho (g)|^{2}$
, while $g\to |\nabla _H\rho (g)|^{2}$![]() is homogeneous of degree zero with respect to the same, the change of variable $g' = \delta _r(g)$
is homogeneous of degree zero with respect to the same, the change of variable $g' = \delta _r(g)$![]() , for which ${\rm d}g' = r^{Q} {\rm d}g$
, for which ${\rm d}g' = r^{Q} {\rm d}g$![]() , immediately gives
, immediately gives
This proves (1.7). The statement (1.8) immediately follows from the continuity of $f$![]() and from (1.7).
and from (1.7).
Next, we record the following equation (see [Reference Greiner34, formula (3.12)] or also the earlier work [Reference Citti, Garofalo and Lanconelli15] for a more general result), valid for any function $\psi \in C^{2}(\mathbb {G})$![]() ,
,
Equation (3.1) represents a generalization of Gaveau's mean value formula in [Reference Gaveau35] for harmonic functions in the Heisenberg group $\mathbb {H}^{n}$![]() . Differentiating with respect to $r$
. Differentiating with respect to $r$![]() in (3.1) we obtain
in (3.1) we obtain
From (3.2) we immediately infer the following result.
Lemma 3.1 Suppose that $\psi \in C^{2}(B_1)$![]() . If $\Delta _H \psi \ge 0$
. If $\Delta _H \psi \ge 0$![]() ($\le 0$
($\le 0$![]() ) in $B_1$
) in $B_1$![]() then the averages
then the averages
are nondecreasing (nonincreasing) in $r\in (0,\,1)$![]() .
.
Returning to the functional $\mathscr D_\alpha (f,\,r)$![]() , we have the following simple, yet important, fact.
, we have the following simple, yet important, fact.
Proposition 3.2 Suppose that the surface averages of $f$![]() ,
,
are nondecreasing (nonincreasing) in $r\in (0,\,1)$![]() . Then $r\to \mathscr D_\alpha (f,\,r)$
. Then $r\to \mathscr D_\alpha (f,\,r)$![]() is nondecreasing (nonincreasing) in $(0,\,1)$
is nondecreasing (nonincreasing) in $(0,\,1)$![]() and we have for every $r\in (0,\,1)$
and we have for every $r\in (0,\,1)$![]()
where $\omega _\alpha >0$![]() is the universal constant in (1.7).
is the universal constant in (1.7).
Proof. Using Federer's coarea formula to differentiate (1.6) one has
Assume that (3.3) are nondecreasing in $r\in (0,\,1)$![]() . Again the coarea formula gives
. Again the coarea formula gives

This proves that $\mathscr D_\alpha '(r)\ge 0$![]() for $r\in (0,\,1)$
for $r\in (0,\,1)$![]() . Similarly, one proves that $\mathscr D_\alpha '(r)\le 0$
. Similarly, one proves that $\mathscr D_\alpha '(r)\le 0$![]() if (3.3) are nonincreasing. The second part of proposition 3.2 is a direct consequence of the first, and of (1.8).
if (3.3) are nonincreasing. The second part of proposition 3.2 is a direct consequence of the first, and of (1.8).
Remark 3.3 Since in view of lemma 3.1 the monotonicity of (3.3) characterizes sub- and superharmonicity, a similar monotonicity holds true for $r\to \mathscr D_\alpha (f,\,r)$![]() if $f$
if $f$![]() is sub- or superharmonic in $B_1$
is sub- or superharmonic in $B_1$![]() .
.
We next recall that the celebrated identity of Bochner states that on a Riemannian manifold $M$![]() one has for $f\in C^{3}(M)$
one has for $f\in C^{3}(M)$![]()
where $\operatorname {Ric}(\cdot,\,\cdot )$![]() indicates the Ricci tensor on $M$
indicates the Ricci tensor on $M$![]() , see e.g. [Reference Chow, Lu and Ni16, § 4.3 on p. 18]. This implies in particular that if $\Delta f = c$
, see e.g. [Reference Chow, Lu and Ni16, § 4.3 on p. 18]. This implies in particular that if $\Delta f = c$![]() for some $c\in \mathbb {R}$
for some $c\in \mathbb {R}$![]() , and $\operatorname {Ric}(\cdot,\,\cdot )\ge 0$
, and $\operatorname {Ric}(\cdot,\,\cdot )\ge 0$![]() , then
, then
As we will see next, in sub-Riemannian geometry the fundamental subharmonicity property (3.6) fails miserably. This negative situation can be remedied by bringing the right-invariant vector fields $\tilde X_i$![]() to centre stage. As we have mentioned, in free boundary problems the idea of working with right-invariant derivatives was first systematically developed in [Reference Danielli, Garofalo and Petrosyan19] to establish the $C^{1,\alpha }$
to centre stage. As we have mentioned, in free boundary problems the idea of working with right-invariant derivatives was first systematically developed in [Reference Danielli, Garofalo and Petrosyan19] to establish the $C^{1,\alpha }$![]() regularity of the free boundary in the non-holonomic obstacle problem. A related perspective was further exploited in [Reference Garofalo29] to prove $C^{1,\alpha }$
regularity of the free boundary in the non-holonomic obstacle problem. A related perspective was further exploited in [Reference Garofalo29] to prove $C^{1,\alpha }$![]() regularity via maximum principles, and subsequently in the study of fully nonlinear equations in [Reference Martino and Montanari39], and of sub-Riemannian mean curvature flow in [Reference Capogna, Citti and Manfredini13].
regularity via maximum principles, and subsequently in the study of fully nonlinear equations in [Reference Martino and Montanari39], and of sub-Riemannian mean curvature flow in [Reference Capogna, Citti and Manfredini13].
Proposition 3.4 (Right Bochner type identity)
Let $\mathbb {G}$![]() be a Carnot group, $f\in C^{3}(\mathbb {G}),$
be a Carnot group, $f\in C^{3}(\mathbb {G}),$![]() then one has
then one has

If in particular $\Delta _H f = c,$![]() for some $c\in \mathbb {R},$
for some $c\in \mathbb {R},$![]() then we have
then we have

Proof. The proof is a straightforward calculation that uses the commutation identities $[X_i,\,\tilde X_j] = 0$![]() , $i,\, j =1,\,\ldots,\,m$
, $i,\, j =1,\,\ldots,\,m$![]() . We leave the details to the interested reader.
. We leave the details to the interested reader.
We emphasize that the two objects $|\tilde {\nabla }_H f|^{2}$![]() and $|\nabla _H f|^{2}$
and $|\nabla _H f|^{2}$![]() differ substantially. For instance, in the special case in which $\mathbb {G}$
differ substantially. For instance, in the special case in which $\mathbb {G}$![]() is a group of step $k=2$
is a group of step $k=2$![]() , with group constants $b^{\ell }_{ij}$
, with group constants $b^{\ell }_{ij}$![]() , and (logarithmic) coordinates $g = (z_1,\,\ldots,\,z_m,\,\sigma _1,\,\ldots,\,\sigma _{m_2})$
, and (logarithmic) coordinates $g = (z_1,\,\ldots,\,z_m,\,\sigma _1,\,\ldots,\,\sigma _{m_2})$![]() , one has
, one has

see [Reference Garofalo29, lemma 2.3].
We can now present the
Proof of theorem 1.1. Suppose $\Delta _H f = c$![]() in $B_1$
in $B_1$![]() . By hypoellipticity, we know that $f\in C^{\infty }(B_1)$
. By hypoellipticity, we know that $f\in C^{\infty }(B_1)$![]() . At this point the desired conclusion is an immediate consequence of proposition 3.4, lemma 3.1 and proposition 3.2.
. At this point the desired conclusion is an immediate consequence of proposition 3.4, lemma 3.1 and proposition 3.2.
Next we present the
Proof of theorem 1.2. Let $f$![]() be a solution of $\partial _t f - \Delta _H f = c$
be a solution of $\partial _t f - \Delta _H f = c$![]() in the infinite slab $\mathbb {G}\times (-1,\,0)$
in the infinite slab $\mathbb {G}\times (-1,\,0)$![]() . By the hypoellipticity result in [Reference Hörmander38], we know that $f\in C^{\infty }(\mathbb {G}\times (-1,\,0))$
. By the hypoellipticity result in [Reference Hörmander38], we know that $f\in C^{\infty }(\mathbb {G}\times (-1,\,0))$![]() . However, now we cannot proceed as in the proof of theorem 1.1 since the set of integration is not a relatively compact set (the pseudoballs $B_r$
. However, now we cannot proceed as in the proof of theorem 1.1 since the set of integration is not a relatively compact set (the pseudoballs $B_r$![]() ). To make sense of the integral in (1.12) on a sufficiently small interval $t\in (0,\,T)$
). To make sense of the integral in (1.12) on a sufficiently small interval $t\in (0,\,T)$![]() and be able to differentiate it with respect to the parameter $t\in (-1,\,0)$
and be able to differentiate it with respect to the parameter $t\in (-1,\,0)$![]() , we use the assumption (1.11). Note that we can write (1.12) as follows
, we use the assumption (1.11). Note that we can write (1.12) as follows
provided that the function $u(g,\,t) = |\tilde {\nabla }_H f(g,\,-t)|^{2})$![]() is such that the integral defining
is such that the integral defining
be finite. From theorem 2.2 we now have for every $\ell \in \mathbb {N}$![]() and $r>0$
and $r>0$![]()
where in the last inequality we have used (1.11) and the fact that $|Q_{2r}| = 4r^{2} |B_{2r}|$![]() . From (3.11) it is easy to show that $X_{j_1}X_{j_2}\ldots X_{j_\ell } f$
. From (3.11) it is easy to show that $X_{j_1}X_{j_2}\ldots X_{j_\ell } f$![]() satisfies the same uniform estimate in (1.11) as $f$
satisfies the same uniform estimate in (1.11) as $f$![]() . Since any right-invariant derivative $\tilde X_j f$
. Since any right-invariant derivative $\tilde X_j f$![]() can be expressed in terms of the vector fields $X_j$
can be expressed in terms of the vector fields $X_j$![]() and a certain number of combinations, with polynomial coefficients, of terms $X_{j_1}X_{j_2}\ldots X_{j_\ell } f$
and a certain number of combinations, with polynomial coefficients, of terms $X_{j_1}X_{j_2}\ldots X_{j_\ell } f$![]() , by (3.11) we obtain a similar a priori estimate for $|\tilde {\nabla }_H f|^{2}$
, by (3.11) we obtain a similar a priori estimate for $|\tilde {\nabla }_H f|^{2}$![]() , possibly with a larger coefficient $\alpha >0$
, possibly with a larger coefficient $\alpha >0$![]() in the exponential. This implies that $P_\tau (|\tilde {\nabla }_H f(\cdot,\,-\tau )|^{2})(e)$
in the exponential. This implies that $P_\tau (|\tilde {\nabla }_H f(\cdot,\,-\tau )|^{2})(e)$![]() is well-defined for $0<\tau < T$
is well-defined for $0<\tau < T$![]() , for some $T= T(\alpha )>0$
, for some $T= T(\alpha )>0$![]() (see the discussion prior to theorem 2.2). Differentiating (3.10) we thus find for every $t\in (0,\,T)$
(see the discussion prior to theorem 2.2). Differentiating (3.10) we thus find for every $t\in (0,\,T)$![]()
We infer that $t \longrightarrow \mathscr I(|\tilde {\nabla }_H f|^{2},\,t)$![]() is nondecreasing (nonincreasing) in $(0,\,T)$
is nondecreasing (nonincreasing) in $(0,\,T)$![]() if and only if we have for every $t\in (0,\,T)$
if and only if we have for every $t\in (0,\,T)$![]()
We next differentiate the functional in the right-hand side of (3.12) obtaining by the chain rule

where in the last equality in (3.13) we have used (3.7) in proposition 3.4. Since we are assuming that $\Delta _H f-\partial _t f = c$![]() in $\mathbb {G}\times (-1,\,0)$
in $\mathbb {G}\times (-1,\,0)$![]() , we infer from (3.13)
, we infer from (3.13)

therefore the functional $t \longrightarrow P_t(|\tilde {\nabla }_H f(\cdot,\,-t)|^{2})(e)$![]() is nondecreasing. This implies
is nondecreasing. This implies
which finally proves (3.12), and therefore the nondecreasing monotonicity of $t\longrightarrow \mathscr I(|\tilde {\nabla }_H f|^{2},\,t)$![]() .
.
Having established the positive results, we next discuss the typically non-Riemannian phenomenon for which theorems 1.1 and 1.2 fail if in their statement one replaces the right-invariant carré du champ with the left-invariant one $|\nabla _H f|^{2}$![]() . We recall the following result which is [Reference Garofalo28, proposition 3.3].
. We recall the following result which is [Reference Garofalo28, proposition 3.3].
Proposition 3.5 (Left Bochner type identity)
Let $\mathbb {G}$![]() be a Carnot group, $f\in C^{3}(\mathbb {G}),$
be a Carnot group, $f\in C^{3}(\mathbb {G}),$![]() then one has
then one has

In (3.16) we have denoted by $\nabla _H^{2} f = [f_{ij}]$![]() the symmetrized horizontal Hessian of $f$
the symmetrized horizontal Hessian of $f$![]() with entries
with entries
When $\mathbb {G}$![]() is of step $2$
is of step $2$![]() , then $[X_i,\,[X_i,\,X_j]] = 0$
, then $[X_i,\,[X_i,\,X_j]] = 0$![]() and we obtain from proposition 3.5.
and we obtain from proposition 3.5.
Corollary 3.6 Let $\mathbb {G}$![]() be a Carnot group of step $k=2,$
be a Carnot group of step $k=2,$![]() $f\in C^{3}(\mathbb {G}),$
$f\in C^{3}(\mathbb {G}),$![]() then one has
then one has

The problem with (3.16) is that, even if $\Delta _H f = 0$![]() , the term $4 \sum _{i,j=1}^{m} X_j f [X_i,\,X_j] X_i f$
, the term $4 \sum _{i,j=1}^{m} X_j f [X_i,\,X_j] X_i f$![]() can prevail so badly on the positive terms, to reverse the sign of the sum in the right-hand side. We have already hinted to this phenomenon with the example (1.14), see (1.15). For the reader's understanding, we next discuss this aspect in more detail. Consider the Heisenberg group $\mathbb {G} = \mathbb {H}^{n}$
can prevail so badly on the positive terms, to reverse the sign of the sum in the right-hand side. We have already hinted to this phenomenon with the example (1.14), see (1.15). For the reader's understanding, we next discuss this aspect in more detail. Consider the Heisenberg group $\mathbb {G} = \mathbb {H}^{n}$![]() with the left-invariant basis of the Lie algebra given by
with the left-invariant basis of the Lie algebra given by
If we let $T = \partial _\sigma$![]() , then the only nontrivial commutators are $[X_i,\,X_{n+j}] = T \delta _{ij}$
, then the only nontrivial commutators are $[X_i,\,X_{n+j}] = T \delta _{ij}$![]() , and we find
, and we find

Similarly, we have

where we have denoted by $\nabla _H^{\perp } u = (X_{n+1}u,\,\ldots,\,X_{2n}u,\, - X_1 u,\,\ldots,\,-X_n u)$![]() . Substituting the latter two equations in (3.16) we obtain
. Substituting the latter two equations in (3.16) we obtain

Now, if $\Delta _H f = c$![]() , with $c\in \mathbb {R}$
, with $c\in \mathbb {R}$![]() , then one has from (3.18)
, then one has from (3.18)
The following discussion shows that the term $4 \langle \nabla _H(Tf),\,\nabla _H^{\perp } f\rangle$![]() can destroy the subharmonicity of $|\nabla _H f|^{2}$
can destroy the subharmonicity of $|\nabla _H f|^{2}$![]() . Consider the harmonic function (1.21) from the work [Reference Ferrari and Forcillo25, § 5], but (1.14) would work equally well. Such function is the sum of two solid harmonics of degree one and three. Greiner first computed such solid harmonics in $\mathbb {H}^{1}$
. Consider the harmonic function (1.21) from the work [Reference Ferrari and Forcillo25, § 5], but (1.14) would work equally well. Such function is the sum of two solid harmonics of degree one and three. Greiner first computed such solid harmonics in $\mathbb {H}^{1}$![]() , see [Reference Greiner36, p. 387], and Dunkl subsequently generalized his results to $\mathbb {H}^{n}$
, see [Reference Greiner36, p. 387], and Dunkl subsequently generalized his results to $\mathbb {H}^{n}$![]() in [Reference Dunkl22]. The subject has since somewhat languished for lack of a complete understanding of some fundamental orthogonality and completeness issues, see the unpublished preprint [Reference Greiner and Koornwinder37, p. 29], but also the discussion in § 4.
in [Reference Dunkl22]. The subject has since somewhat languished for lack of a complete understanding of some fundamental orthogonality and completeness issues, see the unpublished preprint [Reference Greiner and Koornwinder37, p. 29], but also the discussion in § 4.
Proof of proposition 1.3. Instead of the lengthy calculations based on spherical harmonics in [Reference Ferrari and Forcillo25, § 4, 5], we disprove the nondecreasing monotonicity of the left-invariant functional
by simply observing that, on the function (1.21), we have $\Delta _H(|\nabla _H f|^{2})\le 0$![]() in an infinite cylinder in $\mathbb {H}^{1}$
in an infinite cylinder in $\mathbb {H}^{1}$![]() . We then use lemma 3.1 and proposition 3.2 to deduce the nonincreasing monotonicity of (3.20). From (1.21) and (3.17) simple computations give
. We then use lemma 3.1 and proposition 3.2 to deduce the nonincreasing monotonicity of (3.20). From (1.21) and (3.17) simple computations give
and furthermore
In particular $\Delta _H f = 0$![]() in $\mathbb {H}^{1}$
in $\mathbb {H}^{1}$![]() (this conclusion is also obvious from the fact that $f$
(this conclusion is also obvious from the fact that $f$![]() is the sum of two harmonic polynomials). Using (3.21) we now find
is the sum of two harmonic polynomials). Using (3.21) we now find
We next prove that, contrarily to the Riemannian case (3.5), the function $|\nabla _H f|^{2}$![]() badly fails to be subharmonic. We compute from (3.23)
badly fails to be subharmonic. We compute from (3.23)

and

Next,
and

Combining the latter two equations we find
It is now clear from (3.24) that
provided that $|z|^{2} \le \frac 19$![]() . From lemma 3.1 and proposition 3.2 we conclude that for the harmonic function $f$
. From lemma 3.1 and proposition 3.2 we conclude that for the harmonic function $f$![]() in (1.21) the functional
in (1.21) the functional
is nonincreasing for $r\in (0,\,1/3)$![]() !
!
For the second part of the proposition we need to compute $|\tilde {\nabla }_H f|^{2}$![]() . We have
. We have
and therefore
By (3.26), the fact that $|\nabla _H \rho |^{2} = {|z|^{2}}/{\rho ^{2}}$![]() , and the change of variable $(x,\,y,\,\sigma )\to (-x,\,-y,\,\sigma )$
, and the change of variable $(x,\,y,\,\sigma )\to (-x,\,-y,\,\sigma )$![]() (see [Reference Ferrari and Forcillo25, formula (6.2)]), we easily recognize that
(see [Reference Ferrari and Forcillo25, formula (6.2)]), we easily recognize that
Therefore, thanks to (3.8) in proposition 3.4 and our theorem 1.1, we know that
As a consequence, we infer that $r \longrightarrow \mathscr D_2(f_+,\,f_-,\,r) = \frac 14 \mathscr D_2(f,\,r)^{2}$![]() is nondecreasing on $(0,\,\infty )$
is nondecreasing on $(0,\,\infty )$![]() .
.
Remark 3.7 It is interesting to observe that with $f$![]() as in (1.21) we have instead in the entire space $\mathbb {H}^{1}$
as in (1.21) we have instead in the entire space $\mathbb {H}^{1}$![]()
As a consequence, the functional $r\ \longrightarrow \ \mathscr D_2(|\nabla _H f|^{2}+ \frac 13 (Tf)^{2},\,r)$![]() is globally nondecreasing.
is globally nondecreasing.
4. Failure of Almgren monotonicity formula in sub-Riemannian geometry
In this final section, we discuss the sub-Riemannian counterpart of another celebrated monotonicity formula from geometric PDEs. We recall that, in its simplest form, Almgren monotonicity formula states that if $\Delta f = 0$![]() in $B_1\subset \mathbb {R}^{n}$
in $B_1\subset \mathbb {R}^{n}$![]() , then its frequency
, then its frequency

is nondecreasing, see [Reference Almgren1]. This result plays a fundamental role in several areas of analysis and geometry, ranging from minimal surfaces, to unique continuation for elliptic and parabolic PDEs, and more recently free boundaries in which the obstacle is confined to a lower-dimensional manifold. We refer in particular to the papers [Reference Garofalo and Lin31, Reference Garofalo and Lin32], and to the more recent works [Reference Athanasopoulos, Caffarelli and Salsa3, Reference Banerjee, Danielli, Garofalo and Petrosyan5, Reference Banerjee and Garofalo6, Reference Caffarelli, Salsa and Silvestre9, Reference Danielli, Garofalo, Petrosyan and To20, Reference Garofalo and Petrosyan33].
In sub-Riemannian geometry the horizontal Laplacian (1.5) is not real-analytic hypoelliptic in general, and a fundamental open question is whether harmonic functions have the unique continuation property (ucp). An initial very interesting study of what can go wrong for smooth, even compactly supported, perturbations of (1.5) was done by Bahouri in [Reference Bahouri4]. However, Bahouri's work does not provide any evidence, in favour or to the contrary, about the ucp for harmonic functions in a Carnot group. The reader is referred to [Reference Greiner34] for a detailed discussion. In the same paper, the authors have shown that, in a Carnot group $\mathbb {G}$![]() , given a harmonic function $f$
, given a harmonic function $f$![]() in a ball $B_1 \subset \mathbb {G}$
in a ball $B_1 \subset \mathbb {G}$![]() , the following sub-Riemannian analogue of Almgren frequency
, the following sub-Riemannian analogue of Almgren frequency

is nondecreasing in $r\in (0,\,1)$![]() provided that $f$
provided that $f$![]() has vanishing discrepancy, see also [Reference Garofalo and Lanconelli30] for the first result in this direction in $\mathbb {H}^{n}$
has vanishing discrepancy, see also [Reference Garofalo and Lanconelli30] for the first result in this direction in $\mathbb {H}^{n}$![]() . In the surface integral in (4.1) the symbol ${\rm d}\sigma _H$
. In the surface integral in (4.1) the symbol ${\rm d}\sigma _H$![]() denotes the horizontal perimeter measure. It is obvious that if the frequency is nondecreasing on an interval $(0,\,r_0)$
denotes the horizontal perimeter measure. It is obvious that if the frequency is nondecreasing on an interval $(0,\,r_0)$![]() , then one has in particular $N(f,\,\cdot )\in L^{\infty }(0,\,r_0)$
, then one has in particular $N(f,\,\cdot )\in L^{\infty }(0,\,r_0)$![]() . In [Reference Greiner34, theorem 4.3] it was shown that, in fact, the local boundedness of $N(f,\,\cdot )$
. In [Reference Greiner34, theorem 4.3] it was shown that, in fact, the local boundedness of $N(f,\,\cdot )$![]() is necessary and sufficient for the following doubling condition
is necessary and sufficient for the following doubling condition
It is well-known by now (see [Reference Garofalo and Lin31]) that (4.2) implies the strong unique continuation property for $f$![]() .
.
In a Carnot group $\mathbb {G}$![]() the local boundedness of the frequency of a harmonic function $f$
the local boundedness of the frequency of a harmonic function $f$![]() is a fundamental open problem (to be proved, or disproved). In [Reference Greiner34, theorem 8.1] it was shown that (4.2) is true for harmonic functions in a Metivier group, and therefore in such Lie groups (which include those of Heisenberg type) the frequency (4.1) is locally bounded. The following discussion shows that not even in $\mathbb {H}^{n}$
is a fundamental open problem (to be proved, or disproved). In [Reference Greiner34, theorem 8.1] it was shown that (4.2) is true for harmonic functions in a Metivier group, and therefore in such Lie groups (which include those of Heisenberg type) the frequency (4.1) is locally bounded. The following discussion shows that not even in $\mathbb {H}^{n}$![]() one should expect the frequency to be generically nondecreasing. We emphasize that this phenomenon of monotonicity versus boundedness is connected to the ‘almost monotonicity’ character of the conjecture in § 3.
one should expect the frequency to be generically nondecreasing. We emphasize that this phenomenon of monotonicity versus boundedness is connected to the ‘almost monotonicity’ character of the conjecture in § 3.
We recall that in [Reference Greiner34, proposition. 3.6] it was shown that if $f$![]() is harmonic in a Carnot group, then
is harmonic in a Carnot group, then
where $Z$![]() denotes the generator of the group dilations in $\mathbb {G}$
denotes the generator of the group dilations in $\mathbb {G}$![]() . Combining (4.1) with (4.3) we see that we can express the frequency in the useful alternative fashion
. Combining (4.1) with (4.3) we see that we can express the frequency in the useful alternative fashion

We emphasize that (4.4) does immediately imply that if $f$![]() is a harmonic function homogeneous of degree $\kappa$
is a harmonic function homogeneous of degree $\kappa$![]() , then $N(f,\,r) \equiv \kappa$
, then $N(f,\,r) \equiv \kappa$![]() . We do not know whether the opposite implication holds in general! The main reason is that, even when $\mathbb {G} = \mathbb {R}^{n}$
. We do not know whether the opposite implication holds in general! The main reason is that, even when $\mathbb {G} = \mathbb {R}^{n}$![]() , the only known proof of such implication seem to crucially rest on the full-strength of Almgren monotonicity formula.
, the only known proof of such implication seem to crucially rest on the full-strength of Almgren monotonicity formula.
Suppose now that $P_h$![]() and $P_k$
and $P_k$![]() are two harmonic functions in $\mathbb {G}$
are two harmonic functions in $\mathbb {G}$![]() , respectively of homogeneous degree $h\not = 0$
, respectively of homogeneous degree $h\not = 0$![]() and $k\not = 0$
and $k\not = 0$![]() , and suppose to fix the ideas that $h< k$
, and suppose to fix the ideas that $h< k$![]() . If $f = P_h + P_k$
. If $f = P_h + P_k$![]() , we have
, we have
Inserting this information in (4.4) we find

It is clear from (4.5) that on a harmonic function of the type $f = P_h + P_k$![]() the frequency is nondecreasing if and only if such is the quantity
the frequency is nondecreasing if and only if such is the quantity

Suppose that, similarly to the case $\mathbb {G} = \mathbb {R}^{n}$![]() , we knew
, we knew

From (4.6) we would immediately infer by rescaling (${\rm d}\sigma _H \circ \delta _r = r^{Q-1} {\rm d}\sigma _H$![]() ) that
) that
and this would easily imply $\mathscr E'(r) \ge 0$![]() . But in sub-Riemannian geometry the ‘Euclidean’ looking identity (4.6) fails to be true in general. This negative phenomenon was already brought to light in the context of $\mathbb {H}^{n}$
. But in sub-Riemannian geometry the ‘Euclidean’ looking identity (4.6) fails to be true in general. This negative phenomenon was already brought to light in the context of $\mathbb {H}^{n}$![]() in [Reference Garofalo and Lanconelli30, theorem 1.1], and this is why that result contained the additional assumption (1.19), and in [Reference Greiner34, definition 5.1] the notion of discrepancy was introduced. What is true, instead, in any Carnot group, is the following formula
in [Reference Garofalo and Lanconelli30, theorem 1.1], and this is why that result contained the additional assumption (1.19), and in [Reference Greiner34, definition 5.1] the notion of discrepancy was introduced. What is true, instead, in any Carnot group, is the following formula
but, as we next show, (4.7) is a far cry from its Euclidean counterpart containing the Euler vector field and the Euclidean norm. To understand this comment we recall [Reference Greiner34, lemma 6.8] (see also [Reference Garofalo and Lanconelli30, formula (2.22)] for $\mathbb {H}^{n}$![]() ), that states that when $\mathbb {G}$
), that states that when $\mathbb {G}$![]() is a group of Heisenberg type, with logarithmic coordinates $g = (z,\,\sigma )$
is a group of Heisenberg type, with logarithmic coordinates $g = (z,\,\sigma )$![]() , then for $f\in C^{1}(\mathbb {G})$
, then for $f\in C^{1}(\mathbb {G})$![]() one has
one has

where
The vector fields $\Theta _\ell$![]() , which come from the complex structure of $\mathbb {G}$
, which come from the complex structure of $\mathbb {G}$![]() , are the reason for the failure of (4.6), and in view of (3.9) also of the failure of the nondecreasing character of theorems 1.1 and 1.2 if we change $|\tilde {\nabla }_H f|^{2}$
, are the reason for the failure of (4.6), and in view of (3.9) also of the failure of the nondecreasing character of theorems 1.1 and 1.2 if we change $|\tilde {\nabla }_H f|^{2}$![]() into $|\nabla _H f|^{2}$
into $|\nabla _H f|^{2}$![]() . In view of (4.8), when $\mathbb {G}$
. In view of (4.8), when $\mathbb {G}$![]() is of Heisenberg type we obtain from (4.7)
is of Heisenberg type we obtain from (4.7)

but it is not true that the right-hand side of (4.9) generically vanishes when $h\not = k$![]() . This lack of orthogonality of the spherical harmonics causes the nondecreasing monotonicity of the frequency (4.1) to fail for a harmonic function of the type $f = P_h + P_k$
. This lack of orthogonality of the spherical harmonics causes the nondecreasing monotonicity of the frequency (4.1) to fail for a harmonic function of the type $f = P_h + P_k$![]() . As a consequence, one cannot expect an Almgren type monotonicity formula on a generic harmonic function $f$
. As a consequence, one cannot expect an Almgren type monotonicity formula on a generic harmonic function $f$![]() , unless additional assumptions are imposed on $f$
, unless additional assumptions are imposed on $f$![]() itself.
itself.
We close by illustrating this claim. Suppose that $\mathbb {G} = \mathbb {H}^{1}$![]() and consider either one of the harmonic functions in $\mathbb {H}^{1}$
and consider either one of the harmonic functions in $\mathbb {H}^{1}$![]() given in (1.14) or (1.21). If to fix the ideas we consider (1.21), since $f = P_1 + P_3$
given in (1.14) or (1.21). If to fix the ideas we consider (1.21), since $f = P_1 + P_3$![]() , where $P_1(x,\,y,\,\sigma ) = x$
, where $P_1(x,\,y,\,\sigma ) = x$![]() and $P_3(x,\,y,\,\sigma ) = 6 y \sigma - x^{3}$
and $P_3(x,\,y,\,\sigma ) = 6 y \sigma - x^{3}$![]() , with $Z = x \partial _x + y \partial _y + 2 \sigma \partial _\sigma$
, with $Z = x \partial _x + y \partial _y + 2 \sigma \partial _\sigma$![]() we presently have $Z P_1 = P_1$
we presently have $Z P_1 = P_1$![]() , $Z P_3 = 3 P_3$
, $Z P_3 = 3 P_3$![]() . As a consequence, (4.5) gives
. As a consequence, (4.5) gives

where we have let

Observe now that
and
Now notice that $P_1 P_3 = 6 xy \sigma - x^{4}$![]() . Since $xy \sigma$
. Since $xy \sigma$![]() is odd, if we set
is odd, if we set
then $a,\, b,\, c >0$![]() , and we have from (4.10)
, and we have from (4.10)
A simple calculation gives
provided that $0\le r\le r_0$![]() , for some $r_0>0$
, for some $r_0>0$![]() sufficiently small. Therefore, $r\to N(f,\,r)$
sufficiently small. Therefore, $r\to N(f,\,r)$![]() is nonincreasing on $(0,\,r_0)$
is nonincreasing on $(0,\,r_0)$![]() , instead on nondecreasing!
, instead on nondecreasing!
Acknowledgments
The author is supported in part by a Progetto SID: ‘Non-local Sobolev and isoperimetric inequalities’, University of Padova, 2019.