Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T03:00:16.312Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on lower limit of series and potential theory

Published online by Cambridge University Press:  14 November 2011

N. Chevallier
N. Chevallier
Affiliation:
Université de haute Alsace, F.S.T., 4 rue des fréres lumière, 68093 Mulhouse Cedex, France
Get access Rights & Permissions [Opens in a new window]

Synopsis

We are looking for positive sequences (bn) which have the following property: If (an) is a positive sequence such that 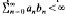, then

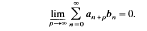
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 121 , Issue 3-4 , 1992 , pp. 273 - 277
Copyright
Copyright © Royal Society of Edinburgh 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Kaluza, Th.. Uber die Koeffizienten reziproker Potenzreihen. Math. Z. 23 (1928), 000–000.Google Scholar
2Korany, A. and Taylor, J. C.. Fine convergence and parabolic convergence for the Helmoltz equation and heat equation. Illinois J. Math. 27 (1983), 77–93.Google Scholar
3Doob, J. L.. Classical Potential Theory and its Probabilistic Counterpart (Berlin: Springer, 1983).Google Scholar