Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T01:53:02.941Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on a positive solution of a null mass nonlinear field equation in exterior domains

Part of: Equations of mathematical physics and other areas of application Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  26 January 2019

Alireza Khatib  and
Liliane A. Maia
Alireza Khatib
Affiliation:
Departamento de Matemática, Universidade Federal do Amazonas, Manaus, Amazonas, 69077-000, Brazil ([email protected])
Liliane A. Maia
Affiliation:
Departamento de Matemática, Universidade de Brasília, Brasília-DF, 70910-900, Brazil ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Null Mass nonlinear field equation (𝒫)

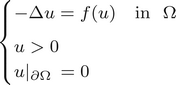$$\left\{ {\matrix{ {-\Delta u = f(u){\rm in}\;\;\Omega } \hfill \hfill \hfill \hfill \cr {u > 0} \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \hfill \cr {u \vert_{\partial \Omega } = 0} \cr } } \right.$$
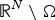where ${\open R}^N \setminus \Omega $ is a bounded regular domain. The existence of a bound state solution is established in situations where this problem does not have a ground state.

Keywords

Nonlinear null mass equationexterior domainvariational methods

MSC classification

Primary: 35Q55: NLS-like equations (nonlinear Schrödinger)
Secondary: 35J20: Variational methods for second-order elliptic equations 35B09: Positive solutions
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 841 - 870
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Azzollini, A., Benci, V., D'Aprile, T. and Fortunato, D.. Existence of static solutions of the semilinear Maxwell equations. Ricerche di Matematica 55 (2006), 283–296.CrossRefGoogle Scholar
2Badiale, M., Pisani, L. and Rolando, S.. Sum of weighted Lebesgue spaces and nonlinear elliptic equations. Nonlinear Differ. Equ. Appl. 18 (2011), 369–405.CrossRefGoogle Scholar
3Bartsch, T. and Weth, T.. Three nodal solutions of singularly elliptic equations on domains without topology. Ann. I. H. Poincaré Anal. Non Linéaire 22 (2005), 259–281.CrossRefGoogle Scholar
4Benci, V. and Cerami, G.. Positive solutions of some nonlinear elliptic problems in exterior domains. Arch. Rational Mech. Anal. 99 (1987), 283–300.CrossRefGoogle Scholar
5Benci, V. and Fortunato, D.. A strongly degenerate elliptic equation arising from the semilinear Maxwell equations. C. R. Acad. Sci. Paris serie I. 339 (2004a), 839–842.CrossRefGoogle Scholar
6Benci, V. and Fortunato, D.. Towards a unified field theory for classical electrodynamics. Arch. Rational Mech. Anal. 173 (2004b), 379–414.CrossRefGoogle Scholar
7Benci, V. and Micheletti, A. M.. Solutions in exterior domains of null mass nonlinear field equations. Adv. Nonlin. Stud. 6 (2006), 171–198.CrossRefGoogle Scholar
8Berestycki, H. and Lions, P.-L.. Nonlinear scalar field equations. I. Existence of a ground state. Arch. Rational Mech. Anal. 82 (1983a), 313–345.CrossRefGoogle Scholar
9Berestycki, H. and Lions, P.-L.. Nonlinear scalar field equations. II. Existence of a ground state. Arch. Rational Mech. Anal. 82 (1983b), 347–376.CrossRefGoogle Scholar
10Berg, J. and Lofstrom, J.. Interpolation spaces (Berlin, Heidelberg, New York: Springer Verlag, 1976).CrossRefGoogle Scholar
11Bonnet, A.. A deformation lemma on C 1 manifold. Manuscripta Math 81 (1993), 339–359.CrossRefGoogle Scholar
12Caffarelli, L. A., Gidas, B. and Spruck, J.. Asymptotic symmetry and local behavior of semilinear elliptic equations with critical Sobolev growth. Comm. Pure Appl. Math. 42 (1989), 271–297.CrossRefGoogle Scholar
13Cerami, G. and Passaseo, D.. Existence and multiplicity results for semi linear elliptic dirichlet problems in exterior domains. Nonlin. Anal. TMA 24Google Scholar
14Clapp, M. and Maia, L. A.. A positive bound state for an asymptotically linear or superlinear Schrödinger equation. J. Differ. Equ. 260 (2016), 3173–3192.CrossRefGoogle Scholar
15Clapp, M. and Maia, L. A.. Existence of a positive solution to a nonlinear scalar field equation with zero mass at infinity. Adv. Nonlinear Stud. 18 (2018), 745–762.CrossRefGoogle Scholar
16Dautray, R. and Lions, J.-L.. Mathematical analysis and numerical methods for science and technology. In Physical origins and classical methods, vol. 1, pp. xviii+695 (Berlin: Springer-Verlag, 1990).Google Scholar
17Esteban, M. J. and Lions, P. L.. Existence and non-existence results for semilinear elliptic problems in unbounded domains. Proc. Royal Edinbourgh Soc. 93 (1982), 1–14.CrossRefGoogle Scholar
18Gidas, B.. Bifurcation phenomena in mathematical physics and related topics (eds. Bardos, C. and Bessis, D.). (Dordrecht, Holland: Reidel, 1980).Google Scholar
19Lions, P. L.. The concentration-compactness principle in the calculus of variations. The locally compact case. Ann. I. H. Poincaré, A. N. 1 (1984), 109–145 and 223–283.CrossRefGoogle Scholar
20Maia, L. A. and Pellacci, B.. Positive solutions for asymptotically linear problems in exterior domains. Annali di Matematica Pura ed Applicata 196 (2017), 1399–1430.CrossRefGoogle Scholar
21Strauss, W. A.. Existence of solitary waves in higher dimensions. Comm. Math. Phys. 55 (1977), 149–162.CrossRefGoogle Scholar
22Strauss, W. A. and Vázquez, L.. Existence of localized solutions for certain model field theories. J. Math. Phys. 22 (1981), 1005–1009.CrossRefGoogle Scholar
23Struwe, M.. A global compactness result for elliptic boundary value problems involving limiting nonlinearities. Math. Z. 187 (1984), 511–517.CrossRefGoogle Scholar
24Vétois, J.. A priori estimates and application to the symmetry of solutions for critical p-Laplace equations. J. Differ. Equ. 260 (2016), 149–161.CrossRefGoogle Scholar
25Willem, M.. Minimax theorems, progress in nonlinear differential equations and their applications, vol. 24 (Boston, MA: Birkhauser Boston, Inc., 1996).Google Scholar