Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-22T23:04:01.902Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonsingular bilinear maps revisited

Part of: Forms and linear algebraic groups Topological manifolds

Published online by Cambridge University Press:  17 March 2020

Carlos Domínguez  and
Kee Yuen Lam
Carlos Domínguez
Affiliation:
Académia de Matemáticas, Unidad Interdisciplinaria de Ingeniería Campus Guanajuato, Institúto Politécnico Nacional, Av. Mineral de Valenciana 200, Fracc. Industrial Puerto Interior, Silao de la Victoria, GuanajuatoC. P.36275, México ([email protected])
Kee Yuen Lam
Affiliation:
Department of Mathematics, University of British Columbia, VancouverB.C., V6T 1Z2, Canada ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

A bilinear map 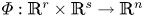$\varPhi :\mathbb {R}^r\times \mathbb {R}^s\to \mathbb {R}^n$ is nonsingular if 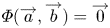$\varPhi (\overrightarrow {a},\overrightarrow {b})=\overrightarrow {0}$ implies 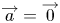$\overrightarrow {a}=\overrightarrow {0}$ or 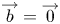$\overrightarrow {b}=\overrightarrow {0}$. These maps are of interest to topologists, and are instrumental for the study of vector bundles over real projective spaces. The main purpose of this paper is to produce examples of such maps in the range 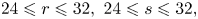$24\leqslant r\leqslant 32,\ 24\leqslant s\leqslant 32,$ using the arithmetic of octonions (otherwise known as Cayley numbers) as an effective tool. While previous constructions in lower dimensional cases use ad hoc techniques, our construction follows a systematic procedure and subsumes those techniques into a uniform perspective.

Keywords

Bilinear mapsPolynomial productImmersionVector bundlesProjective spaces

MSC classification

Primary: 57N35: Embeddings and immersions
Secondary: 11E39: Bilinear and Hermitian forms
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 1 , February 2021 , pp. 377 - 390
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Adem, J.. Some immersions associated with bilinear maps. Bol. Soc. Mat. Mex. 13 (1968), 95–104.Google Scholar
2Adem, J., On nonsingular bilinear maps. In The steenrod algebra and its applications, ed. Peterson, F. P.. Lecture Notes in Math., vol. 168, pp. 11–24 (Berlin-Heidelberg, New York: Springer-Verlag, 1970).Google Scholar
3Adem, J.. On nonsingular bilinear maps II. Bol. Soc. Mat. Mex. 16 (1971), 64–70.Google Scholar
4Ginsburg, M.. Some immersions of projective space in Euclidean space. Topology 2 (1963), 69–71.CrossRefGoogle Scholar
5Hopf, H.. Ein topologischer Beitrag zur reellen Algebra. Comment Math. Helv. 13 (1941), 219–239.CrossRefGoogle Scholar
6Kitchloo, N. and Wilson, S.. The second real Johnson-Wilson theory and non-immersions of $\mathbb {R} P^n$, Homology. Homotopy Appl. 10 (2008), 223–268.CrossRefGoogle Scholar
7Lam, K. Y.. Construction of nonsingular bilinear maps. Topology 6 (1967), 423–426.CrossRefGoogle Scholar
8Lam, K. Y.. Construction of some nonsingular bilinear maps. Bol. Soc. Mat. Mex. (2) 13 (1968), 88–94.Google Scholar
9Lam, K. Y.. On bilinear and skew-linear maps that are nonsingular. Quart. J. Math. Oxford (2) 19 (1968), 281–288.CrossRefGoogle Scholar
10Lam, K. Y.. Nonsingular bilinear maps and stable homotopy classes of spheres. Math. Proc. Cambridge Philos. Soc. 82 (1977), 419–425.CrossRefGoogle Scholar
11Lam, K. Y., Borsuk-ulam type theorems and systems of bilinear equations. Geometry from the Pacfic Rim, pp. 183–194 (Berlin-New York, Walter de Gruyer, 1997).Google Scholar
12Milgram, J.. Immersing projective spaces. Ann. Math. 85 (1967), 473–482.CrossRefGoogle Scholar
13Rees, E. G.. Linear spaces of real matrices of large rank. Proc. R. Soc. Edinburgh Sect. A 126 (1996), 147–151.CrossRefGoogle Scholar
14Steer, B.. On the Embedding of projective spaces in euclidean space. Proc. London Math. Soc. (3) 21 (1970), 489–501.CrossRefGoogle Scholar
15Stiefel, E.. Uber Richtungsfelder in den projektiven Raumen und einen Satz aus der reellen Algebra. Comment Math. Helv. 13 (1941), 201–208.CrossRefGoogle Scholar