Published online by Cambridge University Press: 24 July 2014
The theory of closed sesquilinear forms in the non-semi-bounded situation exhibits some new features, as opposed to the semi-bounded situation. In particular, there can be more than one closed form associated with the generalized Friedrichs extension SF of a non-semi-bounded symmetric operator S (if SF exists). However, there is one unique form 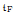 [·, ·] satisfying Kato's second representation theorem and, in particular, dom
[·, ·] satisfying Kato's second representation theorem and, in particular, dom 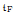 = dom ∣SF∣1/2. In the present paper, another closed form
= dom ∣SF∣1/2. In the present paper, another closed form 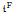 [·, ·], also uniquely associated with SF, is constructed. The relation between these two forms is analysed and it is shown that these two non-semi-bounded forms can indeed differ from each other. Some general criteria for their equality are established. The results induce solutions to some open problems concerning generalized Friedrichs extensions and complete some earlier results about them in the literature. The study is connected to the spectral functions of definitizable operators in Kreĭn spaces.
[·, ·], also uniquely associated with SF, is constructed. The relation between these two forms is analysed and it is shown that these two non-semi-bounded forms can indeed differ from each other. Some general criteria for their equality are established. The results induce solutions to some open problems concerning generalized Friedrichs extensions and complete some earlier results about them in the literature. The study is connected to the spectral functions of definitizable operators in Kreĭn spaces.