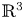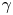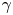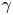1. Introduction and main results
Developable, or flat, surfaces in $\mathbb {R}^{3}$![]() are among the most classical and well-studied objects in differential geometry [Reference Lawrence15, Reference Ushakov26]. They are characterized by having zero Gaussian curvature or, equivalently, by being ruled surfaces with a constant family of tangent planes along each ruling. Our main interest in this article is to study the set of flat surfaces containing a given space curve, or, more precisely, the set of flat ribbons along $\gamma$
are among the most classical and well-studied objects in differential geometry [Reference Lawrence15, Reference Ushakov26]. They are characterized by having zero Gaussian curvature or, equivalently, by being ruled surfaces with a constant family of tangent planes along each ruling. Our main interest in this article is to study the set of flat surfaces containing a given space curve, or, more precisely, the set of flat ribbons along $\gamma$![]() .
.
Let $I =[0,\,L]$![]() , let $\gamma \colon I \to \mathbb {R}^{3}$
, let $\gamma \colon I \to \mathbb {R}^{3}$![]() be a smooth, regular connected curve, and let $S \subset \mathbb {R}^{3}$
be a smooth, regular connected curve, and let $S \subset \mathbb {R}^{3}$![]() be a smooth surface; without loss of generality, we may assume $\gamma$
be a smooth surface; without loss of generality, we may assume $\gamma$![]() to be unit-speed. We say that $S$
to be unit-speed. We say that $S$![]() is locally nonplanar if it does not contain any planar open set. Furthermore, if $S$
is locally nonplanar if it does not contain any planar open set. Furthermore, if $S$![]() is ruled and $\gamma (t) \in S$
is ruled and $\gamma (t) \in S$![]() , then we define the width of $S$
, then we define the width of $S$![]() (with respect to $\gamma$
(with respect to $\gamma$![]() ) at $t$
) at $t$![]() to be the length of the projection of the ruling passing from $\gamma (t)$
to be the length of the projection of the ruling passing from $\gamma (t)$![]() onto the normal plane $\gamma '(t)^{\perp }$
onto the normal plane $\gamma '(t)^{\perp }$![]() .
.
Definition 1 A developable surface $D$![]() that contains $\gamma$
that contains $\gamma$![]() is called a flat ribbon along $\gamma$
is called a flat ribbon along $\gamma$![]() if the following conditions are satisfied:
if the following conditions are satisfied:
(1) $D$
 is locally nonplanar, and it is a compact subset of $\mathbb {R}^{3}$
is locally nonplanar, and it is a compact subset of $\mathbb {R}^{3}$ .
.(2) $\gamma$
 is transversal to every ruling of $D$
is transversal to every ruling of $D$ and meets each of them at the midpoint.
and meets each of them at the midpoint.(3) $D$
 has constant width.
has constant width.
It is well known that, if the curvature of $\gamma$![]() is always different from zero, then there exist plenty of flat ribbons along $\gamma$
is always different from zero, then there exist plenty of flat ribbons along $\gamma$![]() . Indeed, let $N \colon I \to \mathbb {R}^{3}$
. Indeed, let $N \colon I \to \mathbb {R}^{3}$![]() be a unit vector field – always normal to $\gamma '$
be a unit vector field – always normal to $\gamma '$![]() – along $\gamma$
– along $\gamma$![]() . It is not difficult to check that, if $\langle \gamma ''(t),\, N(t) \rangle \neq 0$
. It is not difficult to check that, if $\langle \gamma ''(t),\, N(t) \rangle \neq 0$![]() for all $t \in I$
for all $t \in I$![]() , then the image of the map $t \mapsto \gamma (t) + (N(t)^{\perp } \cap N'(t)^{\perp })$
, then the image of the map $t \mapsto \gamma (t) + (N(t)^{\perp } \cap N'(t)^{\perp })$![]() is a well-defined surface in a neighbourhood of $\gamma$
is a well-defined surface in a neighbourhood of $\gamma$![]() , both locally nonplanar and flat; see [Reference do Carmo5, pp. 195–197] and § 3.
, both locally nonplanar and flat; see [Reference do Carmo5, pp. 195–197] and § 3.
On the other hand, to any (singly) ruled surface containing $\gamma$![]() one can associate a function $\alpha \colon I \to [0,\,\pi )$
one can associate a function $\alpha \colon I \to [0,\,\pi )$![]() , called ruling angle, describing the angle between the ruling line and the tangent vector of $\gamma$
, called ruling angle, describing the angle between the ruling line and the tangent vector of $\gamma$![]() . Different ruled surfaces along $\gamma$
. Different ruled surfaces along $\gamma$![]() possessing equal ruling angle could/should be regarded as akin, if not equivalent.
possessing equal ruling angle could/should be regarded as akin, if not equivalent.
It is therefore natural to consider the following problem.
Problem 2 Given a flat ribbon along $\gamma$![]() , describe the set of all flat ribbons along the same curve $\gamma$
, describe the set of all flat ribbons along the same curve $\gamma$![]() having the given width and ruling angle.
having the given width and ruling angle.
In this paper, we shall see that, under some mild conditions, the set in question is isomorphic to a full circle. Indeed, suppose that $N$![]() is the normal vector of a flat ribbon $\mathcal {R}(N)$
is the normal vector of a flat ribbon $\mathcal {R}(N)$![]() along $\gamma$
along $\gamma$![]() , and denote the corresponding ruling angle by $\alpha (N)$
, and denote the corresponding ruling angle by $\alpha (N)$![]() . Then the following result holds.
. Then the following result holds.
Theorem 3 Suppose that $\gamma$![]() is locally nonplanar, i.e., its restriction to any open interval is nonplanar, and let $\varphi$
is locally nonplanar, i.e., its restriction to any open interval is nonplanar, and let $\varphi$![]() be a smooth function $I \to (0,\, \pi )$
be a smooth function $I \to (0,\, \pi )$![]() . For any $t_{0} \in I$
. For any $t_{0} \in I$![]() and any unit vector $v \in \gamma '(t_{0})^{\perp },$
and any unit vector $v \in \gamma '(t_{0})^{\perp },$![]() there exists a flat ribbon $\mathcal {R}(V)$
there exists a flat ribbon $\mathcal {R}(V)$![]() along $\gamma$
along $\gamma$![]() such that $V(t_{0})=v$
such that $V(t_{0})=v$![]() and $\alpha (V) = \varphi$
and $\alpha (V) = \varphi$![]() .
.
Corollary 4 Suppose that $\gamma$![]() is locally nonplanar, and let $\mathcal {R}(N)$
is locally nonplanar, and let $\mathcal {R}(N)$![]() be a flat ribbon along $\gamma$
be a flat ribbon along $\gamma$![]() . For any $t_{0} \in I$
. For any $t_{0} \in I$![]() and any unit vector $v \in \gamma '(t_{0})^{\perp },$
and any unit vector $v \in \gamma '(t_{0})^{\perp },$![]() there exists a flat ribbon $\mathcal {R}(V)$
there exists a flat ribbon $\mathcal {R}(V)$![]() along $\gamma,$
along $\gamma,$![]() having the same width as $\mathcal {R}(N),$
having the same width as $\mathcal {R}(N),$![]() such that $V(t_{0})=v$
such that $V(t_{0})=v$![]() and $\alpha (V) = \alpha (N)$
and $\alpha (V) = \alpha (N)$![]() .
.
Corollary 5 Suppose that $\gamma$![]() is locally nonplanar. The set of all flat ribbons of any fixed width along $\gamma$
is locally nonplanar. The set of all flat ribbons of any fixed width along $\gamma$![]() admitting a smooth asymptotic parametrization is isomorphic to $C^{\infty }(I; (0,\,\pi )) \times \mathbb {S}^{1}$
admitting a smooth asymptotic parametrization is isomorphic to $C^{\infty }(I; (0,\,\pi )) \times \mathbb {S}^{1}$![]() .
.
Remark 6 The nonplanarity assumption in theorem 1.3 allows $\gamma$![]() to have isolated points of vanishing curvature or torsion. It is only needed because we have excluded a planar strip to qualify as a flat ribbon. Indeed, if $\gamma$
to have isolated points of vanishing curvature or torsion. It is only needed because we have excluded a planar strip to qualify as a flat ribbon. Indeed, if $\gamma$![]() is planar, then there exists a vector $v$
is planar, then there exists a vector $v$![]() for which the corresponding ribbon degenerates into a planar strip.
for which the corresponding ribbon degenerates into a planar strip.
Remark 7 The definition of $I$![]() as a closed interval is essential for the validity of the theorem. Suppose for a moment that $I$
as a closed interval is essential for the validity of the theorem. Suppose for a moment that $I$![]() is an arbitrary interval. Then theorem 1.3 holds provided the functions $\kappa _{g} \cot (\varphi )$
is an arbitrary interval. Then theorem 1.3 holds provided the functions $\kappa _{g} \cot (\varphi )$![]() and $\kappa _{n} \cot (\varphi )$
and $\kappa _{n} \cot (\varphi )$![]() are bounded; see § 4. Without this extra hypothesis, we could yet prove the following local statement: for any $t_{0} \in I$
are bounded; see § 4. Without this extra hypothesis, we could yet prove the following local statement: for any $t_{0} \in I$![]() and any unit vector $v \in \gamma '(t_{0})^{\perp }$
and any unit vector $v \in \gamma '(t_{0})^{\perp }$![]() , there exists a neighbourhood $I_{0}$
, there exists a neighbourhood $I_{0}$![]() of $t_{0}$
of $t_{0}$![]() and a flat ribbon $\mathcal {R}_{0}(V)$
and a flat ribbon $\mathcal {R}_{0}(V)$![]() along $\gamma \rvert _{I_{0}}$
along $\gamma \rvert _{I_{0}}$![]() such that $V(t_{0})=v$
such that $V(t_{0})=v$![]() and $\alpha _{0}(V) = \varphi \rvert _{I_{0}}$
and $\alpha _{0}(V) = \varphi \rvert _{I_{0}}$![]() .
.
Remark 8 The extra assumption in corollary 1.5 is needed because the ruling angle of a flat ribbon along $\gamma$![]() , in the presence of planar points, may fail to be differentiable in a nowhere dense set; see [Reference Ushakov25].
, in the presence of planar points, may fail to be differentiable in a nowhere dense set; see [Reference Ushakov25].
To the best of the author's knowledge, theorem 1.3 has not appeared in the literature before. This is somewhat surprising, given the classical nature of the subject and the relative simplicity of the proof.
The proof of theorem 1.3, which is based on the standard theory of ordinary differential equations, will be given in § 4. In particular, the proof offers a means to construct the solution by solving a nonlinear differential equation of first order; see figure 1.
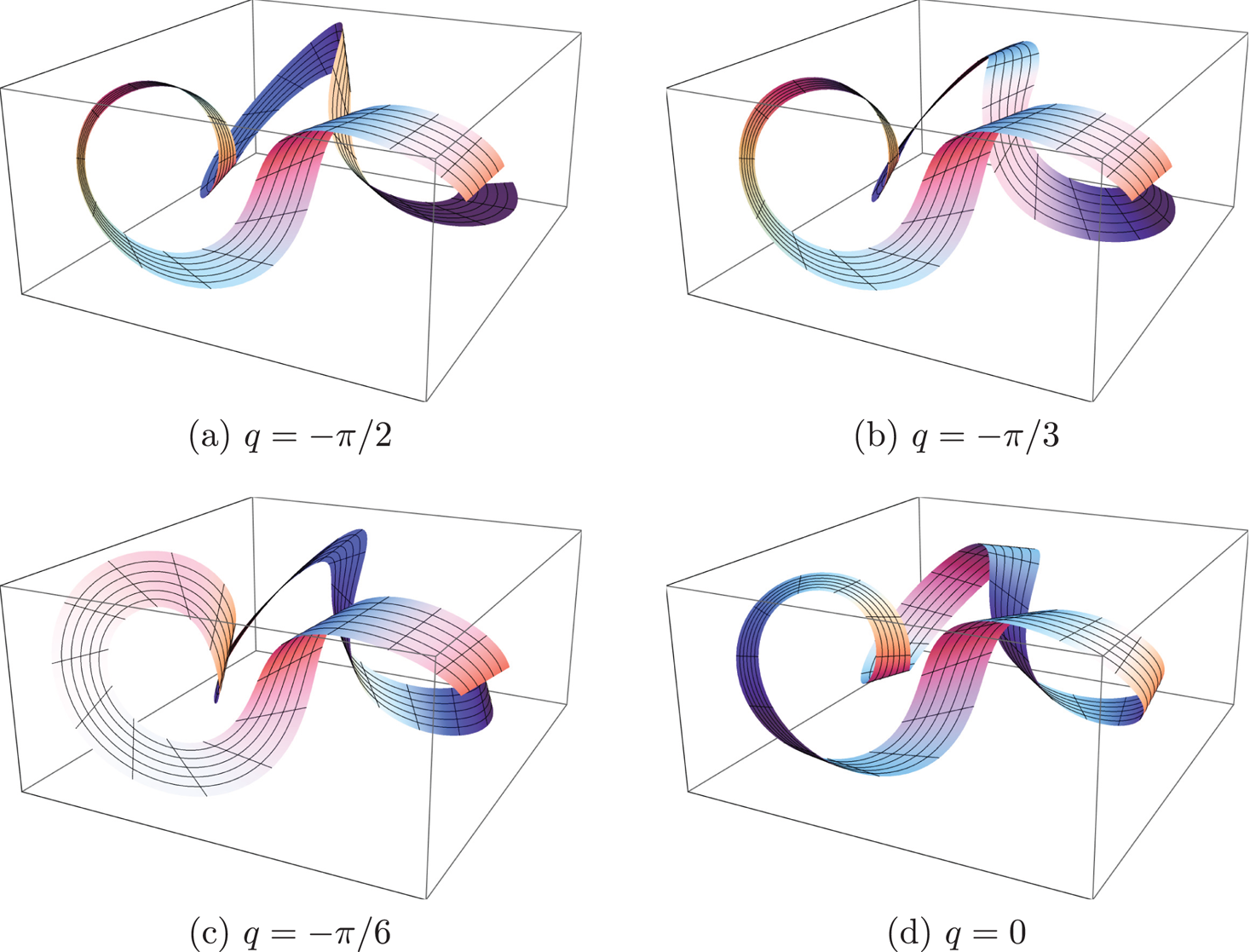
FIGURE 1. Examples of flat ribbons along $\gamma$![]() having the same width and ruling angle. The curve $\gamma \colon [0,\,2\pi ] \to \mathbb {R}^{3}$
having the same width and ruling angle. The curve $\gamma \colon [0,\,2\pi ] \to \mathbb {R}^{3}$![]() is a trivial torus knot, while the ruling angle is induced by the unit normal vector of the torus; in other words, we are considering the ruling angle of a flat ribbon that is tangent to the torus along $\gamma$
is a trivial torus knot, while the ruling angle is induced by the unit normal vector of the torus; in other words, we are considering the ruling angle of a flat ribbon that is tangent to the torus along $\gamma$![]() (shown in plot (d)). Each plot corresponds to a different initial condition $v \in \gamma '(0)^{\perp }$
(shown in plot (d)). Each plot corresponds to a different initial condition $v \in \gamma '(0)^{\perp }$![]() , obtained by rotating the normal vector of the torus at $\gamma (0)$
, obtained by rotating the normal vector of the torus at $\gamma (0)$![]() by an angle $q$
by an angle $q$![]() . Plots (a), (b) and (c) are generated by solving numerically equation (4.6). (a) $q=-\pi /2$
. Plots (a), (b) and (c) are generated by solving numerically equation (4.6). (a) $q=-\pi /2$![]() , (b) $q=-\pi /3$
, (b) $q=-\pi /3$![]() , (c) $q=-\pi /6$
, (c) $q=-\pi /6$![]() , (d) $q=0$
, (d) $q=0$![]() .
.
It is worth emphasizing that any two flat ribbons $\mathcal {R}(N_{1})$![]() and $\mathcal {R}(N_{2})$
and $\mathcal {R}(N_{2})$![]() are locally isometric, by Minding's theorem. More precisely, for any $p_{1} \in \mathcal {R}(N_{1})$
are locally isometric, by Minding's theorem. More precisely, for any $p_{1} \in \mathcal {R}(N_{1})$![]() and $p_{2} \in \mathcal {R}(N_{2})$
and $p_{2} \in \mathcal {R}(N_{2})$![]() , there exist neighbourhoods $\mathcal {U}_{1}$
, there exist neighbourhoods $\mathcal {U}_{1}$![]() of $p_{1}$
of $p_{1}$![]() , $\mathcal {U}_{2}$
, $\mathcal {U}_{2}$![]() of $p_{2}$
of $p_{2}$![]() and an isometry $\mathcal {U}_{1} \to \mathcal {U}_{2}$
and an isometry $\mathcal {U}_{1} \to \mathcal {U}_{2}$![]() . On the other hand, if $\mathcal {R}(N_{1})$
. On the other hand, if $\mathcal {R}(N_{1})$![]() and $\mathcal {R}(N_{2})$
and $\mathcal {R}(N_{2})$![]() have the same ruling angle, then in general they are not globally isometric. This can be deduced from the fact that the geodesic curvatures of $\gamma$
have the same ruling angle, then in general they are not globally isometric. This can be deduced from the fact that the geodesic curvatures of $\gamma$![]() relative to $\mathcal {R}(N_{1})$
relative to $\mathcal {R}(N_{1})$![]() and $\mathcal {R}(N_{2})$
and $\mathcal {R}(N_{2})$![]() are typically different; see remark 4.2.
are typically different; see remark 4.2.
The second objective of the paper is to understand the set of flat ribbons along $\gamma$![]() in terms of energy. In 1930, Sadowsky [Reference Hinz and Fried13, Reference Sadowsky20] argued that the bending energy $\int _{D} H^{2} \,{\rm d}A$
in terms of energy. In 1930, Sadowsky [Reference Hinz and Fried13, Reference Sadowsky20] argued that the bending energy $\int _{D} H^{2} \,{\rm d}A$![]() of the rectifying developable of $\gamma$
of the rectifying developable of $\gamma$![]() , in the limit of infinitely small width, is proportional to
, in the limit of infinitely small width, is proportional to
Here $\kappa >0$![]() is the curvature of $\gamma$
is the curvature of $\gamma$![]() and $\mu = -\tau /\kappa$
and $\mu = -\tau /\kappa$![]() , where $\tau$
, where $\tau$![]() is the torsion. Sadowsky's claim was formally justified by Wunderlich [Reference Todres24, Reference Wunderlich27].
is the torsion. Sadowsky's claim was formally justified by Wunderlich [Reference Todres24, Reference Wunderlich27].
In § 4 we will prove that Sadowsky's result extends virtually unchanged to any flat ribbon along $\gamma$![]() ; cf. [Reference Efrati6].
; cf. [Reference Efrati6].
Theorem 9 If $\mathcal {R}(N)$![]() has width $2w,$
has width $2w,$![]() then its bending energy $\mathcal {E}(\mathcal {R}(N)) =\mathcal {E}(N)$
then its bending energy $\mathcal {E}(\mathcal {R}(N)) =\mathcal {E}(N)$![]() satisfies
satisfies
where $\kappa _{n}$![]() is the normal curvature of $\gamma$
is the normal curvature of $\gamma$![]() with respect to $N,$
with respect to $N,$![]() as defined in § 2.
as defined in § 2.
Remark 10 The function $\cot (\alpha (N))$![]() agrees with $\mu = -\tau _{g}/\kappa _{n}$
agrees with $\mu = -\tau _{g}/\kappa _{n}$![]() on the subset $I \setminus \kappa _{n}^{-1}(\{0\})$
on the subset $I \setminus \kappa _{n}^{-1}(\{0\})$![]() , which is dense in $I$
, which is dense in $I$![]() ; here $\tau _{g}$
; here $\tau _{g}$![]() is the geodesic torsion of $\gamma$
is the geodesic torsion of $\gamma$![]() with respect to $N$
with respect to $N$![]() . Thus $\cot (\alpha (N))$
. Thus $\cot (\alpha (N))$![]() is the unique continuous extension of $\mu$
is the unique continuous extension of $\mu$![]() to $I$
to $I$![]() .
.
Theorem 1.9 tells us that, for any ruling angle, the ribbon in which $\gamma$![]() has the least energy ($=\int _{0}^{L}\kappa _{g}^{2}\,{\rm d}t$
has the least energy ($=\int _{0}^{L}\kappa _{g}^{2}\,{\rm d}t$![]() , where $\kappa _{g}$
, where $\kappa _{g}$![]() is the geodesic curvature of $\gamma$
is the geodesic curvature of $\gamma$![]() with respect to $N$
with respect to $N$![]() ) costs the most energy, and vice versa. Hence when $\kappa > 0$
) costs the most energy, and vice versa. Hence when $\kappa > 0$![]() we obtain: among all infinitely narrow flat ribbons along $\gamma$
we obtain: among all infinitely narrow flat ribbons along $\gamma$![]() having ruling angle $\alpha (T'/\lVert T'\rVert )$
having ruling angle $\alpha (T'/\lVert T'\rVert )$![]() , the rectifying developable of $\gamma$
, the rectifying developable of $\gamma$![]() has the maximum bending energy.
has the maximum bending energy.
More generally, the following corollary applies.
Corollary 11 If $\mathcal {R}(N)$![]() and $\mathcal {R}(V)$
and $\mathcal {R}(V)$![]() are flat ribbons along $\gamma$
are flat ribbons along $\gamma$![]() with the same ruling angle, then, in the limit of infinitely small widths, their bending energies $\mathcal {E}(N)$
with the same ruling angle, then, in the limit of infinitely small widths, their bending energies $\mathcal {E}(N)$![]() and $\mathcal {E}(V)$
and $\mathcal {E}(V)$![]() satisfy
satisfy
where $\kappa _{g}$![]() is the geodesic curvature of $\gamma$
is the geodesic curvature of $\gamma$![]() with respect to $N$
with respect to $N$![]() , as defined in § 2. In particular, if the normal curvature $\kappa _{n}$
, as defined in § 2. In particular, if the normal curvature $\kappa _{n}$![]() of $\gamma$
of $\gamma$![]() with respect to $N$
with respect to $N$![]() is always nonzero, then
is always nonzero, then
where $\rho = \kappa _{g}/\kappa _{n}$![]() and $\phi$
and $\phi$![]() is the angle between $N$
is the angle between $N$![]() and $\gamma ''$
and $\gamma ''$![]() .
.
The plan of the paper is as follows. The next two sections present the preliminaries needed for the proof of theorem 1.3, which is carried out in § 4. In § 5 we then proceed with the proofs of theorem 1.9 and corollary 1.11. In the subsequent section we derive further results by considering two natural choices of ruling angle. Finally, in § 7 we specialize the discussion to the case where the curve $\gamma$![]() is a circular helix.
is a circular helix.
This work joins several other recent studies on ribbons; see e.g. [Reference Bohr and Markvorsen2, Reference Fosdick and Fried7, Reference Freddi, Hornung, Mora and Paroni8, Reference Seguin, Chen and Fried21]. In particular, the problem of constructing flat surfaces along a given curve has also been considered in [Reference Hananoi and Izumiya12, Reference Izumiya and Otani14, Reference Raffaelli, Bohr and Markvorsen18, Reference Zhao and Wang28]; interesting applications of Sadowsky's energy formula can be found in [Reference Chubelaschwili and Pinkall3, Reference Dias and Audoly4, Reference Giomi and Mahadevan11, Reference Starostin and van der Heijden23].
In fact, a closely related work [Reference Seguin, Chen and Fried22] appeared shortly before the first version of this paper was completed. By basing their analysis on the geodesic curvature – rather than the ruling angle – the authors in [Reference Seguin, Chen and Fried22] offer an alternative description of the surfaces studied here.
2. The Darboux frame
We begin by defining the Darboux frame. Classically, that is a natural frame along a surface curve. For our purposes, the surface is not important, only the normal vector is.
Let $N$![]() be a (smooth) unit normal vector field along $\gamma$
be a (smooth) unit normal vector field along $\gamma$![]() , let $T$
, let $T$![]() be the unit tangent vector $\gamma '$
be the unit tangent vector $\gamma '$![]() of $\gamma$
of $\gamma$![]() , and let $H=N\times T$
, and let $H=N\times T$![]() . We define
. We define
• the Darboux frame of $\gamma$
 with respect to $N$
with respect to $N$ to be the triple $(T,\, H,\, N)$
to be the triple $(T,\, H,\, N)$ ;
;• the geodesic curvature $\kappa _{g}$
 of $\gamma$
of $\gamma$ with respect to $N$
with respect to $N$ by $\kappa _{g} = \langle T',\, H \rangle$
by $\kappa _{g} = \langle T',\, H \rangle$ ;
;• the normal curvature $\kappa _{n}$
 of $\gamma$
of $\gamma$ with respect to $N$
with respect to $N$ by $\kappa _{n} = \langle T',\, N \rangle$
by $\kappa _{n} = \langle T',\, N \rangle$ ;
;• the geodesic torsion $\tau _{g}$
 of $\gamma$
of $\gamma$ with respect to $N$
with respect to $N$ by $\tau _{g} = \langle H',\, N \rangle$
by $\tau _{g} = \langle H',\, N \rangle$ .
.
Since $(T,\,H,\,N)$![]() is a frame along $\gamma$
is a frame along $\gamma$![]() , we may express the derivative of any of its elements in terms of the frame itself. In fact, being $(T,\,H,\,N)$
, we may express the derivative of any of its elements in terms of the frame itself. In fact, being $(T,\,H,\,N)$![]() orthonormal, it is easy to verify that the following equations hold:
orthonormal, it is easy to verify that the following equations hold:
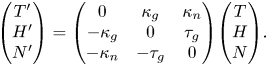
3. Constructing a flat ribbon
The Darboux frame is a useful tool for constructing a flat ribbon normal to $N$![]() along $\gamma$
along $\gamma$![]() , in that it permits to prescribe its width, which by definition is measured along the vector field $H$
, in that it permits to prescribe its width, which by definition is measured along the vector field $H$![]() .
.
Theorem 12 [Reference do Carmo5, pp. 195–197], [Reference Izumiya and Otani14, Reference Raffaelli, Bohr and Markvorsen18]
Suppose that $\kappa _{n}(t) \neq 0$![]() for all $t\in I$
for all $t\in I$![]() . Then there exists $w>0$
. Then there exists $w>0$![]() and a unique flat ribbon of width $2w$
and a unique flat ribbon of width $2w$![]() normal to $N$
normal to $N$![]() along $\gamma$
along $\gamma$![]() . Such ribbon is parametrized by $\sigma \colon I \times [-w,\,w] \to \mathbb {R}^{3},$
. Such ribbon is parametrized by $\sigma \colon I \times [-w,\,w] \to \mathbb {R}^{3},$![]()
where $\mu =-\tau _{g}/\kappa _{n}$![]() . Conversely, if $\mathcal {R}(N)$
. Conversely, if $\mathcal {R}(N)$![]() is a flat ribbon normal to $N$
is a flat ribbon normal to $N$![]() along $\gamma,$
along $\gamma,$![]() then $\tau _{g}(t) = 0$
then $\tau _{g}(t) = 0$![]() for all $t \in I$
for all $t \in I$![]() such that $\kappa _{n}(t)=0$
such that $\kappa _{n}(t)=0$![]() .
.
For the reader's convenience, we give a short proof of the theorem.
Proof of theorem 12. Proof of Theorem 3.1
Given a vector field $X$![]() along $\gamma$
along $\gamma$![]() , let $\sigma$
, let $\sigma$![]() be defined by
be defined by
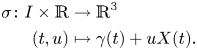
Recall that $\sigma$![]() is flat exactly when $T$
is flat exactly when $T$![]() , $X$
, $X$![]() and $X'$
and $X'$![]() are everywhere linearly dependent; accordingly, we need to find $X$
are everywhere linearly dependent; accordingly, we need to find $X$![]() such that
such that
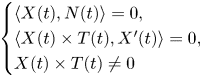
for all $t \in I$![]() . Note that the first two equations are equivalent to $X(t) \in N(t)^{\perp } \cap N'(t)^{\perp }$
. Note that the first two equations are equivalent to $X(t) \in N(t)^{\perp } \cap N'(t)^{\perp }$![]() .
.
Suppose that $\kappa _{n}(t) \neq 0$![]() . Then $N'(t) = -\kappa _{n}(t)T(t) -\tau _{g}(t)H(t) \neq 0$
. Then $N'(t) = -\kappa _{n}(t)T(t) -\tau _{g}(t)H(t) \neq 0$![]() ; the intersection $N(t)^{\perp } \cap N'(t)^{\perp }$
; the intersection $N(t)^{\perp } \cap N'(t)^{\perp }$![]() has dimension one and is spanned by
has dimension one and is spanned by
as desired.
Conversely, suppose that $\mathcal {R}(N)$![]() is a flat ribbon normal to $N$
is a flat ribbon normal to $N$![]() along $\gamma$
along $\gamma$![]() . Then $\mathcal {R}(N)$
. Then $\mathcal {R}(N)$![]() lies in the image of $\sigma$
lies in the image of $\sigma$![]() for some $X$
for some $X$![]() satisfying (3.1). Hence $\tau _{g}(t) = 0$
satisfying (3.1). Hence $\tau _{g}(t) = 0$![]() whenever $\kappa _{n}(t) =0$
whenever $\kappa _{n}(t) =0$![]() , because otherwise $\mathcal {R}(N)$
, because otherwise $\mathcal {R}(N)$![]() would be singular at $\gamma (t)$
would be singular at $\gamma (t)$![]() .
.
Remark 13 If $\kappa _{n}(t) \neq 0$![]() , then the ruling angle $\alpha (N)$
, then the ruling angle $\alpha (N)$![]() of $\mathcal {R}(N)$
of $\mathcal {R}(N)$![]() satisfies
satisfies
Remark 14 In the spirit of [ Reference Nomizu16, Reference Randrup and Røgen19], the existence condition in theorem 3.1 can be weakened as follows. For all $t \in I$![]() , we require that
, we require that
(i) there exists $l \in \mathbb {N}_{0}$
 such that the $l$
such that the $l$ th derivative $\kappa _{n}^{(l)}$
th derivative $\kappa _{n}^{(l)}$ is nonzero at $t$
is nonzero at $t$ . This implies, in particular, that every zero of $\kappa _{n}$
. This implies, in particular, that every zero of $\kappa _{n}$ is isolated;
is isolated;(ii) $\tau _{g}^{(0)}(t) = \dotsb = \tau _{g}^{(l-1)}(t) = 0$
 .
.
These two conditions guarantee that, if $\kappa _{n}(t)=0$![]() , then $\lim _{z\to t} \tau _{g}(z)/\kappa _{n}(z)$
, then $\lim _{z\to t} \tau _{g}(z)/\kappa _{n}(z)$![]() is well-defined. In fact, it is not difficult to verify that the continuous extension of $\tau _{g}/\kappa _{n}$
is well-defined. In fact, it is not difficult to verify that the continuous extension of $\tau _{g}/\kappa _{n}$![]() to $I$
to $I$![]() – obtained by setting $\tau _{g}(t)/\kappa _{n}(t) =\lim _{z\to t} \tau _{g}(z)/\kappa _{n}(z)$
– obtained by setting $\tau _{g}(t)/\kappa _{n}(t) =\lim _{z\to t} \tau _{g}(z)/\kappa _{n}(z)$![]() whenever $\kappa _{n}(t)=0$
whenever $\kappa _{n}(t)=0$![]() – is smooth.
– is smooth.
4. Proof of theorem 1.3
We are now ready to prove theorem 1.3.
Given any unit normal vector field $N$![]() along $\gamma$
along $\gamma$![]() , let the Darboux frame of $\gamma$
, let the Darboux frame of $\gamma$![]() with respect to $N$
with respect to $N$![]() rotate around the tangent $T$
rotate around the tangent $T$![]() by a smooth function $\theta \colon I \to \mathbb {R}$
by a smooth function $\theta \colon I \to \mathbb {R}$![]() :
:
The normal curvature of $\gamma$![]() with respect to $N(\theta )$
with respect to $N(\theta )$![]() is given by
is given by
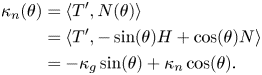
Similarly, the geodesic torsion of $\gamma$![]() with respect to $N(\theta )$
with respect to $N(\theta )$![]() is given by
is given by
We first compute
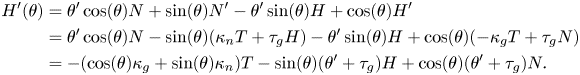
Let us also compute
and
It follows that
Next, let $\varphi$![]() be a smooth function $I \to (0,\,\pi )$
be a smooth function $I \to (0,\,\pi )$![]() , and assume that $\gamma$
, and assume that $\gamma$![]() is locally nonplanar. We claim that, if the condition
is locally nonplanar. We claim that, if the condition
holds, then the ribbon $\mathcal {R}(N(\theta ))$![]() is well-defined, and its ruling angle is exactly $\varphi$
is well-defined, and its ruling angle is exactly $\varphi$![]() . To verify the claim, note that the zero set of $\kappa _{n}(\theta )$
. To verify the claim, note that the zero set of $\kappa _{n}(\theta )$![]() is nowhere dense in $I$
is nowhere dense in $I$![]() , because otherwise there would be an interval where both $\kappa _{n}(\theta )$
, because otherwise there would be an interval where both $\kappa _{n}(\theta )$![]() and $\tau _{g}(\theta )$
and $\tau _{g}(\theta )$![]() vanish, contradicting the assumption of local nonplanarity; thus the ruling angle $\alpha (N(\theta ))$
vanish, contradicting the assumption of local nonplanarity; thus the ruling angle $\alpha (N(\theta ))$![]() is well-defined on a dense subset, where it agrees with $\varphi$
is well-defined on a dense subset, where it agrees with $\varphi$![]() , and so it admits a unique continuous extension to the entire interval.
, and so it admits a unique continuous extension to the entire interval.
Substituting the expressions of $\kappa _{n}(\theta )$![]() and $\tau _{g}(\theta )$
and $\tau _{g}(\theta )$![]() obtained earlier, condition (4.3) becomes
obtained earlier, condition (4.3) becomes
This is a first-order, nonlinear ordinary differential equation in $\theta \colon I \to \mathbb {R}$![]() , which admits a unique local solution for any initial condition $\theta (t_{0}) = q \in [0,\, 2\pi )$
, which admits a unique local solution for any initial condition $\theta (t_{0}) = q \in [0,\, 2\pi )$![]() .
.
It remains to check that the initial value problem is globally solvable, that is, its solution can be extended to the entire interval $I$![]() .
.
Define $F \colon I \times \mathbb {R}$![]() by
by
We are going to show that $F$![]() satisfies the following Lipschitz condition: there exists a constant $c >0$
satisfies the following Lipschitz condition: there exists a constant $c >0$![]() such that, for every $t \in I$
such that, for every $t \in I$![]() and every $x,\,y \in \mathbb {R}$
and every $x,\,y \in \mathbb {R}$![]() ,
,
This way the statement will follow from the classical Picard–Lindelöf theorem; see e.g. [Reference O'Regan17, theorem 3.1].
First of all, note that both $\kappa _{g}\cot (\varphi )$![]() and $\kappa _{n}\cot (\varphi )$
and $\kappa _{n}\cot (\varphi )$![]() are bounded, because they are continuous on the closed interval $I$
are bounded, because they are continuous on the closed interval $I$![]() . Let $l$
. Let $l$![]() and $m$
and $m$![]() be upper bounds for $\lvert \kappa _{g}\cot (\varphi )\rvert$
be upper bounds for $\lvert \kappa _{g}\cot (\varphi )\rvert$![]() and $\lvert \kappa _{n}\cot (\varphi )\rvert$
and $\lvert \kappa _{n}\cot (\varphi )\rvert$![]() , respectively. Computing
, respectively. Computing
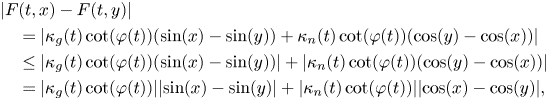
we observe that
and so $F$![]() satisfies the Lipschitz condition with $c = l+m$
satisfies the Lipschitz condition with $c = l+m$![]() , as desired.
, as desired.
Remark 15 It follows from § 3 that $\mathcal {R}(N(\theta ))$![]() has the same ruling angle as $\mathcal {R}(N)$
has the same ruling angle as $\mathcal {R}(N)$![]() if and only if
if and only if
By substituting (4.1) and (4.2), we observe that (4.5) is equivalent to
Compared with (4.4), equation (4.6) offers a shortcut to the construction of the ribbon $\mathcal {R}(V)$![]() defined in corollary 1.4.
defined in corollary 1.4.
Remark 16 The geodesic curvature of $\gamma$![]() with respect to $N(\theta )$
with respect to $N(\theta )$![]() is given by
is given by
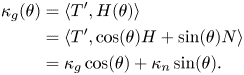
It is easy to see that $\kappa _{g}(\theta )=\kappa _{g}$![]() if and only if $N(\theta ) = N(\pi -2 \bar {\theta })$
if and only if $N(\theta ) = N(\pi -2 \bar {\theta })$![]() , where $\bar {\theta }$
, where $\bar {\theta }$![]() satisfies $\sin (\bar {\theta }) = \kappa _{g}/\kappa$
satisfies $\sin (\bar {\theta }) = \kappa _{g}/\kappa$![]() and $\cos (\bar {\theta }) = \kappa _{n}/\kappa$
and $\cos (\bar {\theta }) = \kappa _{n}/\kappa$![]() . It follows that, if $\kappa >0$
. It follows that, if $\kappa >0$![]() , then there exist pairs of globally isometric flat ribbons along $\gamma$
, then there exist pairs of globally isometric flat ribbons along $\gamma$![]() ; cf. [ Reference Fuchs and Tabachnikov9]. This is in striking contrast to the case of positive Gaussian curvature, where a surface is globally rigid relative to any of its curves [ Reference Ghomi and Spruck10].
; cf. [ Reference Fuchs and Tabachnikov9]. This is in striking contrast to the case of positive Gaussian curvature, where a surface is globally rigid relative to any of its curves [ Reference Ghomi and Spruck10].
5. Bending energy
Let $D$![]() be a flat surface in $\mathbb {R}^{3}$
be a flat surface in $\mathbb {R}^{3}$![]() . The bending energy $\mathcal {E}(D)$
. The bending energy $\mathcal {E}(D)$![]() of $D$
of $D$![]() is defined by
is defined by
where $H$![]() is the mean curvature and ${\rm d}A$
is the mean curvature and ${\rm d}A$![]() the area element of $D$
the area element of $D$![]() .
.
The purpose of this section is to prove theorem 1.9 and corollary 1.11 in the introduction.
theorem If $\mathcal {R}(N)$![]() has width $2w,$
has width $2w,$![]() then its bending energy $\mathcal {E}(\mathcal {R}(N)) =\mathcal {E}(N)$
then its bending energy $\mathcal {E}(\mathcal {R}(N)) =\mathcal {E}(N)$![]() satisfies
satisfies
Proof. Since the integrand is zero whenever $\kappa _{n}(t)=0$![]() , we may assume that $\kappa _{n}$
, we may assume that $\kappa _{n}$![]() is never zero. We need to prove that
is never zero. We need to prove that
where $\mu = -\tau _{g}/\kappa _{n}$![]() .
.
Our first goal is to compute the expressions of the mean curvature and the area element of $\mathcal {R}(N)$![]() in the standard parametrization $\sigma \colon [0,\,L] \times [-w,\,w] \to \mathbb {R}^{3}$
in the standard parametrization $\sigma \colon [0,\,L] \times [-w,\,w] \to \mathbb {R}^{3}$![]() ,
,
This way, we will obtain a formula for the bending energy of a finite-width ribbon $\mathcal {R}(N)$![]() along $\gamma$
along $\gamma$![]() .
.
As the reader may verify, the components of the first and second fundamental forms are
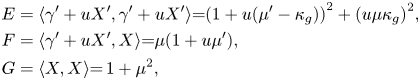
and
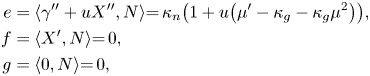
respectively. A computation reveals that the area element is given by
whereas for the mean curvature one obtains
The bending energy may therefore be computed by
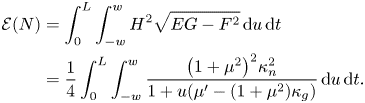
In particular, in the closed subset where $\mu '= (1+\mu ^{2})\kappa _{g}$![]() , the integrand does not depend on $u$
, the integrand does not depend on $u$![]() , and so the inner integral reduces to
, and so the inner integral reduces to
Hence, we may assume that $\mu '(t)\neq (1+\mu (t)^{2})\kappa _{g}(t)$![]() for every $t \in I$
for every $t \in I$![]() . In that case, integration with respect to $u$
. In that case, integration with respect to $u$![]() gives
gives

Our task is now to evaluate the limit of $\mathcal {E}(N)$![]() as $w$
as $w$![]() approaches zero. We first rewrite (5.2) by means of the following notations:
approaches zero. We first rewrite (5.2) by means of the following notations:
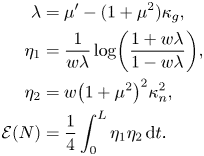
Since $\eta _{1}$![]() converges pointwise to $2$
converges pointwise to $2$![]() as $w \to 0$
as $w \to 0$![]() , it is clear that the integrand $\eta _{1}\eta _{2}$
, it is clear that the integrand $\eta _{1}\eta _{2}$![]() converges pointwise to $0$
converges pointwise to $0$![]() as $w \to 0$
as $w \to 0$![]() . In fact, we will show that the convergence is uniform. Therefore, it will follow from standard analysis [Reference Bartle and Sherbert1, p. 251] that
. In fact, we will show that the convergence is uniform. Therefore, it will follow from standard analysis [Reference Bartle and Sherbert1, p. 251] that
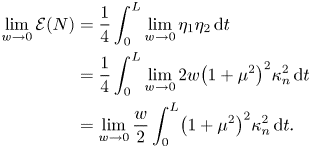
It is evident that $\eta _{2}$![]() is uniformly convergent to $0$
is uniformly convergent to $0$![]() as $w \to 0$
as $w \to 0$![]() . Thus, being $\eta _{1}$
. Thus, being $\eta _{1}$![]() and $\eta _{2}$
and $\eta _{2}$![]() bounded, proving that $\eta _{1}$
bounded, proving that $\eta _{1}$![]() converges uniformly to $2$
converges uniformly to $2$![]() is sufficient to establish uniform convergence of $\eta _{1}\eta _{2}$
is sufficient to establish uniform convergence of $\eta _{1}\eta _{2}$![]() ; see [Reference Bartle and Sherbert1, p. 247].
; see [Reference Bartle and Sherbert1, p. 247].
Let
We need to check that $\max _{t\in I}\lvert \xi (t) \rvert \to 0$![]() as $w \to 0$
as $w \to 0$![]() . To this end, we calculate $\xi '$
. To this end, we calculate $\xi '$![]() and set it equal to $0$
and set it equal to $0$![]() . This leads to
. This leads to
Note that the term multiplying the logarithm only vanishes when $\lambda '$![]() does. Let $J$
does. Let $J$![]() be the zero set of $\lambda '$
be the zero set of $\lambda '$![]() . Then, since $J$
. Then, since $J$![]() is independent of $w$
is independent of $w$![]() , it follows that
, it follows that
On the other hand, in the subinterval $(0,\,L) \setminus J$![]() , we have $\xi '=0$
, we have $\xi '=0$![]() if and only if
if and only if
Together with (5.4), this implies
from which we observe that
Hence,
which is the desired conclusion.
Remark 17 If $\gamma$![]() is locally nonplanar, then, as a function on the set of infinitely narrow flat ribbons along $\gamma$
is locally nonplanar, then, as a function on the set of infinitely narrow flat ribbons along $\gamma$![]() , the bending energy is unbounded. This is because
, the bending energy is unbounded. This is because
when $\tau _{g}(t) \neq 0$![]() , and one can construct flat ribbons along $\gamma$
, and one can construct flat ribbons along $\gamma$![]() of arbitrarily small normal curvature. Indeed, on a subinterval where $\kappa >0$
of arbitrarily small normal curvature. Indeed, on a subinterval where $\kappa >0$![]() , for $x \in \mathbb {R}$
, for $x \in \mathbb {R}$![]() , let $N(x)$
, let $N(x)$![]() be defined by
be defined by
It follows that $\tau _{g}(x) = \tau$![]() and $\kappa _{n}(x) \to 0$
and $\kappa _{n}(x) \to 0$![]() as $x \to \pi /2$
as $x \to \pi /2$![]() .
.
On the other hand, under the same assumption of local nonplanarity, the bending energy has a positive lower bound. Thus, one may search for the ruling angle and initial condition in $\gamma '(0)^{\perp }$![]() that give the least bending energy. This is a very interesting problem, which the author hopes will be the subject of future study.
that give the least bending energy. This is a very interesting problem, which the author hopes will be the subject of future study.
Corollary If $\mathcal {R}(N)$![]() and $\mathcal {R}(V)$
and $\mathcal {R}(V)$![]() are flat ribbons along $\gamma$
are flat ribbons along $\gamma$![]() with the same ruling angle, then, in the limit of infinitely small widths, their bending energies $\mathcal {E}(N)$
with the same ruling angle, then, in the limit of infinitely small widths, their bending energies $\mathcal {E}(N)$![]() and $\mathcal {E}(V)$
and $\mathcal {E}(V)$![]() satisfy
satisfy
where $\kappa _{g}$![]() is the geodesic curvature of $\gamma$
is the geodesic curvature of $\gamma$![]() with respect to $N$
with respect to $N$![]() . In particular, if the normal curvature $\kappa _{n}$
. In particular, if the normal curvature $\kappa _{n}$![]() of $\gamma$
of $\gamma$![]() with respect to $N$
with respect to $N$![]() is always nonzero, then
is always nonzero, then
where $\rho = \kappa _{g}/\kappa _{n}$![]() and $\phi$
and $\phi$![]() is the angle between $N$
is the angle between $N$![]() and $\gamma ''$
and $\gamma ''$![]() .
.
Proof. Let $\mathcal {R}(N)$![]() and $\mathcal {R}(V=N(\theta ))$
and $\mathcal {R}(V=N(\theta ))$![]() be flat ribbons along $\gamma$
be flat ribbons along $\gamma$![]() with the same ruling angle. By theorem 1.9, the bending energy of $\mathcal {R}(V)$
with the same ruling angle. By theorem 1.9, the bending energy of $\mathcal {R}(V)$![]() satisfies
satisfies

Since $\kappa _{n}(\theta )^{2} \leq \kappa ^{2} = \kappa _{n}^{2} + \kappa _{g}^{2}$![]() , assuming that $w$
, assuming that $w$![]() is infinitely small, we obtain
is infinitely small, we obtain
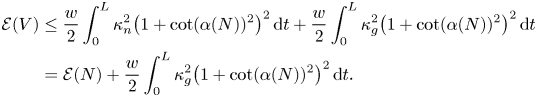
Now, suppose that $\kappa _{n}(t) \neq 0$![]() for all $t \in I$
for all $t \in I$![]() , and let $\rho = \kappa _{g}/\kappa _{n}$
, and let $\rho = \kappa _{g}/\kappa _{n}$![]() . Then
. Then
Noting that the integrand in the equation above is a product of nonnegative functions, by invoking the first mean value theorem for integrals [Reference Bartle and Sherbert1, p. 301], we deduce that there exists $s \in I$![]() such that
such that
Hence
and the assertion of the corollary follows.
6. Special cases
In this section we study the set of flat ribbons along a locally nonplanar curve $\gamma$![]() under two natural choices of ruling angle $\alpha$
under two natural choices of ruling angle $\alpha$![]() :
:
(A) $\alpha$
 is constant and equal to $\pi /2$
is constant and equal to $\pi /2$ .
.(B) Assuming $\kappa >0$
 , $\alpha$
, $\alpha$ coincides with the ruling angle of the rectifying developable of $\gamma$
coincides with the ruling angle of the rectifying developable of $\gamma$ .
.
Case A. Note from (3.2) that $\alpha (N)=\pi /2$![]() if and only if $\tau _{g}=0$
if and only if $\tau _{g}=0$![]() . Hence, between any two consecutive zeros of $\kappa _{n}$
. Hence, between any two consecutive zeros of $\kappa _{n}$![]() , equation (4.6) reduces to $\theta '=0$
, equation (4.6) reduces to $\theta '=0$![]() . Assuming $\kappa _{n}(t) \neq 0$
. Assuming $\kappa _{n}(t) \neq 0$![]() everywhere, it follows that the initial value problem (defined by $\theta (0)=q$
everywhere, it follows that the initial value problem (defined by $\theta (0)=q$![]() ) has constant solution $\theta =q$
) has constant solution $\theta =q$![]() .
.
Applying (5.5) and (4.1), we then observe that the bending energy of $\mathcal {R}(N(q))$![]() , under the hypothesis of infinitely small width, is given by
, under the hypothesis of infinitely small width, is given by
In order to analyse the dependence of the bending energy on the initial condition, we calculate ${\rm d}\mathcal {E}(N(q))/{\rm d} q$![]() and set it equal to zero. This leads to
and set it equal to zero. This leads to
where
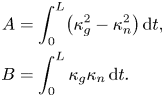
First, suppose that $A=B=0$![]() . Then the energy is independent of $q$
. Then the energy is independent of $q$![]() , and
, and
Else, if $B=0$![]() and $A \neq 0$
and $A \neq 0$![]() , then ${\rm d}\mathcal {E}(N(q))/{\rm d} q\!=0$
, then ${\rm d}\mathcal {E}(N(q))/{\rm d} q\!=0$![]() if and only if $\sin (q)\!=\!0$
if and only if $\sin (q)\!=\!0$![]() or $\cos (q)\!=\!0$
or $\cos (q)\!=\!0$![]() , implying that the extreme values of $\mathcal {E}(N(q))$
, implying that the extreme values of $\mathcal {E}(N(q))$![]() are
are
Next, suppose that $B \neq 0$![]() . Noting that ${\rm d}\mathcal {E}(N(q))/{\rm d}q\neq 0$
. Noting that ${\rm d}\mathcal {E}(N(q))/{\rm d}q\neq 0$![]() if $B\neq 0$
if $B\neq 0$![]() and $\sin (q)=0$
and $\sin (q)=0$![]() , we may assume that $B\neq 0$
, we may assume that $B\neq 0$![]() and $\sin (q)\neq 0$
and $\sin (q)\neq 0$![]() . Consequently, ${\rm d}\mathcal {E}(N(q))/{\rm d} q$
. Consequently, ${\rm d}\mathcal {E}(N(q))/{\rm d} q$![]() vanishes if and only if
vanishes if and only if
which have solutions
Substitution of (6.3) into (6.1), alongside an easy, if tedious, calculation, demonstrates that
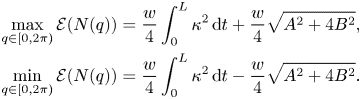
Case B. It is clear that, if $N= T'/\lVert T'\rVert$![]() , then $\kappa _{g}=0$
, then $\kappa _{g}=0$![]() , $\kappa _{n}=\kappa$
, $\kappa _{n}=\kappa$![]() , and $\tau _{g}=\tau$
, and $\tau _{g}=\tau$![]() . Hence in this case equation (4.6) simplifies to the separable equation
. Hence in this case equation (4.6) simplifies to the separable equation
Letting $\psi (t)= \int _{0}^{t} \tau (z) \, {\rm d}z$![]() , the solution is
, the solution is
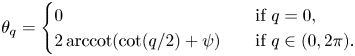
As for the bending energy, equation (5.5) now yields
Substituting (6.4), we obtain
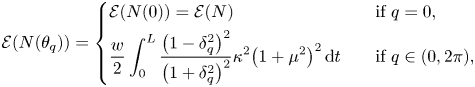
where $\delta _{q}=\cot (q/2)+ \psi$![]() .
.
7. The helix
We conclude the paper by applying the results of the previous section to a specific curve, namely a circular helix of radius $a$![]() and pitch $2\pi b$
and pitch $2\pi b$![]() :
:
The curvature and torsion are $a/(a^{2}+b^{2})$![]() and $b/(a^{2}+b^{2})$
and $b/(a^{2}+b^{2})$![]() , respectively; they coincide with the normal curvature and geodesic torsion of $\gamma$
, respectively; they coincide with the normal curvature and geodesic torsion of $\gamma$![]() with respect to $\gamma ''/\lVert \gamma ''\rVert = N$
with respect to $\gamma ''/\lVert \gamma ''\rVert = N$![]() .
.
We first examine the case $\alpha =\pi /2$![]() . Setting $\varphi =\pi /2$
. Setting $\varphi =\pi /2$![]() and $\tau _{g} = b/(a^{2}+b^{2})$
and $\tau _{g} = b/(a^{2}+b^{2})$![]() , equation (4.4) becomes
, equation (4.4) becomes
and so
is a solution, i.e. $\alpha (N(\theta )) = \pi /2$![]() . It follows that the normal and geodesic curvatures with respect to $N(\theta )$
. It follows that the normal and geodesic curvatures with respect to $N(\theta )$![]() are
are
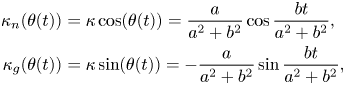
whereas $\tau _{g}(\theta )=0$![]() , as desired. Applying formula (6.1) to $N(\theta )$
, as desired. Applying formula (6.1) to $N(\theta )$![]() , we obtain
, we obtain
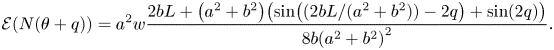
Letting $r =bL/(a^{2}+b^{2})$![]() and normalizing by $\mathcal {E}(N(\theta ))$
and normalizing by $\mathcal {E}(N(\theta ))$![]() , we finally get
, we finally get
Figure 2 displays the graph of the function $q\mapsto \mathcal {E}(N(\theta +q))/\mathcal {E}(N(\theta ))$![]() for different values of the parameter $r$
for different values of the parameter $r$![]() .
.
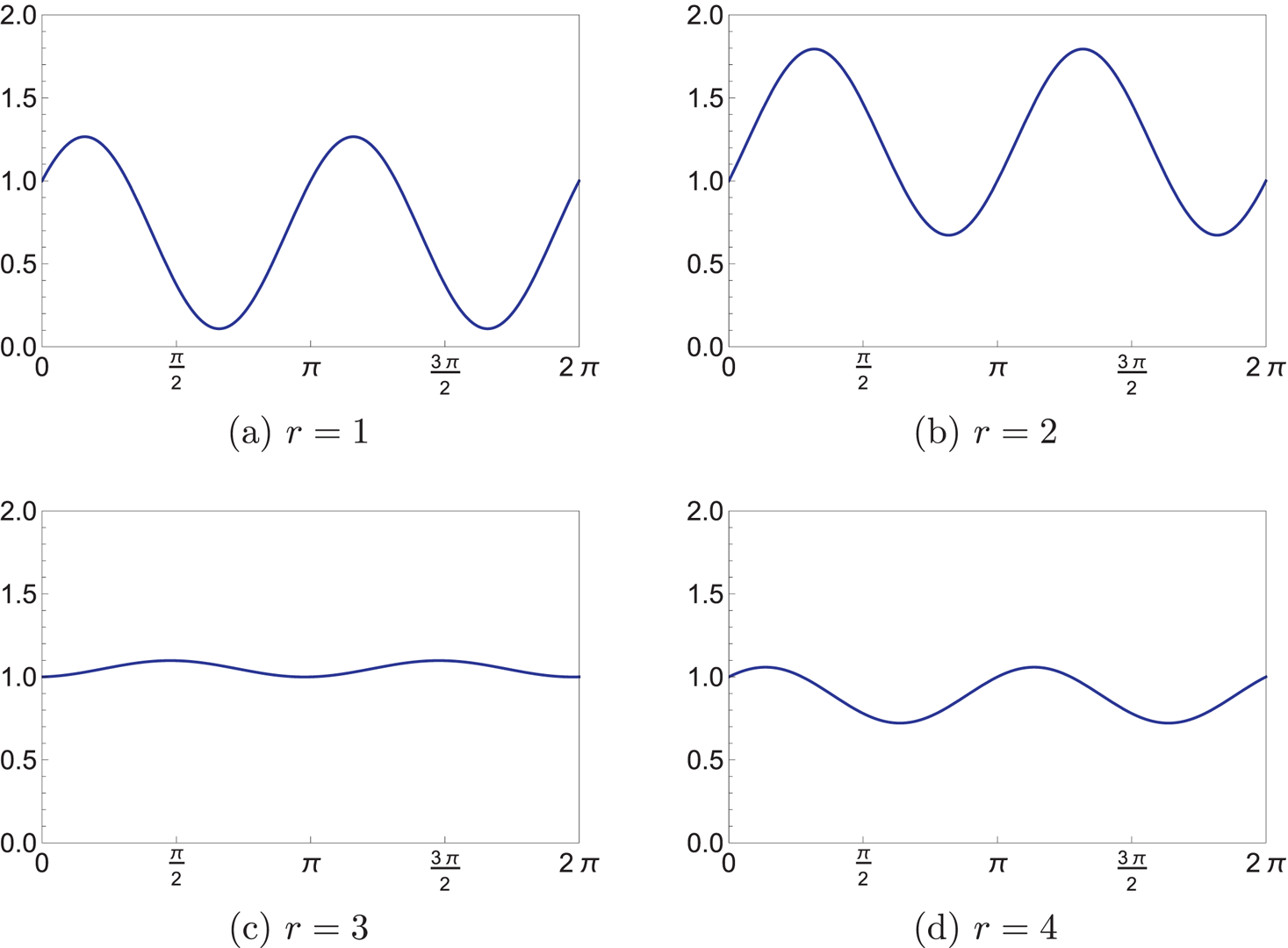
FIGURE 2. Plots of the normalized bending energy (7.1) as a function of $q$![]() for several values of $r$
for several values of $r$![]() . (a) $r=1$
. (a) $r=1$![]() , (b) $r=2$
, (b) $r=2$![]() , (c) $r=3$
, (c) $r=3$![]() , (d) $r=4$
, (d) $r=4$![]() .
.
We then turn our attention to the case in which $\alpha$![]() coincides with the ruling angle of the rectifying developable. The bending energy is now given by (6.5). For $q=0$
coincides with the ruling angle of the rectifying developable. The bending energy is now given by (6.5). For $q=0$![]() it reads
it reads
On the other hand, if $q\neq 0$![]() , then $\delta _{q}=\cot (q/2)+\psi$
, then $\delta _{q}=\cot (q/2)+\psi$![]() , where $\psi (t)= b t/(a^{2}+b^{2})$
, where $\psi (t)= b t/(a^{2}+b^{2})$![]() . A computation reveals that
. A computation reveals that
from which one easily obtains $\mathcal {E}(N(\theta _{q}))$![]() . In particular, it follows that
. In particular, it follows that
As in the previous case, the graph of function $q\mapsto \mathcal {E}(N(\theta _{q})/\mathcal {E}(N)$![]() is plotted for different choices of $r$
is plotted for different choices of $r$![]() in figure 3.
in figure 3.
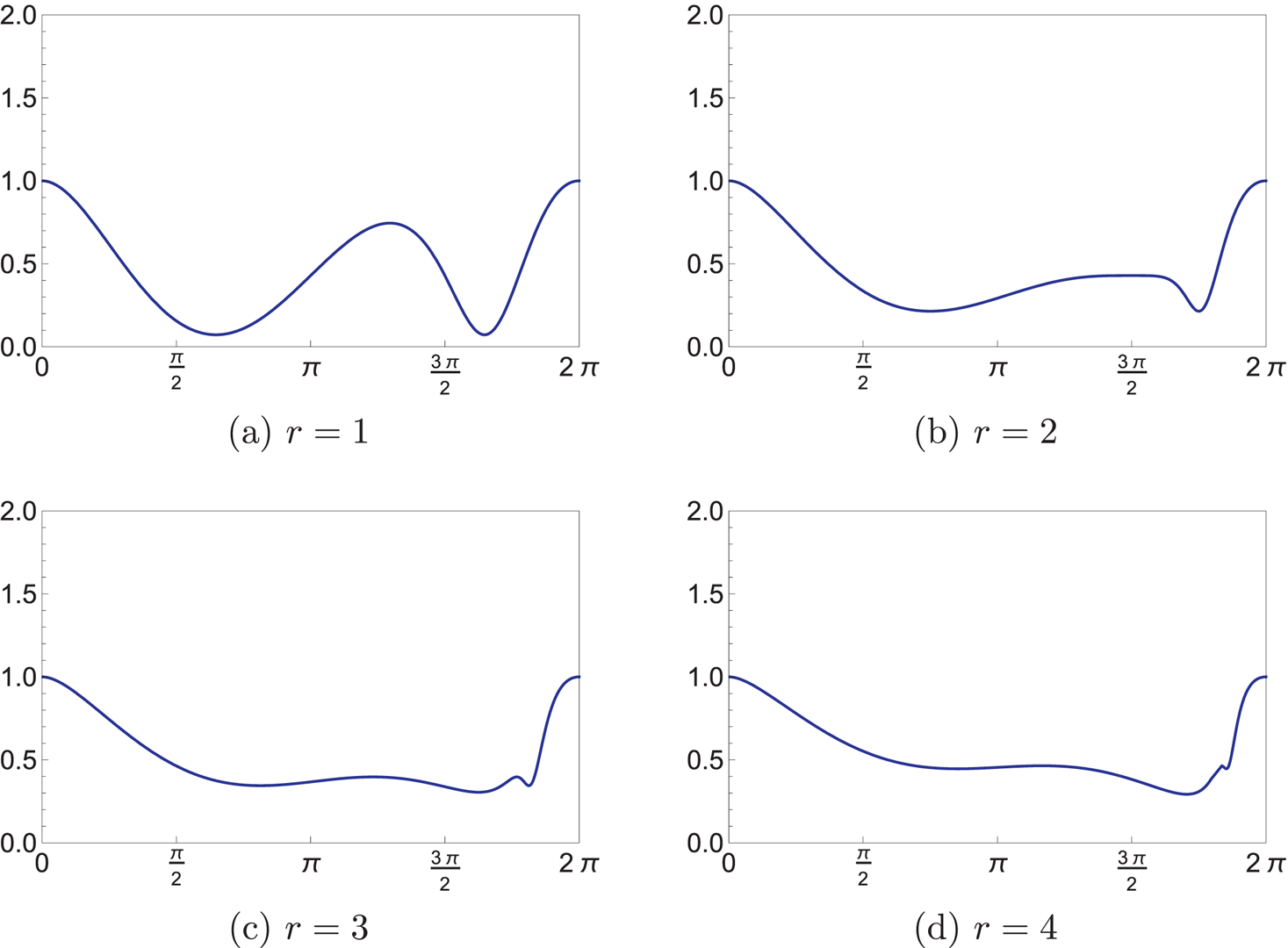
FIGURE 3. Plots of the normalized bending energy (7.2) as a function of $q$![]() for several values of $r$
for several values of $r$![]() . (a) $r=1$
. (a) $r=1$![]() , (b) $r=2$
, (b) $r=2$![]() , (c) $r=3$
, (c) $r=3$![]() , (d) $r=4$
, (d) $r=4$![]() .
.
It is worth pointing out that, in both cases treated, the bending energy becomes less and less dependent on the initial condition as $r$![]() increases. More precisely, one can check that both ratios (7.1) and (7.2) tend to $1$
increases. More precisely, one can check that both ratios (7.1) and (7.2) tend to $1$![]() as $r \to \infty$
as $r \to \infty$![]() . It seems reasonable to expect that the same conclusion holds for any choice of ruling angle. Proving this is outside the scope of the present study.
. It seems reasonable to expect that the same conclusion holds for any choice of ruling angle. Proving this is outside the scope of the present study.
Acknowledgements
The author thanks David Brander, Christian Müller and an anonymous referee for many helpful comments and suggestions.
Financial support
This work was supported by Austrian Science Fund (FWF) project F 77 (SFB ‘Advanced Computational Design’).