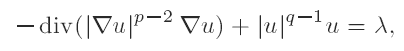In this paper, we study the non-existence of solutions for the following (model) problem in a bounded open subset Ω of RN:with Dirichlet boundary conditions, where p > 1, q > 1 and μ is a bounded Radon measure. We prove that if λ is a measure which is concentrated on a set of zero r capacity (p < r ≤ N), and if q > r (p − 1)/(r − p), then there is no solution to the above problem, in the sense that if one approximates the measure λ with a sequence of regular functions fn, and if un is the sequence of solutions of the corresponding problems, then un converges to zero.

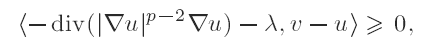We also study the non-existence of solutions for the bilateral obstacle problem with datum a measure λ concentrated on a set of zero p capacity,with u in for every υ in K, finding again that the only solution obtained by approximation is u = 0.