Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T19:30:55.589Z Has data issue: false hasContentIssue false
  • English
  • Français

Nodal solutions for the fractional Yamabe problem on Heisenberg groups

Part of: Partial differential equations Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  26 January 2019

Alexandru Kristály
Alexandru Kristály*
Affiliation:
Department of Economics, Babeş-Bolyai University, Cluj-Napoca400591, Romania and Institute of Applied Mathematics, Óbuda University, Budapest 1034, Hungary ([email protected]; [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that the fractional Yamabe equation 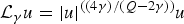${\rm {\cal L}}_\gamma u = \vert u \vert ^{((4\gamma )/(Q-2\gamma ))}u$ on the Heisenberg group ℍn has [n + 1/2] sequences of nodal (sign-changing) weak solutions whose elements have mutually different nodal properties, where 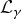${\rm {\cal L}}_\gamma $ denotes the CR fractional sub-Laplacian operator on ℍn, Q = 2n + 2 is the homogeneous dimension of ℍn, and 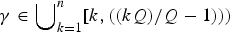$\gamma \in \bigcup\nolimits_{k = 1}^n [k,((kQ)/Q-1)))$. Our argument is variational, based on a Ding-type conformal pulling-back transformation of the original problem into a problem on the CR sphere S2n + 1 combined with a suitable Hebey-Vaugon-type compactness result and group-theoretical constructions for special subgroups of the unitary group U(n + 1).

Keywords

CR fractional sub-Laplaciannodal solutionHeisenberg group

MSC classification

Primary: 35R03: Partial differential equations on Heisenberg groups, Lie groups, Carnot groups, etc.
Secondary: 35B38: Critical points
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 771 - 788
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Dedicated to Professor Patrizia Pucci on the occasion of her 65th birthday.

References

1Aubin, T.. Nonlinear analysis on manifolds, Monge-Ampère equations (New York: Springer-Verlag, 1982).CrossRefGoogle Scholar
2Balogh, Z. M. and Kristály, A.. Lions-type compactness and Rubik actions on the Heisenberg group. Calc. Var. Partial Differ. Equ. 48 (2013), 89–109.CrossRefGoogle Scholar
3Bartsch, T. and Willem, M.. Infinitely many nonradial solutions of a Euclidean scalar field equation. J. Funct. Anal. 117 (1993), 447–460.CrossRefGoogle Scholar
4Bartsch, T., Schneider, M. and Weth, T.. Multiple solutions of a critical polyharmonic equation. J. Reine Angew. Math. 571 (2004), 131–143.Google Scholar
5Branson, T. P., Fontana, L. and Morpurgo, C.. Moser-Trudinger and Beckner-Onofri's inequalities on the CR sphere. Ann. of Math. 177 (2013), 1–52.CrossRefGoogle Scholar
6Cabré, X. and Sire, Y.. Nonlinear equations for fractional Laplacians I: regularity, maximum principles, and Hamiltonian estimates. Ann. Inst. H. Poincaré Anal. Non Linéaire 31 (2014), 23–53.CrossRefGoogle Scholar
7Caffarelli, L.. Nonlocal equations drifts and games. Nonlinear Partial Differ. Equ., Abel Symposia 7 (2012), 37–52.CrossRefGoogle Scholar
8Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Comm. Partial Differ. Equ. 32 (2007), 1245–1260.CrossRefGoogle Scholar
9Caffarelli, L., Salsa, S. and Silvestre, L.. Regularity estimates for the solution and the free boundary of the obstacle problem for the fractional Laplacian. Invent. Math. 171 (2008), 425–461.CrossRefGoogle Scholar
10Di Nezza, E., Palatucci, G. and Valdinoci, E.. Hitchhiker's guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573.CrossRefGoogle Scholar
11Ding, W. Y.. On a conformally invariant elliptic equation. Comm. Math. Phys. 107 (1986), 331–335.Google Scholar
12Folland, G. B.. A fundamental solution for a subelliptic operator. Bull. Amer. Math. Soc. 79 (1973), 373–376.CrossRefGoogle Scholar
13Folland, G. B.. Spherical harmonics expansion of the Poisson-Szegő kernel for the ball. Proc. Amer. Math. Soc. 47 (1975), 401–408.Google Scholar
14Frank, R. L. and Lieb, E. H.. Sharp constants in several inequalities on the Heisenberg group. Ann. Math. 176 (2012), 349–381.Google Scholar
15Frank, R., del Mar González, M., Monticelli, D. D. and Tan, J.. An extension problem for the CR fractional Laplacian. Adv. Math. 270 (2015), 97–137.CrossRefGoogle Scholar
16Garofalo, N. and Vassilev, D.. Symmetry properties of positive entire solutions of Yamabe-type equations on groups of Heisenberg type. Duke Math J. 106 (2001), 411–448.CrossRefGoogle Scholar
17Hebey, E. and Vaugon, M.. Sobolev spaces in the presence of symmetries. J. Math. Pures Appl. 76 (1997), 859–881.CrossRefGoogle Scholar
18Jerison, D. and Lee, J. M.. The Yamabe problem on CR manifolds. J. Differ. Geom. 25 (1987), 167–197.CrossRefGoogle Scholar
19Jerison, D. and Lee, J. M.. Extremals for the Sobolev inequality on the Heisenberg group and the CR Yamabe problem. J. Amer. Math. Soc. 1 (1988), 1–13.CrossRefGoogle Scholar
20Maalaoui, A. and Martino, V.. Changing-sign solutions for the CR-Yamabe equation. Differ. Integral Equ. 25 (2012), 601–609.Google Scholar
21Maalaoui, A., Martino, V. and Tralli, G.. Complex group actions on the sphere and sign changing solutions for the CR-Yamabe equation. J. Math. Anal. Appl. 431 (2015), 126–135.CrossRefGoogle Scholar
22Palais, R. S.. The principle of symmetric criticality. Comm. Math. Phys. 69 (1979), 19–30.CrossRefGoogle Scholar
23Vilenkin, N. J. and Klimyk, A. U.. Representation of Lie groups and special functions. Class I representations, special functions, and integral transforms vol. 2, Translated from the Russian by V. A. Groza and A. A. Groza. Mathematics and its applications (Soviet Series), 74 (Dordrecht: Kluwer Academic Publishers Group, 1993).CrossRefGoogle Scholar