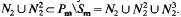Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T01:55:17.784Z Has data issue: false hasContentIssue false
  • English
  • Français

A nilpotent-generated semigroup associated with a semigroup of full transformations

Published online by Cambridge University Press:  14 November 2011

John M. Howie  and
M. Paula O. Marques-Smith
John M. Howie
Affiliation:
Mathematical Institute, University of St Andrews, North Haugh, St Andrews KY16 9SS, Scotland, U.K.
M. Paula O. Marques-Smith
Affiliation:
Area de Matematica, Universidade do Minho, 4700 Braga, Portugal
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let X be a set with infinite regular cardinality m and let ℱ(X) be the semigroup of all self-maps of X. The semigroup Qm of ‘balanced’ elements of ℱ(X) plays an important role in the study by Howie [3,5,6] of idempotent-generated subsemigroups of ℱ(X), as does the subset Sm of ‘stable’ elements, which is a subsemigroup of Qm if and only if m is a regular cardinal. The principal factor Pm of Qm, corresponding to the maximum ℱ-class Jm, contains Sm and has been shown in [7] to have a number of interesting properties.

Let N2 be the set of all nilpotent elements of index 2 in Pm. Then the subsemigroup (N2) of Pm generated by N2 consists exactly of the elements in Pm/Sm. Moreover Pm/Sm has 2-nilpotent-depth 3, in the sense that

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 108 , Issue 1-2 , 1988 , pp. 181 - 187
Copyright
Copyright © Royal Society of Edinburgh 1988

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Clifford, A. H. and Preston, G. B.. The algebraic theory of semigroups, vols. 1 and 2 (Providence, R.I.: American Mathematical Society, 1961 and 1967).Google Scholar
2Halmos, P. R.. Naive set theory (New York: Van Nostrand, 1960).Google Scholar
3Howie, J. M.. The semigroup generated by the idempotents of a full transformation semigroup. J. London Math. Soc. 41 (1966), 707–716.Google Scholar
4Howie, J. M.. An introduction to semigroup theory (London: Academic Press, 1976).Google Scholar
5Howie, J. M.. Some subsemigroups of infinite full transformation semigroups. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 159–167.Google Scholar
6Howie, J. M.. A class of bisimple, idempotent-generated congruence-free semigroups. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 169–184.Google Scholar
7Paula, M.Marques, O.. A congruence-free semigroup associated with an infinite cardinal number. Proc. Roy. Soc. Edinburgh Sect. A 93 (1983), 245–257.Google Scholar
8Paula, M.Marques, O.. Infinite Transformation Semigroups (Ph.D. Thesis, University of St. Andrews, 1983.)Google Scholar
9Preston, G. B.. A characterization of inaccessible cardinals. Proc. Glasgow Math. Assoc. S (1962), 152–157.CrossRefGoogle Scholar