Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T13:33:30.308Z Has data issue: false hasContentIssue false
  • English
  • Français

New variable martingale Hardy spaces

Part of: Stochastic processes

Published online by Cambridge University Press:  23 April 2021

Yong Jiao ,
Dan Zeng  and
Dejian Zhou
Yong Jiao
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha410075, People's Republic of China ([email protected]; [email protected] and [email protected])
Dan Zeng
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha410075, People's Republic of China ([email protected]; [email protected] and [email protected])
Dejian Zhou
Affiliation:
School of Mathematics and Statistics, Central South University, Changsha410075, People's Republic of China ([email protected]; [email protected] and [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

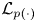We investigate various variable martingale Hardy spaces corresponding to variable Lebesgue spaces $\mathcal {L}_{p(\cdot )}$ defined by rearrangement functions. In particular, we show that the dual of martingale variable Hardy space 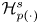$\mathcal {H}_{p(\cdot )}^{s}$ with 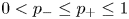$0<p_{-}\leq p_{+}\leq 1$ can be described as a BMO-type space and establish martingale inequalities among these martingale Hardy spaces. Furthermore, we give an application of martingale inequalities in stochastic integral with Brownian motion.

Keywords

variable exponentrearrangement functionmartingale inequalitiesatomic decompositionduality

MSC classification

Primary: 60G46: Martingales and classical analysis
Secondary: 60G42: Martingales with discrete parameter
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 152 , Issue 2 , April 2022 , pp. 450 - 478
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aoyama, H.. Lebesgue spaces with variable exponent on a probability space. Hiroshima Math. J. 39 (2009), 207–216. MR 2543650.CrossRefGoogle Scholar
Bennett, C. and Sharpley, R.. Interpolation of operators, Pure and Applied Mathematics, vol. 129 (Boston, MA: Academic Press, Inc., 1988) MR 928802.Google Scholar
Cruz-Uribe, D. and Fiorenza, A.. Variable Lebesgue spaces, Applied and Numerical Harmonic Analysis (Heidelberg: Birkhäuser/Springer, 2013) Foundations and harmonic analysis. MR 3026953.CrossRefGoogle Scholar
Cruz-Uribe, D. and Wang, L.. Variable Hardy spaces. Indiana Univ. Math. J. 63 (2014), 447–493. MR 3233216.Google Scholar
Diening, L.. Maximal function on generalized Lebesgue spaces $L^{p}(\cdot )$. Math. Inequal. Appl. 7 (2004), 245–253. MR 2057643.Google Scholar
Diening, L.. Maximal function on Musielak-Orlicz spaces and generalized Lebesgue spaces. Bull. Sci. Math. 129 (2005), 657–700. MR 2166733.CrossRefGoogle Scholar
Diening, L. and Samko, S.. Hardy inequality in variable exponent Lebesgue spaces. Fract. Calc. Appl. Anal. 10 (2007), 1–18. MR 2348863.Google Scholar
Diening, L., Harjulehto, P., Hästö, P. and Růžička, M.. Lebesgue and Sobolev spaces with variable exponents. Lecture Notes in Mathematics, vol. 2017 (Heidelberg: Springer, 2011).CrossRefGoogle Scholar
Ephremidze, L., Kokilashvili, V. and Samko, S.. Fractional, maximal and singular operators in variable exponent Lorentz spaces. Fract. Calc. Appl. Anal. 11 (2008), 407–420. MR 2459733.Google Scholar
Fan, X. and Zhao, D.. On the spaces $L^{p}(x)(\Omega )$ and $W^{m},p(x)(\Omega )$. J. Math. Anal. Appl. 263 (2001), 424–446. MR 1866056.CrossRefGoogle Scholar
Grafakos, L.. Classical Fourier analysis, 2nd edn, vol. 249, Graduate Texts in Mathematics (New York: Springer, 2008) MR 2445437.Google Scholar
Hao, Z. and Jiao, Y.. Fractional integral on martingale Hardy spaces with variable exponents. Fract. Calc. Appl. Anal. 18 (2015), 1128–1145. MR 3417085.Google Scholar
Jiao, Y., Zhou, D., Hao, Z. and Chen, W.. Martingale Hardy spaces with variable exponents. Banach J. Math. Anal. 10 (2016), 750–770. MR 3548624.CrossRefGoogle Scholar
Jiao, Y., Zhou, D., Weisz, F. and Hao, Z.. Corrigendum: fractional integral on martingale Hardy spaces with variable exponents. Fract. Calc. Appl. Anal. 20 (2017), 1051–1052. MR 3684883.CrossRefGoogle Scholar
Jiao, Y., Zuo, Y., Zhou, D. and Wu, L.. Variable Hardy-Lorentz spaces $H^{p(\cdot ),q}(\mathbb {R}^{n})$. Math. Nachr. 292 (2019), 309–349.CrossRefGoogle Scholar
Jiao, Y., Weisz, F., Wu, L. and Zhou, D.. Variable martingale Hardy spaces and their applications in Fourier analysis. Dissertationes Math. 550 (2020), 67 pp.CrossRefGoogle Scholar
Jiao, Y., Zhao, T. and Zhou, D.. Variable martingale Hardy-Morrey spaces. J. Math. Anal. Appl. 484 (2020), 123722, 26. MR 4038182.CrossRefGoogle Scholar
Kokilashvili, V. and Samko, S.. Singular integrals and potentials in some Banach function spaces with variable exponent. J. Funct. Spaces Appl. 1 (2003), 45–59. MR 2011500.CrossRefGoogle Scholar
Kokilashvili, V. and Samko, S.. Maximal and fractional operators in weighted $L^{p}(x)$ spaces. Rev. Mat. Iberoamericana 20 (2004), 493–515. MR 2073129.CrossRefGoogle Scholar
Kováčik, O. and Rákosník, J.. On spaces $L^{p}(x)$ and $W^{k},p(x)$. Czechoslovak Math. J. 41 (1991) 592–618. MR 1134951.CrossRefGoogle Scholar
Liu, J., Yang, D. and Yuan, W.. Anisotropic Hardy-Lorentz spaces and their applications. Sci. China Math. 59 (2016), 1669–1720. MR 3536030.CrossRefGoogle Scholar
Liu, J., Weisz, F., Yang, D. and Yuan, W.. Littlewood-Paley and finite atomic characterizations of anisotropic variable Hardy-Lorentz spaces and their applications. J. Fourier Anal. Appl. 25 (2019), 874–922. MR 3953490.CrossRefGoogle Scholar
Long, R.. Martingale spaces and inequalities (Beijing: Peking University Press, Friedr. Vieweg & Sohn, Braunschweig, 1993) MR 1224450.CrossRefGoogle Scholar
Mao, X.. Stochastic differential equations and applications, 2nd edn (Chichester: Horwood Publishing Limited, 2008) MR 2380366.CrossRefGoogle Scholar
Nakai, E. and Sawano, Y.. Hardy spaces with variable exponents and generalized Campanato spaces. J. Funct. Anal. 262 (2012), 3665–3748. MR 2899976.CrossRefGoogle Scholar
Nakai, E. and Sadasue, G.. Maximal function on generalized martingale Lebesgue spaces with variable exponent. Statist. Probab. Lett. 83 (2013), 2168–2171. MR 3093797.CrossRefGoogle Scholar
Orlicz, W.. Über konjugierte exponentenfolgen. Stidia Math. 3 (1931), 200–211.CrossRefGoogle Scholar
Weisz, F.. Martingale Hardy spaces, their applications in Fourier analysis. Lecture Notes in Mathematics, vol. 1568 (Berlin: Springer-Verlag, 1994). MR 1320508.CrossRefGoogle Scholar
Wu, L., Hao, Z. and Jiao, Y.. John-nirenberg inequalities with variable exponents on probability spaces. Tokyo J. Math. 38 (2015), 352–367.Google Scholar
Wu, L., Zhou, D., Zhuo, C. and Jiao, Y.. Riesz transform characterizations of variable Hardy-Lorentz spaces. Rev. Mat. Complut. 31 (2018), 747–780. MR 3847083.CrossRefGoogle Scholar
Yan, X., Yang, D., Yuan, W. and Zhuo, C.. Variable weak Hardy spaces and their applications. J. Funct. Anal. 271 (2016), 2822–2887. MR 3548281.CrossRefGoogle Scholar
Zhikov, V.. Averaging of functionals of the calculus of variations and elasticity theory, Izv. Akad. Nauk SSSR Ser. Mat. 50 (1986), 675–710. 877.Google Scholar
Zhikov, V.. The Lavrentiev effect and averaging of nonlinear variational problems. Differentsial'nye Uravneniya. 27 (1991), 42–50. 180.Google Scholar
Zhikov, V.. On Lavrentiev's phenomenon. Russian J. Math. Phys. 3 (1995), 249–269.Google Scholar