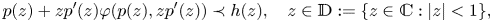1. Introduction
Given $r>0,$![]() let $\mathbb {D}_r:=\{z\in \mathbb {C}: |z|< r\}$
let $\mathbb {D}_r:=\{z\in \mathbb {C}: |z|< r\}$![]() . Let $\mathbb {D}:=\mathbb {D}_1$
. Let $\mathbb {D}:=\mathbb {D}_1$![]() and $\mathbb {T}:=\{z\in \mathbb {C}:|z|=1\}.$
and $\mathbb {T}:=\{z\in \mathbb {C}:|z|=1\}.$![]() For $D$
For $D$![]() being a domain in $\mathbb {C}$
being a domain in $\mathbb {C}$![]() let $\mathcal {H}(D)$
let $\mathcal {H}(D)$![]() be the family of all analytic functions $f: D\rightarrow \mathbb {C}$
be the family of all analytic functions $f: D\rightarrow \mathbb {C}$![]() and $\mathcal {H}:=\mathcal {H}(\mathbb {D}).$
and $\mathcal {H}:=\mathcal {H}(\mathbb {D}).$![]() Let $\mathcal {A}$
Let $\mathcal {A}$![]() be the subclass of $\mathcal {H}$
be the subclass of $\mathcal {H}$![]() of $f$
of $f$![]() normalized by $f(0)=0=f'(0)-1,$
normalized by $f(0)=0=f'(0)-1,$![]() and $\mathcal {S}$
and $\mathcal {S}$![]() be the subclass of $\mathcal {A}$
be the subclass of $\mathcal {A}$![]() of univalent functions.
of univalent functions.
For $r\in (0,\,1)$![]() and $f\in \mathcal {H},$
and $f\in \mathcal {H},$![]() let $f_r(z):=f(rz)$
let $f_r(z):=f(rz)$![]() , $z\in \overline {\mathbb {D}}:=\{z\in \mathbb {C}:|z|\le 1\}.$
, $z\in \overline {\mathbb {D}}:=\{z\in \mathbb {C}:|z|\le 1\}.$![]() Clearly, each $f_r$
Clearly, each $f_r$![]() is analytic in $\overline {\mathbb {D}}.$
is analytic in $\overline {\mathbb {D}}.$![]()
A function $f\in \mathcal {H}$![]() is said to be subordinate to a function $g\in \mathcal {H}$
is said to be subordinate to a function $g\in \mathcal {H}$![]() if there exists $\omega \in \mathcal {H}$
if there exists $\omega \in \mathcal {H}$![]() such that $\omega (0)=0,$
such that $\omega (0)=0,$![]() $\omega (\mathbb {D})\subset \mathbb {D}$
$\omega (\mathbb {D})\subset \mathbb {D}$![]() and $f=g\circ \omega$
and $f=g\circ \omega$![]() in $\mathbb {D}.$
in $\mathbb {D}.$![]() We write then $f\prec g.$
We write then $f\prec g.$![]() If $g$
If $g$![]() is univalent, then (e.g., [Reference Goodman3, Vol. I, p. 85])
is univalent, then (e.g., [Reference Goodman3, Vol. I, p. 85])
Given $\psi : \mathbb {C}^2\rightarrow \mathbb {C},$![]() let $\mathcal {H}[\psi ]$
let $\mathcal {H}[\psi ]$![]() be the subset of $\mathcal {H}$
be the subset of $\mathcal {H}$![]() of all $p$
of all $p$![]() such that a function $\mathbb {D} \ni z\mapsto \psi (p(z),\,zp'(z))$
such that a function $\mathbb {D} \ni z\mapsto \psi (p(z),\,zp'(z))$![]() is well-defined and analytic.
is well-defined and analytic.
Let $\psi : \mathbb {C}^2\rightarrow \mathbb {C}$![]() and $h\in \mathcal {H}$
and $h\in \mathcal {H}$![]() be univalent. We say that a function $p\in \mathcal {H}[\psi ]$
be univalent. We say that a function $p\in \mathcal {H}[\psi ]$![]() satisfies the first-order differential subordination and is called its solution if
satisfies the first-order differential subordination and is called its solution if
If $q\in \mathcal {H}$![]() is a univalent function such that $p\prec q$
is a univalent function such that $p\prec q$![]() for all $p$
for all $p$![]() satisfying (1.2), then $q$
satisfying (1.2), then $q$![]() is called a dominant of (1.2). A dominant $\widetilde q$
is called a dominant of (1.2). A dominant $\widetilde q$![]() is called the best dominant if $\widetilde q\prec q$
is called the best dominant if $\widetilde q\prec q$![]() for all dominants $q$
for all dominants $q$![]() of (1.2). Finding those $q$
of (1.2). Finding those $q$![]() for which the subordination (1.2) yields $p\prec q,$
for which the subordination (1.2) yields $p\prec q,$![]() in particular, $p\prec \widetilde q$
in particular, $p\prec \widetilde q$![]() , is the basis in the theory of differential subordinations. Further details and references can be found in the book of Miller and Mocanu [Reference Miller and Mocanu8].
, is the basis in the theory of differential subordinations. Further details and references can be found in the book of Miller and Mocanu [Reference Miller and Mocanu8].
The classical example of (1.2) is related to the arithmetic mean and has been studied by many authors (see e.g., [Reference Miller and Mocanu8, pp. 120–145]). Given $\varphi \in \mathcal {H}(D)$![]() and $\alpha \in [0,\,1],$
and $\alpha \in [0,\,1],$![]() consider
consider
written equivalently as
where $p\in \mathcal {H}$![]() with $p(\mathbb {D})\subset D.$
with $p(\mathbb {D})\subset D.$![]() In particular, if $\alpha =1,$
In particular, if $\alpha =1,$![]() $\delta,\,\gamma \in \mathbb {C},$
$\delta,\,\gamma \in \mathbb {C},$![]() $\delta \not =0,$
$\delta \not =0,$![]() $\varphi (w):=1/(\delta w+\gamma ),\,\ w\in D:=\mathbb {C}\setminus \{-\gamma /\delta \}$
$\varphi (w):=1/(\delta w+\gamma ),\,\ w\in D:=\mathbb {C}\setminus \{-\gamma /\delta \}$![]() , then (1.3) reduces to
, then (1.3) reduces to
which is known as the Briot-Bouquet differential subordination.
Let $\varphi : \mathbb {C}^2\rightarrow \mathbb {C},$![]() $p\in \mathcal {H}[\varphi ]$
$p\in \mathcal {H}[\varphi ]$![]() and $h\in \mathcal {H}$
and $h\in \mathcal {H}$![]() be a convex univalent function which means that $h$
be a convex univalent function which means that $h$![]() maps univalently $\mathbb {D}$
maps univalently $\mathbb {D}$![]() onto a convex domain $h(\mathbb {D}).$
onto a convex domain $h(\mathbb {D}).$![]() In this paper, we propose a study of the differential subordination of the form
In this paper, we propose a study of the differential subordination of the form
The case when $0\in \partial h(\mathbb {D})$![]() has been studied in [Reference Lecko5]. Let us remark that the case where 0 is a boundary point of $h(\mathbb {D})$
has been studied in [Reference Lecko5]. Let us remark that the case where 0 is a boundary point of $h(\mathbb {D})$![]() requires different methods of proofs than those when the origin is the interior point of $h(\mathbb {D}).$
requires different methods of proofs than those when the origin is the interior point of $h(\mathbb {D}).$![]() The differential subordination (1.5) is a special case of (1.2), but it offers interesting applications. In particular, it generalizes the Briot-Bouquet differential subordination (1.4). In addition, we prove in a new way some recent results regarding the differential subordination related to the harmonic mean. The problem of the best dominant in the case where $h$
The differential subordination (1.5) is a special case of (1.2), but it offers interesting applications. In particular, it generalizes the Briot-Bouquet differential subordination (1.4). In addition, we prove in a new way some recent results regarding the differential subordination related to the harmonic mean. The problem of the best dominant in the case where $h$![]() is a linear function is also discussed.
is a linear function is also discussed.
The proof of the main result is based on the original lemma 2.1 on convex univalent functions. Therefore, the proof of Theorem 2.4 is strictly analytical in nature, while until now in the proofs of analogous propositions, analytical arguments have been used in conjunction with geometric considerations (cf. [Reference Miller and Mocanu8]). By applying lemma 2.1, a series of theorems from the monographs [Reference Miller and Mocanu8]) underlying the theory of the differential subordinations can be proved again by using a purely analytical argumentation.
2. Main result
2.1
A function $h\in \mathcal {H}$![]() is said to be convex if it is univalent and $h(\mathbb {D})$
is said to be convex if it is univalent and $h(\mathbb {D})$![]() is a convex domain. Study [Reference Study12] (e.g., [Reference Pommerenke9, p. 44]) has shown that a function $h\in \mathcal {H}$
is a convex domain. Study [Reference Study12] (e.g., [Reference Pommerenke9, p. 44]) has shown that a function $h\in \mathcal {H}$![]() with $h'(0)\not =0$
with $h'(0)\not =0$![]() is convex if, and only if,
is convex if, and only if,
If $h$![]() is a convex function, then $h(\mathbb {D}_r)$
is a convex function, then $h(\mathbb {D}_r)$![]() for every $r\in (0,\,1),$
for every $r\in (0,\,1),$![]() is a convex domain (e.g., [Reference Duren2, p. 42], [Reference Hallenbeck and MacGregor4, p. 14]), so every $h_r,\, r\in (0,\,1),$
is a convex domain (e.g., [Reference Duren2, p. 42], [Reference Hallenbeck and MacGregor4, p. 14]), so every $h_r,\, r\in (0,\,1),$![]() is convex function also. Let $\mathcal {S}^c$
is convex function also. Let $\mathcal {S}^c$![]() be the class of all convex functions normalized by $h(0)=0.$
be the class of all convex functions normalized by $h(0)=0.$![]() For $h\in \mathcal {S}^c$
For $h\in \mathcal {S}^c$![]() the following inequality due to Sheil-Small [Reference Sheil-Small10] and Suffridge [Reference Suffridge13] (see also [Reference Pommerenke9, p. 44]) holds
the following inequality due to Sheil-Small [Reference Sheil-Small10] and Suffridge [Reference Suffridge13] (see also [Reference Pommerenke9, p. 44]) holds
The inequality (2.1) with $z=0$![]() reduces to the inequality
reduces to the inequality
due to Marx [Reference Marx6] and Storhhäcker [Reference Strohhäcker11] (see also [Reference Pommerenke9, p. 45]), which means that $h$![]() is a starlike function of order $1/2$
is a starlike function of order $1/2$![]() (cf. [Reference Goodman3, p. 138]).
(cf. [Reference Goodman3, p. 138]).
Let $\mathcal {Q}$![]() be the subclass of $\mathcal {S}^c$
be the subclass of $\mathcal {S}^c$![]() of all convex functions analytic on $\overline {\mathbb {D}}$
of all convex functions analytic on $\overline {\mathbb {D}}$![]() with $h'(\zeta )\not =0$
with $h'(\zeta )\not =0$![]() at every $\zeta \in \mathbb {T}.$
at every $\zeta \in \mathbb {T}.$![]()
We will now prove the lemma that will be used in the proof of the main theorem. This results is geometrically obvious.
Lemma 2.1 If $h\in \mathcal {Q},$![]() then
then
Proof. Since $h_r$![]() for every $r\in (0,\,1),$
for every $r\in (0,\,1),$![]() is analytic on $\overline {\mathbb {D}}$
is analytic on $\overline {\mathbb {D}}$![]() and convex in $\mathbb {D},$
and convex in $\mathbb {D},$![]() from (2.1) it follows that for $z\in \mathbb {D}$
from (2.1) it follows that for $z\in \mathbb {D}$![]() and $\zeta \in \mathbb {T},$
and $\zeta \in \mathbb {T},$![]()

where $u:=r\zeta \in \mathbb {D}$![]() and $v:=rz\in \mathbb {D}.$
and $v:=rz\in \mathbb {D}.$![]() Hence and by the fact that $h_r(\zeta )\rightarrow h(\zeta )$
Hence and by the fact that $h_r(\zeta )\rightarrow h(\zeta )$![]() and $h_r'(\zeta )\rightarrow h'(\zeta )$
and $h_r'(\zeta )\rightarrow h'(\zeta )$![]() as $r\rightarrow 1^-,$
as $r\rightarrow 1^-,$![]() we deduce that
we deduce that
which shows (2.3).
We need also the following lemma which is a special case of lemma 2.2d [Reference Miller and Mocanu8, p. 22].
Lemma 2.2 Let $h$![]() be an analytic univalent function in $\overline {\mathbb {D}},$
be an analytic univalent function in $\overline {\mathbb {D}},$![]() $p\in \mathcal {H}$
$p\in \mathcal {H}$![]() be a nonconstant function with $p(0)=h(0).$
be a nonconstant function with $p(0)=h(0).$![]() If $p$
If $p$![]() is not subordinate to $h,$
is not subordinate to $h,$![]() then there exist $z_0\in \mathbb {D}\setminus \{0\}$
then there exist $z_0\in \mathbb {D}\setminus \{0\}$![]() and $\zeta _0\in \mathbb {T}$
and $\zeta _0\in \mathbb {T}$![]() such that $p(\mathbb {D}_{|z_0|})\subset h(\mathbb {D}),$
such that $p(\mathbb {D}_{|z_0|})\subset h(\mathbb {D}),$![]()
and
for some $m\ge 1.$![]()
The theorem below follows directly from the Lindelöf Principle (e.g., [Reference Goodman3, Vol. I, p. 86]). However, it will be useful in proving the main theorem.
Theorem 2.3 Let $f,\,h\in \mathcal {H},$![]() $h$
$h$![]() be univalent and $f(0)=h(0).$
be univalent and $f(0)=h(0).$![]() Then
Then
if and only if for every $r\in (0,\,1),$![]()
Proof. Suppose that (2.6) holds. Then by the Lindelöf Principle (e.g., [Reference Goodman3, Vol. I, p. 86]) for every $r\in (0,\,1),$![]()
Since $f_r(0)=f(0)=h(0)=h_r(0)$![]() and every $h_r$
and every $h_r$![]() is univalent, from (1.1) and (2.8) it follows (2.7).
is univalent, from (1.1) and (2.8) it follows (2.7).
Suppose now that (2.7) holds for every $r\in (0,\,1).$![]() Then by (1.1) the inclusion (2.8) holds for every $r\in (0,\,1),$
Then by (1.1) the inclusion (2.8) holds for every $r\in (0,\,1),$![]() and therefore
and therefore
2.2
We now prove the main theorem of this paper. In the proof we apply lemma 2.1 and Theorem 2.3. Therefore the argumentation is purely analytical without using a geometrical property based on the behaviour of the normal vector to the boundary curve $\partial h(\mathbb {D}),$![]() standardly used in the theory (cf. [Reference Miller and Mocanu8]). In further discussion we present new type of the differential subordination generalizing the well known Briot-Bouquet differential subordination. The significance of Theorem 2.4 is emphasized also in the presented applications.
standardly used in the theory (cf. [Reference Miller and Mocanu8]). In further discussion we present new type of the differential subordination generalizing the well known Briot-Bouquet differential subordination. The significance of Theorem 2.4 is emphasized also in the presented applications.
Theorem 2.4 Let $h$![]() be a convex function and $\varphi : \mathbb {C}^2\rightarrow \mathbb {C}$
be a convex function and $\varphi : \mathbb {C}^2\rightarrow \mathbb {C}$![]() be such that for each $m\ge 1$
be such that for each $m\ge 1$![]() a function
a function
is well-defined and analytic satisfying the condition
If $p\in \mathcal {H}[\varphi ]$![]() with $p(0)=h(0),$
with $p(0)=h(0),$![]() and
and
then
Proof. Note first that if $\operatorname {Re} \varphi (h(z_0),\,mz_0h'(z_0))=0$![]() for a certain $z_0\in \mathbb {D},$
for a certain $z_0\in \mathbb {D},$![]() then by the minimum principle for harmonic function $\operatorname {Re} \varphi (h(z),\,mzh'(z))=0$
then by the minimum principle for harmonic function $\operatorname {Re} \varphi (h(z),\,mzh'(z))=0$![]() for all $z\in \mathbb {D}$
for all $z\in \mathbb {D}$![]() and hence $\varphi (h(z),\,mzh'(z))=\mathrm {i} a$
and hence $\varphi (h(z),\,mzh'(z))=\mathrm {i} a$![]() for some $a\in \mathbb {R}$
for some $a\in \mathbb {R}$![]() and all $z\in \mathbb {D}.$
and all $z\in \mathbb {D}.$![]()
Let $p\in \mathcal {H}[\varphi ]$![]() with $p(0)=h(0).$
with $p(0)=h(0).$![]() Define $\psi :\mathbb {D}\rightarrow \mathbb {C}$
Define $\psi :\mathbb {D}\rightarrow \mathbb {C}$![]() as follows
as follows
Since $\psi (0)=p(0)=h(0),$![]() by Theorem 2.3 the condition (2.11) is equivalent to
by Theorem 2.3 the condition (2.11) is equivalent to
On the contrary, suppose that $p$![]() is not subordinate to $h.$
is not subordinate to $h.$![]() By Theorem 2.3, there exists $r_0\in (0,\,1)$
By Theorem 2.3, there exists $r_0\in (0,\,1)$![]() such that $p_{r_0}$
such that $p_{r_0}$![]() is not subordinate to $h_{r_0}.$
is not subordinate to $h_{r_0}.$![]() Since $h_{r_0}$
Since $h_{r_0}$![]() is analytic in $\overline {\mathbb {D}},$
is analytic in $\overline {\mathbb {D}},$![]() by lemma 2.2 there exist $z_0\in \mathbb {D}\setminus \{0\},$
by lemma 2.2 there exist $z_0\in \mathbb {D}\setminus \{0\},$![]() $\zeta _0\in \mathbb {T}$
$\zeta _0\in \mathbb {T}$![]() and $m\ge 1$
and $m\ge 1$![]() such that (2.4) and (2.5) hold with $p:=p_{r_0}$
such that (2.4) and (2.5) hold with $p:=p_{r_0}$![]() and $h:=h_{r_0},$
and $h:=h_{r_0},$![]() i.e.,
i.e.,
and
Hence

Moreover by (2.10),
where $u_0:=r_0\zeta _0\in \mathbb {D}.$![]() In view of (2.14), $\psi _{r_0}\prec h_{r_0}$
In view of (2.14), $\psi _{r_0}\prec h_{r_0}$![]() , so $\psi _{r_0}(\mathbb {D})\subset h_{r_0}(\mathbb {D}).$
, so $\psi _{r_0}(\mathbb {D})\subset h_{r_0}(\mathbb {D}).$![]() Thus $\psi _{r_0}(z_0)\in h_{r_0}(\mathbb {D})$
Thus $\psi _{r_0}(z_0)\in h_{r_0}(\mathbb {D})$![]() and therefore $\psi _{r_0}(z_0)=h_{r_0}(z_1)$
and therefore $\psi _{r_0}(z_0)=h_{r_0}(z_1)$![]() for some $z_1\in h_{r_0}(\mathbb {D}).$
for some $z_1\in h_{r_0}(\mathbb {D}).$![]() Hence from (2.17) and (2.18) we get
Hence from (2.17) and (2.18) we get

Since $h_{r_0}\in \mathcal {Q},$![]() it follows that the above inequality contradicts (2.3) with $h:=h_{r_0},$
it follows that the above inequality contradicts (2.3) with $h:=h_{r_0},$![]() $z:=z_1$
$z:=z_1$![]() and $\zeta :=\zeta _0.$
and $\zeta :=\zeta _0.$![]() Thus we conclude that $\psi _{r_0}$
Thus we conclude that $\psi _{r_0}$![]() is not subordinate to $h_{r_0},$
is not subordinate to $h_{r_0},$![]() which contradicts (2.14) and completes the proof.
which contradicts (2.14) and completes the proof.
In Theorem 2.4 instead of $\varphi$![]() we can put a function $\phi : D\rightarrow \mathbb {C}$
we can put a function $\phi : D\rightarrow \mathbb {C}$![]() such that a function $\mathbb {D}\ni z\mapsto \phi (h(z))$
such that a function $\mathbb {D}\ni z\mapsto \phi (h(z))$![]() is well-defined and analytic satisfying the condition $\operatorname {Re}\phi (h(z))\ge 0$
is well-defined and analytic satisfying the condition $\operatorname {Re}\phi (h(z))\ge 0$![]() for $z\in \mathbb {D}.$
for $z\in \mathbb {D}.$![]() Then we obtain the result due to Miller and Mocanu [Reference Miller and Mocanu7] (see also [Reference Miller and Mocanu8, Theorem 3.4a, p. 120]).
Then we obtain the result due to Miller and Mocanu [Reference Miller and Mocanu7] (see also [Reference Miller and Mocanu8, Theorem 3.4a, p. 120]).
Corollary 2.5 [Reference Miller and Mocanu7]
Let $h$![]() be a convex function, $\phi \in \mathcal {H}(D)$
be a convex function, $\phi \in \mathcal {H}(D)$![]() be such that $h(\mathbb {D})\subset D$
be such that $h(\mathbb {D})\subset D$![]() and
and
If $p\in \mathcal {H},$![]() $p(0)=h(0),$
$p(0)=h(0),$![]() $p(\mathbb {D})\subset D$
$p(\mathbb {D})\subset D$![]() and
and
then
In the following theorem the assumption (2.19) is based on the idea of [Reference Chunfang1] (see also [Reference Miller and Mocanu8, pp. 124–125]), where in the proof of the main result Löwner chains were used. Our argumentation is analogous to that in the proof of Theorem 2.4.
Theorem 2.6 Let $\varphi : \mathbb {C}^2\rightarrow \mathbb {C}$![]() and $p\in \mathcal {H}[\varphi ]$
and $p\in \mathcal {H}[\varphi ]$![]() be such that
be such that
If $h$![]() is a convex function with $h(0)=p(0)$
is a convex function with $h(0)=p(0)$![]() and
and
then
Proof. Let $\psi$![]() be defined as in (2.11). By Theorem 2.3 the condition (2.20) is equivalent to (2.14). On the contrary, suppose that $p$
be defined as in (2.11). By Theorem 2.3 the condition (2.20) is equivalent to (2.14). On the contrary, suppose that $p$![]() is not subordinate to $h.$
is not subordinate to $h.$![]() As in the proof of Theorem 2.4, there exist $z_0\in \mathbb {D}\setminus \{0\},$
As in the proof of Theorem 2.4, there exist $z_0\in \mathbb {D}\setminus \{0\},$![]() $\zeta _0\in \mathbb {T}$
$\zeta _0\in \mathbb {T}$![]() and $m\ge 1$
and $m\ge 1$![]() such that (2.15) and (2.16) hold. Thus
such that (2.15) and (2.16) hold. Thus

where $u_0:=r_0z_0\in \mathbb {D}.$![]() In view of (2.14), $\psi _{r_0}\prec h_{r_0}$
In view of (2.14), $\psi _{r_0}\prec h_{r_0}$![]() , so $\psi _{r_0}(\mathbb {D})\subset h_{r_0}(\mathbb {D}).$
, so $\psi _{r_0}(\mathbb {D})\subset h_{r_0}(\mathbb {D}).$![]() Thus $\psi _{r_0}(z_0)\in h_{r_0}(\mathbb {D})$
Thus $\psi _{r_0}(z_0)\in h_{r_0}(\mathbb {D})$![]() and therefore $\psi _{r_0}(z_0)=h_{r_0}(z_1)$
and therefore $\psi _{r_0}(z_0)=h_{r_0}(z_1)$![]() for some $z_1\in\mathbb{D}.$
for some $z_1\in\mathbb{D}.$![]() Hence from (2.22) and (2.19) it follows that
Hence from (2.22) and (2.19) it follows that

Since $h_{r_0}\in \mathcal {Q},$![]() it follows that the above inequality contradicts (2.3) with $h:=h_{r_0},$
it follows that the above inequality contradicts (2.3) with $h:=h_{r_0},$![]() $z:=z_1$
$z:=z_1$![]() and $\zeta :=\zeta _0.$
and $\zeta :=\zeta _0.$![]() Thus we conclude that $\psi _{r_0}$
Thus we conclude that $\psi _{r_0}$![]() is not subordinate to $h_{r_0},$
is not subordinate to $h_{r_0},$![]() which contradicts (2.14), so (2.20) and completes the proof.
which contradicts (2.14), so (2.20) and completes the proof.
3. Special cases
3.1
We now discuss special cases of Theorem 2.4.
Corollary 3.1 Let $\beta \ge 0,$![]() $h\in \mathcal {S}^c,$
$h\in \mathcal {S}^c,$![]() $\phi \in \mathcal {H}(D)$
$\phi \in \mathcal {H}(D)$![]() be such that $h(\mathbb {D})\subset D$
be such that $h(\mathbb {D})\subset D$![]() and
and
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() $p(\mathbb {D})\subset D$
$p(\mathbb {D})\subset D$![]() and
and
then
Proof. Let $\beta \ge 0,$![]() $h\in \mathcal {S}^c$
$h\in \mathcal {S}^c$![]() and $\phi \in \mathcal {H}(D)$
and $\phi \in \mathcal {H}(D)$![]() be such that $h(\mathbb {D})\subset D.$
be such that $h(\mathbb {D})\subset D.$![]() Define $\varphi :\mathbb {C}\times \mathbb {C}\rightarrow \mathbb {C}$
Define $\varphi :\mathbb {C}\times \mathbb {C}\rightarrow \mathbb {C}$![]() as
as
Since $h(0)=0,$![]() $h(z)\not =0$
$h(z)\not =0$![]() for $z\not =0$
for $z\not =0$![]() and $h'(0)\not =0,$
and $h'(0)\not =0,$![]() it follows that
it follows that
Thus the function
has an analytic extension on $\mathbb {D}$![]() by setting $\phi (0)+\beta m$
by setting $\phi (0)+\beta m$![]() at zero. Moreover by (2.2) and (3.1) for every $m\ge 1,$
at zero. Moreover by (2.2) and (3.1) for every $m\ge 1,$![]()

Let $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\not =0$
for $z\not =0$![]() and $p(\mathbb {D})\subset D.$
and $p(\mathbb {D})\subset D.$![]() Because $p(0)=0,$
Because $p(0)=0,$![]() there exists a positive integer $k$
there exists a positive integer $k$![]() such that $p(z)=z^kq(z),\,\ z\in \mathbb {D},$
such that $p(z)=z^kq(z),\,\ z\in \mathbb {D},$![]() where $q\in \mathcal {H}$
where $q\in \mathcal {H}$![]() and $q(0)\not =0.$
and $q(0)\not =0.$![]() Hence and by the fact that $p(z)\not =0$
Hence and by the fact that $p(z)\not =0$![]() for $z\not =0,$
for $z\not =0,$![]() it follows that $q(z)\not =0$
it follows that $q(z)\not =0$![]() for $z\in \mathbb {D}.$
for $z\in \mathbb {D}.$![]() Thus the function
Thus the function
has an analytic extension on $\mathbb {D}$![]() by setting $\phi (0)+\beta k$
by setting $\phi (0)+\beta k$![]() at zero, i.e., $p\in \mathcal {H}[\varphi ].$
at zero, i.e., $p\in \mathcal {H}[\varphi ].$![]() At the end note that
At the end note that

Thus, the assumptions of Theorem 2.4 are satisfied, which ends the proof of the corollary.
For $\beta =0$![]() the above theorem reduces to Corollary 2.5, with the additional assumption that $h(0)=0$
the above theorem reduces to Corollary 2.5, with the additional assumption that $h(0)=0$![]() . In fact, this assumption is not required in Corollary 2.5.
. In fact, this assumption is not required in Corollary 2.5.
For $\mathcal {H}(\mathbb {C})\ni \phi \equiv \alpha,$![]() where $\operatorname {Re} \alpha \ge 0,$
where $\operatorname {Re} \alpha \ge 0,$![]() Corollary 3.1 takes the following form.
Corollary 3.1 takes the following form.
Corollary 3.2 Let $\alpha \in \mathbb {C},\,\ \operatorname {Re}\alpha \ge 0,$![]() $\beta \ge 0$
$\beta \ge 0$![]() and $h\in \mathcal {S}^c.$
and $h\in \mathcal {S}^c.$![]() If $p\in \mathcal {H},$
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() and
and
then
For $\alpha =0$![]() from Corollary 3.2 we deduce
from Corollary 3.2 we deduce
Corollary 3.3 Let $\beta \ge 0$![]() and $h\in \mathcal {S}^c.$
and $h\in \mathcal {S}^c.$![]() If $p\in \mathcal {H},$
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() and
and
then
The differential subordination (3.9), which is a special case of (3.2), is an interesting generalization of the Briot-Bouqet subordination. Briot-Bouquet differential subordination plays a fundamental role in the theory of the differential subordinations. We get it from (3.9) for $\beta =0$![]() (e.g. [Reference Miller and Mocanu8, pp. 80–105]). The following corollary follows from Corollary 3.1.
(e.g. [Reference Miller and Mocanu8, pp. 80–105]). The following corollary follows from Corollary 3.1.
Corollary 3.4 Let $\beta \ge 0,$![]() $\delta,\,\gamma \in \mathbb {C},$
$\delta,\,\gamma \in \mathbb {C},$![]() $\delta \not =0,$
$\delta \not =0,$![]() and $h\in \mathcal {S}^c$
and $h\in \mathcal {S}^c$![]() be such that
be such that
and
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() $p(z)\not =-\gamma /\delta$
$p(z)\not =-\gamma /\delta$![]() for $z\in \mathbb {D},$
for $z\in \mathbb {D},$![]() and
and
then
Proof. Take
Then by (3.7) the function $\phi \circ h$![]() is analytic in $\mathbb {D},$
is analytic in $\mathbb {D},$![]() and by (3.8),
and by (3.8),
and we apply Corollary 3.1.
In the same way as Corollary 3.4 the following result follows.
Corollary 3.5 Let $\beta \ge 0,$![]() $\delta,\,\gamma \in \mathbb {C},$
$\delta,\,\gamma \in \mathbb {C},$![]() $\delta \not =0,$
$\delta \not =0,$![]() and $h\in \mathcal {S}^c$
and $h\in \mathcal {S}^c$![]() be such that
be such that
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() and
and
then
3.2
By selecting $h\in \mathcal {S}^c$![]() we can get a number of new results. It is natural to take into account the following convex functions keeping the origin fixed: for $M>0,$
we can get a number of new results. It is natural to take into account the following convex functions keeping the origin fixed: for $M>0,$![]()

Then Corollary 3.1 takes respectively the form
Corollary 3.6 Let $\beta \ge 0,$![]() $\phi \in \mathcal {H}(D)$
$\phi \in \mathcal {H}(D)$![]() be such that $\mathbb {D}_M\subset D$
be such that $\mathbb {D}_M\subset D$![]() and
and
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() $p(\mathbb {D})\subset D$
$p(\mathbb {D})\subset D$![]() and
and

then
Corollary 3.7 Let $\beta \ge 0,$![]() $\phi \in \mathcal {H}(D)$
$\phi \in \mathcal {H}(D)$![]() be such that $A:=\{w\in \mathbb {C}: \operatorname {Re} w>-M\} \subset D$
be such that $A:=\{w\in \mathbb {C}: \operatorname {Re} w>-M\} \subset D$![]() and
and
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() $p(\mathbb {D})\subset D$
$p(\mathbb {D})\subset D$![]() and
and

then
Corollary 3.8 Let $\beta \ge 0,$![]() $\phi \in \mathcal {H}(D)$
$\phi \in \mathcal {H}(D)$![]() be such that $A:=\{w\in \mathbb {C}: |\operatorname {Im} w|< M\} \subset D$
be such that $A:=\{w\in \mathbb {C}: |\operatorname {Im} w|< M\} \subset D$![]() and
and
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() $p(\mathbb {D})\subset D$
$p(\mathbb {D})\subset D$![]() and
and

then
4. The best dominant
To find the best dominant of (2.12) is an interesting problem to study related to the theory of the differential equations. By applying Theorem 2.3e of [Reference Miller and Mocanu8] we can expect that the best dominant $\widetilde {q}$![]() of (1.5) should be a univalent solution of the differential equation
of (1.5) should be a univalent solution of the differential equation
if such a solution exists. Here we restrict our interest to the differential subordination (3.6) with $h(z):=Mz,\,\ z\in \mathbb {D},$![]() where $M>0.$
where $M>0.$![]() For this purpose, we will find a univalent solution of the differential equation
For this purpose, we will find a univalent solution of the differential equation
The following theorem provides a solution to this problem.
Theorem 4.1 Let $\alpha \in \mathbb {C},\,\ \operatorname {Re}\alpha \ge 0,\,\ \beta \ge 0$![]() and $M>0.$
and $M>0.$![]() If $p\in \mathcal {H},$
If $p\in \mathcal {H},$![]() $p(0)=0,$
$p(0)=0,$![]() $p(z)\not =0$
$p(z)\not =0$![]() for $z\in \mathbb {D}\setminus \{0\},$
for $z\in \mathbb {D}\setminus \{0\},$![]() and
and
then
and $\widetilde {q}$![]() is the best dominant of (4.2).
is the best dominant of (4.2).
Proof. We apply the technique of power series to find a univalent solution of (4.1) of the form

Since $q$![]() is assumed to be univalent, we see that
is assumed to be univalent, we see that
From (4.1) we equivalently have
Hence using (4.3) we have

Comparing coefficients we obtain

and in general, for $n=2k-1,\,\ k\ge 2,$![]()

and for $n=2k,\,\ k\ge 2,$![]()

Taking into account (4.4) from the first equation in (4.5) it follows that
This and the second equation in (4.5) yield $a_2=0.$![]() Substituting $a_2=0$
Substituting $a_2=0$![]() into the third equation in (4.5) in view of (4.8) we see that $a_3=0.$
into the third equation in (4.5) in view of (4.8) we see that $a_3=0.$![]() In this way, by using mathematical induction we can prove that
In this way, by using mathematical induction we can prove that
and that the formula (4.6) reduces to
which in view of (4.8) yield $a_{2k-2}=0.$![]() Hence by using (4.9) the equation (4.7) reduces to
Hence by using (4.9) the equation (4.7) reduces to
which in view of (4.8) yield $a_{2k-1}=0.$![]() Thus we proved that $a_n=0$
Thus we proved that $a_n=0$![]() for all $n\ge 2.$
for all $n\ge 2.$![]() In this way by (4.3) and (4.8) we see that
In this way by (4.3) and (4.8) we see that
is a unique univalent solution of (4.1). From Theorem 2.3e of [Reference Miller and Mocanu8] it follows that $\widetilde {q}$![]() is the best dominant of (4.2) which completes the proof of the lemma.
is the best dominant of (4.2) which completes the proof of the lemma.
For $\alpha =1,$![]() $\beta =1$
$\beta =1$![]() and $M=1,$
and $M=1,$![]() the above result reduces to the well known special case of the first order Euler differential subordination (see [Reference Miller and Mocanu8, pp. 334–340]).
the above result reduces to the well known special case of the first order Euler differential subordination (see [Reference Miller and Mocanu8, pp. 334–340]).
Corollary 4.2 If $p\in \mathcal {H},$![]() $p(0)=0$
$p(0)=0$![]() and
and
then
and $\widetilde {q}$![]() is the best dominant.
is the best dominant.