Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-28T02:59:23.903Z Has data issue: false hasContentIssue false
  • English
  • Français

Multipliers for vector valued functions

Published online by Cambridge University Press:  14 November 2011

José Luis Torrea
José Luis Torrea
Affiliation:
Division de Matematicas, Universidad Autonoma de Madrid, Canto Blanco, Madrid 34, Spain
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a locally compact abelian group and let Γ be the dual of G. Let A, B be Banach spaces and Lp(G,A) the Bochner-Lebesgue spaces. We prove that the space of bounded linear translation invariant operators from L1(G, A) to LX(G, B) can be identified with the space of bounded convolution invariant (in some sense) operators and also with the space of a(A, B)-valued “weak regular” measures with the relation Tf = f *μ. (A. The existence of a function m∈ L∞ (Γ,α(A,B)), such that 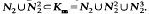is also proved.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 99 , Issue 1-2 , 1984 , pp. 137 - 143
Copyright
Copyright © Royal Society of Edinburgh 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Diestel, J. and Uhl, J. J.. Vector Measures (A.M.S. Surveys 15) (Providence, R.I.: Amer. Math. Soc, 1977).CrossRefGoogle Scholar
2Dinculeanu, N.. Vector Measures (London: Pergamon, 1967).CrossRefGoogle Scholar
3Chan, Ming-Kam. Characterisations of the right multipliers for L 1(GA). Proc. Edinburgh Math. Soc. 22 (1979), 181–186.CrossRefGoogle Scholar
4Francia, J. L. Rubio de and Torrea, J. L.. Type, cotype and extension properties of Banach spaces, preprint.Google Scholar
5Rudin, W.. Fourier Analysis on Groups (New York: Wiley, 1967).Google Scholar
6Ruiz, F. J. and Torrea, J. L.. Transformada de Fourier de funciones vectoriales. Rev. Real Acad. Gene. Madrid 75 (1981), 707–717.Google Scholar
7Singer, I.. Linear functionals on the space of continuous mapping of a compact Hausdorff space into a Banach space. Rev. Math. Pures Appl. 2 (1957), 301–305.Google Scholar
8Tewari, U. B., Dutta, M. and Waidya, D. P.. Multipliers of group algebras of vector-valued functions. Proc. Amer. Math. Soc. 81 (1981), 223–229.CrossRefGoogle Scholar
9Torrea, J. L.. Andlisis de Fourier de Functiones vectoriales. Ph.D. Dissertation, Zaragoza, 1980.Google Scholar