Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bertotti, Maria Letizia
and
Montecchiari, Piero
1998.
Connecting Orbits for Some Classes of Almost Periodic Lagrangian Systems.
Journal of Differential Equations,
Vol. 145,
Issue. 2,
p.
453.
Zhang, Shiqing
2000.
Symmetrically Homoclinic Orbits for Symmetric Hamiltonian Systems.
Journal of Mathematical Analysis and Applications,
Vol. 247,
Issue. 2,
p.
645.
Zhu, Wenzhuang
2012.
Existence of homoclinic solutions for a class of second order systems.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 75,
Issue. 4,
p.
2455.
Izydorek, Marek
and
Janczewska, Joanna
2014.
Two families of infinitely many homoclinics for singular strong force Hamiltonian systems.
Journal of Fixed Point Theory and Applications,
Vol. 16,
Issue. 1-2,
p.
301.
Costa, David G.
and
Tehrani, Hossein
2014.
On a class of singular second-order Hamiltonian systems with infinitely many homoclinic solutions.
Journal of Mathematical Analysis and Applications,
Vol. 412,
Issue. 1,
p.
200.
Zhang, Ziheng
Liao, Fang-Fang
and
Wong, Patricia J. Y.
2014.
Homoclinic Solutions for a Class of Second Order Nonautonomous Singular Hamiltonian Systems.
Abstract and Applied Analysis,
Vol. 2014,
Issue. ,
p.
1.
Boughariou, Morched
and
Mahmoud, Marouen
2025.
Homoclinic solutions for a class of second-order singular Hamiltonian systems.
Journal of Mathematical Analysis and Applications,
Vol. 549,
Issue. 1,
p.
129535.


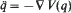 , with
, with 