Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Berkovits, Juha
2001.
On the Leray–Schauder Formula and Bifurcation.
Journal of Differential Equations,
Vol. 173,
Issue. 2,
p.
451.
Berkovits, Juha
2003.
On the bifurcation of large amplitude solutions for a system of wave and beam equations.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 52,
Issue. 1,
p.
343.
Yan, Long
Ji, Shuguan
and
Sun, Lili
2020.
Asymptotic bifurcation results for coupled nonlinear wave equations with variable coefficients.
Journal of Differential Equations,
Vol. 269,
Issue. 9,
p.
7157.
Dinca, George
and
Mawhin, Jean
2021.
Brouwer Degree.
Vol. 95,
Issue. ,
p.
77.


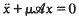 where
where 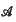 is a (not necessarily diagonal) matrix and one relates the computation of a general multiplicity defined from this system to the corresponding multiplicity of some eigenvalues of
is a (not necessarily diagonal) matrix and one relates the computation of a general multiplicity defined from this system to the corresponding multiplicity of some eigenvalues of 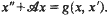 .
.