Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chen, Wenjing
and
Gui, Yuyan
2021.
Existence and multiplicity of solutions for fractional Laplacian system.
Applicable Analysis,
Vol. 100,
Issue. 6,
p.
1327.
Guo, Zhenyu
and
Deng, Yan
2022.
Ground state solutions for a fractional system involving critical non-linearities.
Annals of Functional Analysis,
Vol. 13,
Issue. 3,
Zhu, Qinghao
Qi, Jianming
and
Feng, Baowei
2023.
Critical Fractional
p
-Laplacian System with Negative Exponents.
Journal of Function Spaces,
Vol. 2023,
Issue. ,
p.
1.
Da Silva, João Pablo P.
2023.
Existence of non-negative solutions for a system with concave-convex nonlinearity.
Journal of Elliptic and Parabolic Equations,
Vol. 9,
Issue. 2,
p.
1319.
Echarghaoui, Rachid
and
Sersif, Rachid
2023.
Infinitely many solutions for a double critical Sobolev problem with concave nonlinearities.
Journal of Elliptic and Parabolic Equations,
Vol. 9,
Issue. 2,
p.
1245.
Da Silva, João Pablo P.
2024.
W 0 1 , p ( Ω ) × W 0 1 , p ( Ω ) versus C 0 1 ( Ω ) × C 0 1 ( Ω ) local minimizers.
Asymptotic Analysis,
Vol. 140,
Issue. 1-2,
p.
59.
Zhang, Shulin
2024.
Existence and Multiplicity of Solutions for Fractional p-Laplacian Systems Involving Critical Homogeneous Nonlinearities.
Symmetry,
Vol. 17,
Issue. 1,
p.
21.
El-Houari, Hamza
Moussa, Hicham
and
Sabiki, Hajar
2024.
Fractional Musielak spaces: a class of non-local elliptic system involving generalized nonlinearity.
Rendiconti del Circolo Matematico di Palermo Series 2,
Vol. 73,
Issue. 7,
p.
2547.
Ye, Dong
and
Zhang, Weimin
2024.
Existence and multiplicity of solutions for fractional p-Laplacian equation involving critical concave-convex nonlinearities.
Advanced Nonlinear Studies,
Vol. 24,
Issue. 4,
p.
895.
Santos, Gelson C. G. dos
Medeiros, Aldo H. S.
and
Figueiredo Sousa, Tarcyana S.
2024.
Solution for nonvariational fractional elliptic system with concave and convex nonlinearities.
Zeitschrift für angewandte Mathematik und Physik,
Vol. 75,
Issue. 4,
Pinheiro Da Silva, João Pablo
2025.
Existence and non-existence results for a class of systems under concave-convex nonlinearities.
Proceedings of the Edinburgh Mathematical Society,
Vol. 68,
Issue. 1,
p.
128.
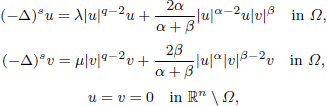
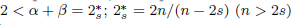 is the fractional critical Sobolev exponent.
is the fractional critical Sobolev exponent.