Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T02:39:18.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Multi-clustered solutions for a singularly perturbed forced pendulum equation

Part of: Asymptotic theory General theory in ordinary differential equations

Published online by Cambridge University Press:  26 January 2019

Salomé Martínez  and
Dora Salazar
Salomé Martínez
Affiliation:
Departamento de Ingeniería Matemática and Centro de Modelamiento Matemático, UMI 2807 CNRS, Universidad de Chile, Beauchef 851, Edificio Norte–Piso 5, Santiago, Chile ([email protected])
Dora Salazar
Affiliation:
Escuela de Matemáticas, Universidad Nacional de Colombia Sede Medellín, Apartado Aéreo 3840, Medellín, Colombia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we are concerned with unbounded solutions of the singularly perturbed forced pendulum equation in the presence of friction, namely

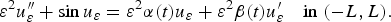$$\varepsilon ^2u_\varepsilon ^{{\prime}{\prime}} + \sin u_\varepsilon = \varepsilon ^2\alpha (t)u_\varepsilon + \varepsilon ^2\beta (t)u_\varepsilon ^{\prime} \quad {\rm in}\;(-L,L).{\rm }$$
Using a limiting energy function, we describe the behaviour of the solutions as the parameter ε approaches zero. We also prove the existence of a family of solutions having a prescribed asymptotic profile and exhibiting a highly rotatory behaviour alternated with a highly oscillatory behaviour in some open subsets of the domain. The proof relies on a combination of the Nehari finite dimensional reduction with the topological degree theory.

Keywords

forced pendulum equationunbounded solutions

MSC classification

Primary: 34A12: Initial value problems, existence, uniqueness, continuous dependence and continuation of solutions
Secondary: 34E15: Singular perturbations, general theory 34E10: Perturbations, asymptotics
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 1 , February 2020 , pp. 387 - 417
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Felmer, P. and Martínez, S. Thick clusters for the radially symmetric nonlinear Schrdinger equation. Calc. Var. Partial Differ. Equ. 31 (2008), 231–261.CrossRefGoogle Scholar
2Felmer, P., Martínez, S. and Tanaka, K. Multi-clustered high-energy solutions for a phase transition problem. Proc. R. Soc. Edinb. A 135 (2005), 731–765.CrossRefGoogle Scholar
3Felmer, P., Martínez, S. and Tanaka, K. High frequency solutions for the singularly perturbed one-dimensional nonlinear Schrodinger equation. Arch. Ration. Mech. Anal. 182 (2006), 333–366.CrossRefGoogle Scholar
4Felmer, P., de Laire, A., Martínez, S. and Tanaka, K. High energy rotation type solutions of the forced pendulum equation. Nonlinearity 26 (2013), 1473–1499.CrossRefGoogle Scholar
5Hastings, S. P. Use of “simple shooting” to obtain chaos. Homoclinic chaos (Brussels, 1991). Phys. D 62 (1993), 87–93.CrossRefGoogle Scholar
6Hastings, S. P. and McLeod, J. B. Chaotic motion of a pendulum with oscillatory forcing. Amer. Math. Monthly 100 (1993), 563–572.CrossRefGoogle Scholar
7Hastings, S. P. and McLeod, J. B. Classical methods in ordinary differential equations with applications to boundary value problems. Graduate Studies in Mathematics, vol. 129 (AMS, Providence, RI, 2012).Google Scholar
8Mawhin, J.. Seventy-five years of global analysis around the forced pendulum equation. Proc. EQUADIFF 9 (1997), 115–145, (CD ROM).Google Scholar
9Mawhin, J.. Global results for the forced pendulum equation. In Handbook of Differential Equations, pp. 533–589 (Amsterdam: Elsevier/North-Holland, 2004).Google Scholar
10Wiggins, S. On the detection and dynamical consequences of orbits homoclinic to hyperbolic periodic orbits and normally hyperbolic invariant tori in a class of ordinary differential equations. SIAM J. Appl. Math. 48 (1988), 262–285.CrossRefGoogle Scholar