No CrossRef data available.
Published online by Cambridge University Press: 29 August 2023
This paper mainly concerns the KAM persistence of the mapping $\mathscr {F}:\mathbb {T}^{n}\times E\rightarrow \mathbb {T}^{n}\times \mathbb {R}^{n}$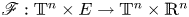 with intersection property, where $E\subset \mathbb {R}^{n}$
with intersection property, where $E\subset \mathbb {R}^{n}$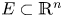 is a connected closed bounded domain with interior points. By assuming that the frequency mapping satisfies certain topological degree condition and weak convexity condition, we prove some Moser-type results about the invariant torus of mapping $\mathscr {F}$
is a connected closed bounded domain with interior points. By assuming that the frequency mapping satisfies certain topological degree condition and weak convexity condition, we prove some Moser-type results about the invariant torus of mapping $\mathscr {F}$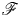 with frequency-preserving under small perturbations. To our knowledge, this is the first approach to Moser's theorem with frequency-preserving. Moreover, given perturbed mappings over $\mathbb {T}^n$
with frequency-preserving under small perturbations. To our knowledge, this is the first approach to Moser's theorem with frequency-preserving. Moreover, given perturbed mappings over $\mathbb {T}^n$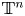 , it is shown that such persistence still holds when the frequency mapping and perturbations are only continuous about parameter beyond Lipschitz or even Hölder type. We also touch the parameter without dimension limitation problem under such settings.
, it is shown that such persistence still holds when the frequency mapping and perturbations are only continuous about parameter beyond Lipschitz or even Hölder type. We also touch the parameter without dimension limitation problem under such settings.