We study the asymptotic properties of blow-up solutions u = u(x, t) ≥ 0 of the quasilinear heat equation 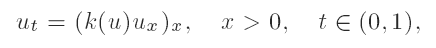, where k(u) is a smooth non-negative function, with a given blowing up regime on the boundary u(0, t) = ψ(t) > 0 for t ∈ (0, 1), where ψ(t) → ∞ as t → 1−, and bounded initial data u(x, 0) ≥ 0. We classify the asymptotic properties of the solutions near the blow-up time, t → 1−, in terms of the heat conductivity coefficient k(u) and of boundary data ψ(t); both are assumed to be monotone. We describe a domain, denoted by , of minimal asymptotics corresponding to the data ψ(t) with a slow growth as t → 1− and a class of nonlinear coefficients k(u).

We prove that for any problem in S11−, such a blow-up singularity is asymptotically structurally equivalent to a singularity of the heat equation ut = uxx described by its self-similar solution of the form u*(x, t) = −ln(1 − t) + g(ξ), ξ = x/(1 − t)1/2, where g solves a linear ordinary differential equation. This particular self-similar solution is structurally stable upon perturbations of the boundary function and also upon nonlinear perturbations of the heat equation with the basin of attraction .