No CrossRef data available.
Published online by Cambridge University Press: 27 August 2024
Let $m,\,r\in {\mathbb {Z}}$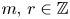 and $\omega \in {\mathbb {R}}$
and $\omega \in {\mathbb {R}}$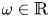 satisfy $0\leqslant r\leqslant m$
satisfy $0\leqslant r\leqslant m$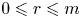 and $\omega \geqslant 1$
and $\omega \geqslant 1$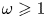 . Our main result is a generalized continued fraction for an expression involving the partial binomial sum $s_m(r) = \sum _{i=0}^r\binom{m}{i}$
. Our main result is a generalized continued fraction for an expression involving the partial binomial sum $s_m(r) = \sum _{i=0}^r\binom{m}{i}$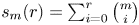 . We apply this to create new upper and lower bounds for $s_m(r)$
. We apply this to create new upper and lower bounds for $s_m(r)$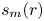 and thus for $g_{\omega,m}(r)=\omega ^{-r}s_m(r)$
and thus for $g_{\omega,m}(r)=\omega ^{-r}s_m(r)$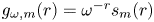 . We also bound an integer $r_0 \in \{0,\,1,\,\ldots,\,m\}$
. We also bound an integer $r_0 \in \{0,\,1,\,\ldots,\,m\}$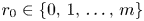 such that $g_{\omega,m}(0)<\cdots < g_{\omega,m}(r_0-1)\leqslant g_{\omega,m}(r_0)$
such that $g_{\omega,m}(0)<\cdots < g_{\omega,m}(r_0-1)\leqslant g_{\omega,m}(r_0)$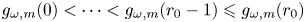 and $g_{\omega,m}(r_0)>\cdots >g_{\omega,m}(m)$
and $g_{\omega,m}(r_0)>\cdots >g_{\omega,m}(m)$ . For real $\omega \geqslant \sqrt 3$
. For real $\omega \geqslant \sqrt 3$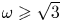 we prove that $r_0\in \{\lfloor \frac {m+2}{\omega +1}\rfloor,\,\lfloor \frac {m+2}{\omega +1}\rfloor +1\}$
we prove that $r_0\in \{\lfloor \frac {m+2}{\omega +1}\rfloor,\,\lfloor \frac {m+2}{\omega +1}\rfloor +1\}$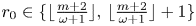 , and also $r_0 =\lfloor \frac {m+2}{\omega +1}\rfloor$
, and also $r_0 =\lfloor \frac {m+2}{\omega +1}\rfloor$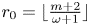 for $\omega \in \{3,\,4,\,\ldots \}$
for $\omega \in \{3,\,4,\,\ldots \}$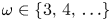 or $\omega =2$
or $\omega =2$ and $3\nmid m$
and $3\nmid m$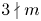 .
.