Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Heo , Yaryong
2016.
Multi-Parameter Maximal Operators Associated with Finite Measures and Arbitrary Sets of Parameters.
Integral Equations and Operator Theory,
Vol. 86,
Issue. 2,
p.
185.
Hughes, Kevin
2017.
Restricted weak-type endpoint estimates for k-spherical maximal functions.
Mathematische Zeitschrift,
Vol. 286,
Issue. 3-4,
p.
1303.
Heo, Yaryong
Hong, Sunggeum
and
Yang, Chan Woo
2018.
Maximal Averages over Certain Non-smooth and Non-convex Hypersurfaces.
Taiwanese Journal of Mathematics,
Vol. 22,
Issue. 6,
Beltran, David
Roos, Joris
and
Seeger, Andreas
2024.
Multi-scale Sparse Domination.
Memoirs of the American Mathematical Society,
Vol. 298,
Issue. 1491,
Borges, Tainara
and
Foster, Benjamin
2024.
Bounds for Lacunary Bilinear Spherical and Triangle Maximal Functions.
Journal of Fourier Analysis and Applications,
Vol. 30,
Issue. 5,
Borges, Tainara
Foster, Benjamin
and
Ou, Yumeng
2025.
Sobolev smoothing estimates for bilinear maximal operators with fractal dilation sets.
Journal of Functional Analysis,
Vol. 288,
Issue. 2,
p.
110694.


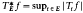 , where
, where 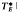 being the maximal operator associated to a convex body, we prove that the norm of the operator is independent of the body.
being the maximal operator associated to a convex body, we prove that the norm of the operator is independent of the body.