No CrossRef data available.
Published online by Cambridge University Press: 08 March 2022
We consider the following inhomogeneous problems
\[ \begin{cases} \epsilon^{2}\mbox{div}(a(x)\nabla u(x))+f(x,u)=0 & \text{ in }\Omega,\\ \frac{\partial u}{\partial \nu}=0 & \text{ on }\partial \Omega,\\ \end{cases} \]
where $\Omega$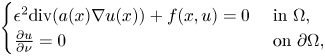
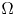 is a smooth and bounded domain in general dimensional space $\mathbb {R}^{N}$
is a smooth and bounded domain in general dimensional space $\mathbb {R}^{N}$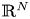 , $\epsilon >0$
, $\epsilon >0$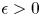 is a small parameter and function $a$
is a small parameter and function $a$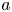 is positive. We respectively obtain the locations of interior transition layers of the solutions of the above transition problems that are $L^{1}$
is positive. We respectively obtain the locations of interior transition layers of the solutions of the above transition problems that are $L^{1}$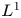 -local minimizer and global minimizer of the associated energy functional.
-local minimizer and global minimizer of the associated energy functional.