Published online by Cambridge University Press: 01 October 2010
We study the homogenization and localization of high-frequency waves in a locally periodic media with period ε. We consider initial data that are localized Bloch-wave packets, i.e. that are the product of a fast oscillating Bloch wave at a given frequency ξ and of a smooth envelope function whose support is concentrated at a point x with length scale 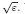 . We assume that (ξ, x) is a stationary point in the phase space of the Hamiltonian λ(ξ, x), i.e. of the corresponding Bloch eigenvalue. Upon rescaling at size
. We assume that (ξ, x) is a stationary point in the phase space of the Hamiltonian λ(ξ, x), i.e. of the corresponding Bloch eigenvalue. Upon rescaling at size 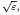 we prove that the solution of the wave equation is approximately the sum of two terms with opposite phases which are the product of the oscillating Bloch wave and of two limit envelope functions which are the solution of two Schrödinger type equations with quadratic potential. Furthermore, if the full Hessian of the Hamiltonian λ(ξ, x) is positive definite, then localization takes place in the sense that the spectrum of each homogenized Schrödinger equation is made of a countable sequence of finite multiplicity eigenvalues with exponentially decaying eigenfunctions.
we prove that the solution of the wave equation is approximately the sum of two terms with opposite phases which are the product of the oscillating Bloch wave and of two limit envelope functions which are the solution of two Schrödinger type equations with quadratic potential. Furthermore, if the full Hessian of the Hamiltonian λ(ξ, x) is positive definite, then localization takes place in the sense that the spectrum of each homogenized Schrödinger equation is made of a countable sequence of finite multiplicity eigenvalues with exponentially decaying eigenfunctions.