Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Plonka, G.
and
Zhou, D.-X.
2003.
Properties of locally linearly independent refinable function vectors.
Journal of Approximation Theory,
Vol. 122,
Issue. 1,
p.
24.
Sun, Qiyu
2010.
Local reconstruction for sampling in shift-invariant spaces.
Advances in Computational Mathematics,
Vol. 32,
Issue. 3,
p.
335.
Dai, XinRong
and
Song, JunQuan
2011.
Summation and intersection of refinable shift invariant spaces.
Science China Mathematics,
Vol. 54,
Issue. 10,
p.
2087.
JIA, RONG-QING
2013.
UNCONDITIONAL CONVERGENCE AND UNCONDITIONAL BASES IN HARDY SPACES.
Analysis and Applications,
Vol. 11,
Issue. 04,
p.
1350016.
Han, Bin
2017.
Framelets and Wavelets.
p.
371.
Han, Bin
2017.
Framelets and Wavelets.
p.
1.
Han, Bin
2017.
Framelets and Wavelets.
p.
485.
Han, Bin
2017.
Framelets and Wavelets.
p.
245.
Han, Bin
2017.
Framelets and Wavelets.
p.
67.
Han, Bin
2017.
Framelets and Wavelets.
p.
153.
Han, Bin
2017.
Framelets and Wavelets.
p.
579.
Cheng, Cheng
and
Sun, Qiyu
2021.
Stable Phaseless Sampling and Reconstruction of Real-Valued Signals with Finite Rate of Innovation.
Acta Applicandae Mathematicae,
Vol. 171,
Issue. 1,

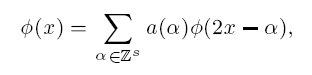 where a is a finitely supported sequence of r × r matrices called the refinement mask. A complete characterization for the local linear independence of the shifts of ϕ1,…,ϕr is given strictly in terms of the mask. Several examples are provided to illustrate the general theory. This investigation is important for construction of wavelets on bounded domains and nonlinear approximation by wavelets.
where a is a finitely supported sequence of r × r matrices called the refinement mask. A complete characterization for the local linear independence of the shifts of ϕ1,…,ϕr is given strictly in terms of the mask. Several examples are provided to illustrate the general theory. This investigation is important for construction of wavelets on bounded domains and nonlinear approximation by wavelets.