Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tarkhanov, N. N.
1985.
Analog of the Painlev� theorem for elliptic systems.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 37,
Issue. 4,
p.
308.
Hile, G. N.
and
Zhou, Chiping
1999.
Liouville theorems for elliptic systems of arbitrary order.
Applicable Analysis,
Vol. 73,
Issue. 1-2,
p.
115.


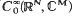 .
.