Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T02:00:01.054Z Has data issue: false hasContentIssue false
  • English
  • Français

Large-time behaviour of solutions of a reaction–diffusion equation

Published online by Cambridge University Press:  14 November 2011

Arturo de Pablo
Arturo de Pablo
Affiliation:
Departamento de Ingeniería Industrial, Escuela Politécnica Superior, Universidad Carlos III de Madrid, 28913 Leganés, Spain
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the large-time behaviour of the solutions u = u(x, t) to the one-dimensional nonlinear heat equation with reaction

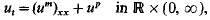
with exponents m > 1,p < 1. The initial function u(x, 0) is assumed to be measurable and nonnegative. In the case m + p ≧ 2 where the initial value does not uniquely determine the solution, we also fix the positivity set of the solution u(x, t) if the support of u(x, 0) is not the whole line ℝ, i.e. u(x, t) > 0 if and only if −s1(t) <x<s2(t), t ≧ 0, where 0≦si(t)≦∞ for t ≧ 0, i = 1, 2 are lower semicontinuous given functions. We prove that u converges to a self-similar function which depends only on the behaviour of u(x, 0) for |x| large or si(t) for t large. We classify the set of self-similar solutions and study the equation satisfied by their interfaces.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 2 , 1994 , pp. 389 - 398
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Aguirre, J. and Escobedo, M.. A Cauchy problem for ut, = Δu + up with 0 < p < 1. Asymptotic behaviour of solutions. Ann. Fac. Sci. Toulouse Math. (5) 8 (1986), 175–203.CrossRefGoogle Scholar
2di, E.Benedetto. Continuity of weak solutions to a general porous medium equation. Indiana Univ. Mart. J. 32(1983), 83–118.Google Scholar
3Escobedo, M. and Zuazua, E.. Large time behavior for convection-diffusion equations in RN. J. Fund. Anal. 100(1991), 119–161.CrossRefGoogle Scholar
4Friedman, A. and Kamin, S.. The asymptotic behaviour of gas in an n-dimensional porous medium. Trans. Amer. Math. Soc. 262 (1980), 551–563.Google Scholar
5Galaktionov, V. and Vazquez, J. L.. Asymptotic behaviour of nonlinear parabolic equations with critical exponents. A dynamical systems approach. J. Fund. Anal. 100 (1991), 435–462.CrossRefGoogle Scholar
6Gmira, A. and Veron, L.. Large time behaviour of the solutions of a semilinear parabolic equation in RN. J. Differential Equations 53 (1989), 258–276.CrossRefGoogle Scholar
7Kamin, S. and Peletier, L. A.. Large-time behaviour of the heat equation with absorption. Ann. Scuola Norm. Sup. Pisa 12 (1985), 393–408.Google Scholar
8Kamin, S. and Peletier, L. A.. Large-time behaviour of the porous medium equation with absorption. Israel J. Math. 55 (1986), 129–146.CrossRefGoogle Scholar
9Kamin, S. and Vazquez, J. L.. Fundamental solutions asymptotic behaviour for the p-laplacian equation. Rev. Mat. Iberoamericana 4 (1988), 339–354.CrossRefGoogle Scholar
10Knerr, B. F.. The porous medium equation in one dimension. Trans. Amer. Math. Soc. 234 (1977), 381–415.Google Scholar
11de Pablo, A. and Vazquez, J. L.. Balance between strong reaction and slow diffusion. Comm. Partial Differential Equations 15 (1990), 159–183.CrossRefGoogle Scholar
12de Pablo, A. and Vazquez, J. L.. Travelling waves and finite propagation in a reaction–diffusion equation. J. Differential Equations 93 (1991), 19–61.Google Scholar
13de Pablo, A. and Vazquez, J. L.. An overdetermined initial and boundary-value problem for a reaction–diffusion equation. J. Nonlinear Anal. 19 (1992), 259–269.CrossRefGoogle Scholar