Article contents
Jump phenomena of the n-th eigenvalue of discrete Sturm–Liouville problems with application to the continuous case
Published online by Cambridge University Press: 02 March 2022
Abstract
In this paper, we characterize jump phenomena of the $n$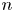 -th eigenvalue of self-adjoint discrete Sturm–Liouville problems in any dimension. For a fixed Sturm–Liouville equation, we completely characterize jump phenomena of the $n$
-th eigenvalue of self-adjoint discrete Sturm–Liouville problems in any dimension. For a fixed Sturm–Liouville equation, we completely characterize jump phenomena of the $n$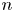 -th eigenvalue. For a fixed boundary condition, unlike in the continuous case, the $n$
-th eigenvalue. For a fixed boundary condition, unlike in the continuous case, the $n$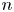 -th eigenvalue exhibits jump phenomena and we describe the singularity under a non-degenerate assumption. Compared with the continuous case in Hu et al. (2019, J. Differ. Equ. 266, 4106–4136) and Kong et al. (1999, J. Differ. Equ. 156, 328–354), the jump set here is involved with coefficients of the Sturm–Liouville equations. This, along with arbitrariness of the dimension, causes difficulty when dividing the jump areas. We study the singularity by partitioning and analysing the local coordinate systems, and provide a Hermitian matrix which can determine the areas’ division. To prove the asymptotic behaviour of the $n$
-th eigenvalue exhibits jump phenomena and we describe the singularity under a non-degenerate assumption. Compared with the continuous case in Hu et al. (2019, J. Differ. Equ. 266, 4106–4136) and Kong et al. (1999, J. Differ. Equ. 156, 328–354), the jump set here is involved with coefficients of the Sturm–Liouville equations. This, along with arbitrariness of the dimension, causes difficulty when dividing the jump areas. We study the singularity by partitioning and analysing the local coordinate systems, and provide a Hermitian matrix which can determine the areas’ division. To prove the asymptotic behaviour of the $n$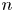 -th eigenvalue, we generalize the method developed in Zhu and Shi (2016, J. Differ. Equ. 260, 5987–6016) to any dimension. As an application, by transforming the continuous Sturm–Liouville problem of Atkinson type to a discrete one, we determine the number of eigenvalues and obtain complete characterization of jump phenomena of the $n$
-th eigenvalue, we generalize the method developed in Zhu and Shi (2016, J. Differ. Equ. 260, 5987–6016) to any dimension. As an application, by transforming the continuous Sturm–Liouville problem of Atkinson type to a discrete one, we determine the number of eigenvalues and obtain complete characterization of jump phenomena of the $n$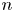 -th eigenvalue for the Atkinson type.
-th eigenvalue for the Atkinson type.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 2 , April 2023 , pp. 619 - 653
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by



