Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-03T01:05:24.130Z Has data issue: false hasContentIssue false
  • English
  • Français

Iterative bounds for the stable solutions of convex non-linear boundary value problems*

Published online by Cambridge University Press:  14 February 2012

J. W. Mooney  and
G. F. Roach
J. W. Mooney
Affiliation:
Paisley College of Technology
G. F. Roach
Affiliation:
University of Strathclyde
Get access Rights & Permissions [Opens in a new window]

Synopsis

We consider a class of convex non-linear boundary value problems of the form

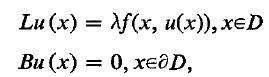
where L is a linear, uniformly elliptic, self-adjoint differential expression, f is a given non-linear function, B is a boundary differential expression of either Dirichlet or Neumann type and D is a bounded open domain with boundary ∂D. Particular problems of this class arise in the process of thermal combustion [8].

In this paper we show that stable solutions of this class can be bounded from below (above) by a monotonically increasing (decreasing) sequence of Newton (Picard) iterates. The possibility of using these schemes to construct unstable solutions is also considered.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 76 , Issue 2 , 1977 , pp. 81 - 94
Copyright
Copyright © Royal Society of Edinburgh 1977

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Keller, H. B. and Cohen, D. S.. Some positone problems suggested by nonlinear heat generation. J. Math. Mech. 16 (1967), 1361–1376.Google Scholar
2Shampine, L. F.. Some nonlinear eigenvalue problems. J. Math. Mech. 17 (1968), 1067–1072.Google Scholar
3Cohen, D. S.. Positive solutions of a class of nonlinear eigenvalue problems. J. Math. Mech. 17 (1968), 209–215.Google Scholar
4Gelfand, I. M.. Some problems in theory of quasilinear equations. Amer. Math. Soc. Transl. 29 (1963), 295–381.Google Scholar
5Fujita, H.. On the nonlinear equations . Bull. Amer. Math. Soc. 75 (1969), 132–135.CrossRefGoogle Scholar
6Sattinger, D. H.. Monotone methods in nonlinear elliptic and parabolic boundary value problems. Indiana Univ. Math. J. 21 (1972), 979–1000.CrossRefGoogle Scholar
7Joseph, D. D. and Lundgren, T. S.. Quasilinear Dirichlet problems driven by positive sources. Arch. Rational Mech. Anal. 49 (1973), 295–381.CrossRefGoogle Scholar
8Frank-Kamenetskii, D. A.. Diffusion and heat transfer in chemical kinetics (Princeton: Plenum, 1969).Google Scholar
9Collatz, L.. Functional analysis and numerical mathematics (New York: Academic, 1966).Google Scholar
10Joseph, D. D.. Nonlinear heat generation in conducting solids. Int. J. Heat and Mass Transfer 8 (1965), 281–288.CrossRefGoogle Scholar
11Courant, R. and Hilbert, D.. Methods of mathematical physics II (New York: Interscience 1962).Google Scholar
12Crandall, M. G. and Rabinowitz, P. H.. Some continuation and variational methods for positive solutions of nonlinear elliptic eigenvalue problems, in press.Google Scholar
13Krasnoselskii, M. A.. Positive solutions of operator equations (Groningen: Noordhoff, 1964).Google Scholar
14Kantorovich, L. and Akilov, G. P.. Functional analysis in normed spaces (Oxford: Pergamon, 1964).Google Scholar
15Keener, J. P. and Keller, H. B.. Positive solutions of convex nonlinear eigenvalue problems. Differential Equations 16 (1974), 103–125.CrossRefGoogle Scholar
16Bellman, R. E. and Kalaba, R.. Quasilinearization and nonlinear boundary value problems (New York: Elsevier, 1965).Google Scholar
17Kalaba, R.. On nonlinear differential equations, the maximum operation, and monotone convergence. Math. Mech. 8 (1959), 519–574.Google Scholar
18Protter, M. H. and Weinberger, H. F.. Maximum principles in differential equations (Englewood Cliffs: Prentice-Hall, 1967).Google Scholar
19Keller, H. B.. Elliptic boundary value problems suggested by nonlinear diffusion processes. Arch. Rational Mech. Anal. 35 (1969), 363–381.CrossRefGoogle Scholar
20Amann, H.. On the existence of positive solutions of nonlinear elliptic boundary value problems. Indiana Univ. Math. J. 21 (1971), 125–146.CrossRefGoogle Scholar
21Amann, H.. Supersolutions, monotone iterations, and stability. Journal Differential Equations, to appear.Google Scholar
22Amann, H.. On the number of solutions of asymptotically superlinear two point boundary value problems. Arch. Rational Mech. Anal. 55 (1974), 207–213.CrossRefGoogle Scholar
23Davies, H. T.. Introduction to nonlinear differential and integral equations (New York: Dover, 1962)Google Scholar