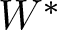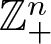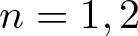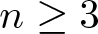1. Introduction
Consider a tuple of commuting contractions ![]() $T=(T_1,\ldots,T_n)$ on a Hilbert space H. If K is another Hilbert space that contains H and
$T=(T_1,\ldots,T_n)$ on a Hilbert space H. If K is another Hilbert space that contains H and ![]() $S=(S_1,\ldots,S_n)$ is a tuple of operators on K, we say that S is a dilation of T if, for all non-negative integers
$S=(S_1,\ldots,S_n)$ is a tuple of operators on K, we say that S is a dilation of T if, for all non-negative integers ![]() $k_1,k_2,\ldots,k_n$ and every
$k_1,k_2,\ldots,k_n$ and every ![]() $h\in H$,
$h\in H$,
 \begin{equation} T_1^{k_1}T_2^{k_2}\cdots T_n^{k_n}h=P_H S_1^{k_1}S_2^{k_2}\cdots S_n^{k_n}h, \end{equation}
\begin{equation} T_1^{k_1}T_2^{k_2}\cdots T_n^{k_n}h=P_H S_1^{k_1}S_2^{k_2}\cdots S_n^{k_n}h, \end{equation}where PH is the orthogonal projection of K onto H.
Two special cases of dilation are as follows. When H is invariant for each Si, and then, we call S an extension of T and can write (1.1) simply as
for all i, or when H is co-invariant for each Si (that is. ![]() $K\ominus H$ is invariant) and then we call S a co-extension of T. In the latter case, it is convenient to write
$K\ominus H$ is invariant) and then we call S a co-extension of T. In the latter case, it is convenient to write ![]() $\imath$ for the inclusion of H into K (an isometry) and write (1.1) by
$\imath$ for the inclusion of H into K (an isometry) and write (1.1) by
for all i. In general, instead of just ![]() $K\supseteq H$, if there is an isometry
$K\supseteq H$, if there is an isometry ![]() $\Pi: H\to K$ such that
$\Pi: H\to K$ such that
for all i, then we say S is a co-extension of T. We will mostly be interested in the case where Si commute and are isometries and refer to (1.2) in this case as isometric dilation.
It is known that if each Ti is an isometry, then T has a unitary extension ![]() $U=(U_1,\ldots, U_n)$ (so that each Ui is unitary and the Ui pairwise commute). Thus, if T has an isometric dilation, it also has a unitary dilation.
$U=(U_1,\ldots, U_n)$ (so that each Ui is unitary and the Ui pairwise commute). Thus, if T has an isometric dilation, it also has a unitary dilation.
The existence of unitary or isometric dilation is important since it enables us, in many situations, to reduce the study of a tuple T to that of a unitary or an isometric tuple, which is better understood.
For n = 1 or n = 2, it is known (see [Reference Sz.-Nagy and Foias18] and [Reference Ando2]) that isometric dilation always exists. But Parrot ([Reference Parrott12]) showed that for ![]() $n\geq 3$, one can find commuting tuples that do not have an isometric dilation.
$n\geq 3$, one can find commuting tuples that do not have an isometric dilation.
This raises the problem of finding classes of commuting tuples for which isometric dilation exists.
In 1961, Brehmer introduced a condition on a commutative tuple of contractions that ensures that the tuple has an isometric dilation. In fact, this condition is equivalent to the existence of an isometric dilation with an extra property, called regular dilation (see [Reference Ambrozie, Muller and Alpay1], [Reference Brehmer5] , or [Reference Sz.-Nagy and Foias18] for details).
In [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman7], the authors introduced the class ![]() $\mathcal{P}^n_{p,q}$ (where
$\mathcal{P}^n_{p,q}$ (where ![]() $1\leq p \lt q \leq n$) of n-commuting tuples of strict contractions that satisfy the two positivity conditions
$1\leq p \lt q \leq n$) of n-commuting tuples of strict contractions that satisfy the two positivity conditions
 \begin{equation}
\Sigma_{G\subseteq \{1,\ldots,n\}\backslash \{p\}} (-1)^{|G|} T_GT^{*}_G \geq 0 \end{equation}
\begin{equation}
\Sigma_{G\subseteq \{1,\ldots,n\}\backslash \{p\}} (-1)^{|G|} T_GT^{*}_G \geq 0 \end{equation}and
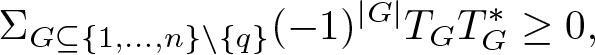 \begin{equation}\Sigma_{G\subseteq \{1,\ldots,n\}\backslash \{q\}} (-1)^{|G|} T_GT^{*}_G \geq 0, \end{equation}
\begin{equation}\Sigma_{G\subseteq \{1,\ldots,n\}\backslash \{q\}} (-1)^{|G|} T_GT^{*}_G \geq 0, \end{equation} where ![]() $T_G=T_{i_1}\cdots T_{i_{k} } $ for
$T_G=T_{i_1}\cdots T_{i_{k} } $ for ![]() $G=\{i_1,\ldots,i_k\}$. They proved that tuples in
$G=\{i_1,\ldots,i_k\}$. They proved that tuples in ![]() $\mathcal{P}^n_{p,q}$ have unitary dilations.
$\mathcal{P}^n_{p,q}$ have unitary dilations.
Another result in this direction can be found in [Reference Barik and Das3], where the class of tuples, considered by the authors for finding isometric dilation, enlarges the class considered in [Reference Brehmer5] and [Reference Grinshpan, Kaliuzhnyi-Verbovetskyi, Vinnikov and Woerdeman7].
But the result that is most relevant to us here was obtained in [Reference Barik, Das, Haria and Sarkar4]. To state it, we need the following notation. If ![]() $T=(T_1,\ldots,T_n)$ is a commuting tuple of contractions, we say that it is pure if, for every
$T=(T_1,\ldots,T_n)$ is a commuting tuple of contractions, we say that it is pure if, for every ![]() $h\in H$ and
$h\in H$ and ![]() $1\leq i \leq n$,
$1\leq i \leq n$, ![]() $T_i^{*m}h\rightarrow 0$ as
$T_i^{*m}h\rightarrow 0$ as ![]() $m\rightarrow \infty$. Also, we write
$m\rightarrow \infty$. Also, we write ![]() $\widehat{T_p}$ for the n − 1 tuple, which we get when we delete Tp from T. Finally, we say that the tuple T satisfies the Szegö positivity condition if
$\widehat{T_p}$ for the n − 1 tuple, which we get when we delete Tp from T. Finally, we say that the tuple T satisfies the Szegö positivity condition if
 \begin{equation}
\Sigma_{G\subseteq \{1,\ldots,n\}} (-1)^{|G|}T_GT_G^* \geq 0.
\end{equation}
\begin{equation}
\Sigma_{G\subseteq \{1,\ldots,n\}} (-1)^{|G|}T_GT_G^* \geq 0.
\end{equation} Note that condition (1.3) means that ![]() $\widehat{T}_p$ satisfies the Szegö condition (and a similar comment applies to condition (1.4)).
$\widehat{T}_p$ satisfies the Szegö condition (and a similar comment applies to condition (1.4)).
This allows us to define the class ![]() $\mathcal{T}_{p,q}^n$ (for
$\mathcal{T}_{p,q}^n$ (for ![]() $1\leq p \lt q\leq n$) to be
$1\leq p \lt q\leq n$) to be
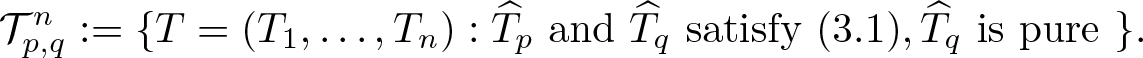 \begin{equation}
\mathcal{T}_{p,q}^n:= \{T=(T_1,\ldots,T_n) : \widehat{T}_p \ \mbox{and } \widehat{T}_q \ \mbox{satisfy } (3.1) , \widehat{T}_q \ \mbox{is pure } \}.
\end{equation}
\begin{equation}
\mathcal{T}_{p,q}^n:= \{T=(T_1,\ldots,T_n) : \widehat{T}_p \ \mbox{and } \widehat{T}_q \ \mbox{satisfy } (3.1) , \widehat{T}_q \ \mbox{is pure } \}.
\end{equation} The main result of [Reference Barik, Das, Haria and Sarkar4] is that every ![]() $T\in \mathcal{T}_{p,q}^n$ has an isometric dilation. In fact, such a dilation is explicitly constructed.
$T\in \mathcal{T}_{p,q}^n$ has an isometric dilation. In fact, such a dilation is explicitly constructed.
In this article, we study dilations of representations of product systems of ![]() $W^*$-correspondences. As we shall explain, a commuting tuple of contractions can be viewed as such a representation so that our study is a generalization of the study of dilations of such tuples.
$W^*$-correspondences. As we shall explain, a commuting tuple of contractions can be viewed as such a representation so that our study is a generalization of the study of dilations of such tuples.
Throughout the article, M will be a von Neumann algebra. We will think of M abstractly, that is, a ![]() $C^*$-algebra, which is a dual space, without a preferred representation, unless otherwise specified. Thus, we will refer to it as a
$C^*$-algebra, which is a dual space, without a preferred representation, unless otherwise specified. Thus, we will refer to it as a ![]() $W^*$-algebra.
$W^*$-algebra.
We now fix a ![]() $W^*$-algebra M. A
$W^*$-algebra M. A ![]() $W^*$-correspondence over the
$W^*$-correspondence over the ![]() $W^*$-algebra M is a Hilbert
$W^*$-algebra M is a Hilbert ![]() $W^*$-module E over M endowed with the structure of a left M-module via a normal
$W^*$-module E over M endowed with the structure of a left M-module via a normal ![]() $^*$-homomorphism
$^*$-homomorphism ![]() $\varphi_E :M \rightarrow
\mathcal{L}(E)$. An isomorphism between two correspondences is a bimodule isomorphism that preserves the inner product. Given two
$\varphi_E :M \rightarrow
\mathcal{L}(E)$. An isomorphism between two correspondences is a bimodule isomorphism that preserves the inner product. Given two ![]() $W^*$-correspondences E and F over M, one can define the (balanced) tensor product
$W^*$-correspondences E and F over M, one can define the (balanced) tensor product ![]() $E\otimes F$, and it is a
$E\otimes F$, and it is a ![]() $W^*$-correspondence with a natural left and right multiplication and the interior inner product is given, on generators, by
$W^*$-correspondence with a natural left and right multiplication and the interior inner product is given, on generators, by
for ![]() $e_i\in E$ and
$e_i\in E$ and ![]() $f_i\in F$.
$f_i\in F$.
If ![]() $M=\mathbb{C}$, then a
$M=\mathbb{C}$, then a ![]() $W^*$-correspondence over M is a Hilbert space, and the tensor product has the usual meaning. However, note that, for a general M,
$W^*$-correspondence over M is a Hilbert space, and the tensor product has the usual meaning. However, note that, for a general M, ![]() $E\otimes F$ is not always isomorphic to
$E\otimes F$ is not always isomorphic to ![]() $F\otimes E$.
$F\otimes E$.
A completely contractive representation (a c.c. representation) of E on a Hilbert space H is a pair ![]() $(\sigma,T)$, where σ is a representation of M on H and
$(\sigma,T)$, where σ is a representation of M on H and ![]() $T:E\rightarrow B(H)$ is a completely contractive linear map that is also a bimodule map (i.e.,
$T:E\rightarrow B(H)$ is a completely contractive linear map that is also a bimodule map (i.e., ![]() $T(a\cdot \xi \cdot b)=\sigma(a)T(\xi)\sigma(b)$ for
$T(a\cdot \xi \cdot b)=\sigma(a)T(\xi)\sigma(b)$ for ![]() $a,b \in M$ and
$a,b \in M$ and ![]() $\xi \in E$). The representation is said to be isometric (or Toeplitz) if
$\xi \in E$). The representation is said to be isometric (or Toeplitz) if ![]() $T(\xi)^*T(\eta)=\sigma(\langle
\xi,\eta \rangle)$ for every
$T(\xi)^*T(\eta)=\sigma(\langle
\xi,\eta \rangle)$ for every ![]() $\xi,\eta \in E$.
$\xi,\eta \in E$.
In [Reference Fowler6], Fowler studied product systems over a left-cancellative, countable, semigroup P with an identity e. A product system ![]() $\mathbb{E}$ is a family
$\mathbb{E}$ is a family ![]() $\{X_s\}_{s\in P}$ with isomorphisms
$\{X_s\}_{s\in P}$ with isomorphisms ![]() $\{\theta_{s,t}: X_s \otimes X_t \rightarrow X_{st} \}_{s,t \in P}$ such that
$\{\theta_{s,t}: X_s \otimes X_t \rightarrow X_{st} \}_{s,t \in P}$ such that ![]() $X_e=M$, the maps
$X_e=M$, the maps ![]() $\theta_{e,t}$ and
$\theta_{e,t}$ and ![]() $\theta_{s,e}$ are given by the left and right multiplications, and it satisfies the associativity condition
$\theta_{s,e}$ are given by the left and right multiplications, and it satisfies the associativity condition
In this article, we study the case where ![]() $P=\mathbb{Z}_+^n$. We write
$P=\mathbb{Z}_+^n$. We write ![]() $\textbf{e}_i=(0,0,\ldots, 1, \ldots,0)$ (with 1 in the i-th position) and for a product system
$\textbf{e}_i=(0,0,\ldots, 1, \ldots,0)$ (with 1 in the i-th position) and for a product system  $\{X_s\}_{s\in \mathbb{Z}_+^n}$, we write Ei for
$\{X_s\}_{s\in \mathbb{Z}_+^n}$, we write Ei for ![]() $X_{\textbf{e}_i}$,
$X_{\textbf{e}_i}$, ![]() $1\leq i \leq n$.
$1\leq i \leq n$.
It will be convenient to write ![]() $E_i^n$ for the n-fold tensor product
$E_i^n$ for the n-fold tensor product ![]() $E_i^{\otimes n}$ and to identify
$E_i^{\otimes n}$ and to identify ![]() $X_{\textbf{m}}$ (for
$X_{\textbf{m}}$ (for ![]() $\textbf{m} =(m_1,m_2,\ldots,m_n)\in \mathbb{Z}_+^n$) with
$\textbf{m} =(m_1,m_2,\ldots,m_n)\in \mathbb{Z}_+^n$) with ![]() $E_1^{m_1}\otimes E_2^{m_2} \otimes \cdots
\otimes E_k^{m_n}$ (where these tensor products are the balanced tensor products over M). That means, in particular, that the isomorphisms
$E_1^{m_1}\otimes E_2^{m_2} \otimes \cdots
\otimes E_k^{m_n}$ (where these tensor products are the balanced tensor products over M). That means, in particular, that the isomorphisms  $\theta_{\textbf{e}_i,\textbf{e}_j}$, for
$\theta_{\textbf{e}_i,\textbf{e}_j}$, for ![]() $i\leq j$, are identity maps. Setting
$i\leq j$, are identity maps. Setting  $t_{i,j}=\theta_{\textbf{e}_i,\textbf{e}_j}:E_i\otimes E_j \rightarrow
E_j \otimes E_i$ for
$t_{i,j}=\theta_{\textbf{e}_i,\textbf{e}_j}:E_i\otimes E_j \rightarrow
E_j \otimes E_i$ for ![]() $i\geq j$ (and
$i\geq j$ (and  $t_{i,j}=t_{j,i}^{-1}$ for i < j), one can check that the family
$t_{i,j}=t_{j,i}^{-1}$ for i < j), one can check that the family ![]() $\{t_{i,j}: 1\leq i,j \leq n\}$ satisfies
$\{t_{i,j}: 1\leq i,j \leq n\}$ satisfies
 \begin{equation}
(t_{j,i}\otimes
I_{\textbf{e}_l})(I_{\textbf{e}_j}\otimes t_{l,i})(t_{l,j}\otimes I_{\textbf{e}_i})=
(I_{\textbf{e}_i}\otimes t_{l,j})
(t_{l,i}\otimes I_{\textbf{e}_j})(I_{\textbf{e}_l}\otimes t_{j,i})
\end{equation}
\begin{equation}
(t_{j,i}\otimes
I_{\textbf{e}_l})(I_{\textbf{e}_j}\otimes t_{l,i})(t_{l,j}\otimes I_{\textbf{e}_i})=
(I_{\textbf{e}_i}\otimes t_{l,j})
(t_{l,i}\otimes I_{\textbf{e}_j})(I_{\textbf{e}_l}\otimes t_{j,i})
\end{equation} for every ![]() $1\leq i,j,l \leq n$. One can also check (but we omit the tedious computation) that, given n correspondences
$1\leq i,j,l \leq n$. One can also check (but we omit the tedious computation) that, given n correspondences ![]() $E_1,\ldots,E_n$ over the
$E_1,\ldots,E_n$ over the ![]() $W^*$-algebra M and a family
$W^*$-algebra M and a family ![]() $\{t_{i,j}:1\leq i,j \leq n\}$ such that
$\{t_{i,j}:1\leq i,j \leq n\}$ such that ![]() $t_{i,j}:E_i \otimes E_j \rightarrow E_j\otimes E_i$ is an isomorphism,
$t_{i,j}:E_i \otimes E_j \rightarrow E_j\otimes E_i$ is an isomorphism,  $t_{i,j}=t_{j,i}^{-1}$ and
$t_{i,j}=t_{j,i}^{-1}$ and ![]() $t_{i,i}$ is the identity map, it determines, in a unique way, a product system X (with
$t_{i,i}$ is the identity map, it determines, in a unique way, a product system X (with  $X_{\textbf{m}}=E_1^{m_1}\otimes \cdots \otimes E_k^{m_k}$) whose isomorphisms
$X_{\textbf{m}}=E_1^{m_1}\otimes \cdots \otimes E_k^{m_k}$) whose isomorphisms ![]() $\{\theta_{\textbf{n},\textbf{m}}\}$ satisfy
$\{\theta_{\textbf{n},\textbf{m}}\}$ satisfy  $\theta_{\textbf{e}_i,\textbf{e}_j}=id$ if
$\theta_{\textbf{e}_i,\textbf{e}_j}=id$ if ![]() $i\leq j$ and
$i\leq j$ and  $\theta_{\textbf{e}_i,\textbf{e}_j}=
t_{i,j}$ if i > j.
$\theta_{\textbf{e}_i,\textbf{e}_j}=
t_{i,j}$ if i > j.
In this article, we study the representations of such product systems (and their isometric dilations). In definition 2.7, we define a c.c. (and isometric) representation of product systems, and in example 3.5, we show that when ![]() $E_i=\mathbb{C}$ for all i and
$E_i=\mathbb{C}$ for all i and ![]() $t_{i,j}(x\otimes y)=y\otimes x$ (for
$t_{i,j}(x\otimes y)=y\otimes x$ (for ![]() $x\in E_i$ and
$x\in E_i$ and ![]() $y\in E_j$), a c.c representation of the product system is given by a tuple of commuting contractions. Similarly, an isometric representation, in this case, is given by a tuple of commuting isometries.
$y\in E_j$), a c.c representation of the product system is given by a tuple of commuting contractions. Similarly, an isometric representation, in this case, is given by a tuple of commuting isometries.
In [Reference Solel17, theorem 3.3], it is shown that under a condition that extends Brehmer’s condition to product systems, the c.c. representation has an isometric dilation.
The main result of the current article is theorem 3.20. We prove there that under conditions of pureness and Szegö positivity (as in (3.4)), the c.c. representation of the product system has an isometric dilation. In fact, this dilation is explicitly constructed.
Note that, for n = 1 or n = 2, this result is known to hold in general (no conditions are needed). For n = 1, it was proved in [Reference Muhly and Solel8], and for n = 2, in [Reference Solel16, theorem 4.4]. But, for ![]() $n\geq 3$, it does not hold in general as is known for the special case of isometric dilations of a tuple of commuting contractions.
$n\geq 3$, it does not hold in general as is known for the special case of isometric dilations of a tuple of commuting contractions.
Our main result is a generalization of the dilation result of [Reference Barik, Das, Haria and Sarkar4] . In the case where ![]() $E_i=E_j=\mathbb{C}$, our result here, theorem 3.20, reduces to the main result of [Reference Barik, Das, Haria and Sarkar4].
$E_i=E_j=\mathbb{C}$, our result here, theorem 3.20, reduces to the main result of [Reference Barik, Das, Haria and Sarkar4].
In [Reference Fowler6], Fowler showed that there is a universal ![]() $C^*$- algebra, written
$C^*$- algebra, written ![]() $\mathcal{T}_{\mathbb{E}}$, which is universal for isometric representations of the product system
$\mathcal{T}_{\mathbb{E}}$, which is universal for isometric representations of the product system ![]() $\mathbb{E}$. It follows from our theorem that every c.c. representation of
$\mathbb{E}$. It follows from our theorem that every c.c. representation of ![]() $\mathbb{E}$ on H that satisfies our conditions defines a completely positive map from
$\mathbb{E}$ on H that satisfies our conditions defines a completely positive map from ![]() $\mathcal{T}_{\mathbb{E}}$ into B(H).
$\mathcal{T}_{\mathbb{E}}$ into B(H).
We present several examples to show that our result yields also some other interesting special cases.
As we noted earlier, every isometric tuple has an extension to a unitary tuple. This is not always the case for representations of a product system even for the case n = 1 (see [Reference Muhly and Solel8, chapter 5] and [Reference Muhly and Solel10]).
Throughout the article, we use several variations of the letter ‘D’ to denote some particular types of operators and spaces. For the convenience of the readers, we are listing the variations here, mentioning the places where they have been defined in the article: DT,  $D_{\hat{T}_1}$,
$D_{\hat{T}_1}$, ![]() $D_{\hat{T}_n}$, and
$D_{\hat{T}_n}$, and  $D_{\hat{T}_{1n}}$ are operators where the first one is defined in (3.2) and the others are defined in the statement of proposition 3.6. The spaces
$D_{\hat{T}_{1n}}$ are operators where the first one is defined in (3.2) and the others are defined in the statement of proposition 3.6. The spaces  $\mathcal{D}_{\hat{T_1}}$ and
$\mathcal{D}_{\hat{T_1}}$ and ![]() $\mathcal{D}_{\hat{T_n}}$ are defined in the paragraph just above proposition 3.7.
$\mathcal{D}_{\hat{T_n}}$ are defined in the paragraph just above proposition 3.7. ![]() $\mathcal{D}_1$,
$\mathcal{D}_1$, ![]() $\mathcal{D}_2$,
$\mathcal{D}_2$, ![]() $\mathcal{D}$,
$\mathcal{D}$, ![]() $\mathcal{D}'$, and
$\mathcal{D}'$, and ![]() $\mathcal{D}_{1n}$ are some spaces that are defined in (3.10), (3.11), (3.13), (3.14), and (3.25), respectively.
$\mathcal{D}_{1n}$ are some spaces that are defined in (3.10), (3.11), (3.13), (3.14), and (3.25), respectively.
2. Preliminaries
We begin by recalling the notion of a ![]() $W^*$-correspondence.
$W^*$-correspondence.
Definition 2.1. A ![]() $W^*$-correspondence over a
$W^*$-correspondence over a ![]() $W^*$-algebra M is a Hilbert
$W^*$-algebra M is a Hilbert ![]() $W^*$-module E over M, in the sense of Paschke [Reference Paschke13], endowed with the structure of a left M-module via a normal
$W^*$-module E over M, in the sense of Paschke [Reference Paschke13], endowed with the structure of a left M-module via a normal ![]() $^*$-homomorphism
$^*$-homomorphism ![]() $\varphi_E :M \rightarrow
\mathcal{L}(E)$.
$\varphi_E :M \rightarrow
\mathcal{L}(E)$.
If E and F are ![]() $W^*$-correspondences over M, then the balanced tensor product
$W^*$-correspondences over M, then the balanced tensor product ![]() $E\otimes_M F$ is a
$E\otimes_M F$ is a ![]() $W^*$-correspondence over M. It is defined as the self-dual Hausdorff completion of the algebraic balanced tensor product with the internal inner product given by
$W^*$-correspondence over M. It is defined as the self-dual Hausdorff completion of the algebraic balanced tensor product with the internal inner product given by
for all ![]() $\xi_1,\xi_2 \in E$ and
$\xi_1,\xi_2 \in E$ and ![]() $\eta_1,\eta_2 \in F$. The left and right actions of
$\eta_1,\eta_2 \in F$. The left and right actions of ![]() $a\in M$ are defined by
$a\in M$ are defined by
for all ![]() $a,b\in M$,
$a,b\in M$, ![]() $\xi\in E$, and
$\xi\in E$, and ![]() $\eta\in F$.
$\eta\in F$.
Definition 2.2. An isomorphism of ![]() $W^*$-correspondences E and F is a surjective, bimodule map that preserves the inner products. We write
$W^*$-correspondences E and F is a surjective, bimodule map that preserves the inner products. We write ![]() $E\cong F$ if such an isomorphism exists.
$E\cong F$ if such an isomorphism exists.
If E is a ![]() $W^*$-correspondence over M and σ is a normal representation of M on a Hilbert space H, then
$W^*$-correspondence over M and σ is a normal representation of M on a Hilbert space H, then ![]() $E\otimes_{\sigma}H$ is the Hilbert space obtained as the Hausdorff completion of the algebraic tensor product with respect to
$E\otimes_{\sigma}H$ is the Hilbert space obtained as the Hausdorff completion of the algebraic tensor product with respect to ![]() $\langle \xi \otimes h, \eta \otimes k \rangle=\langle
h,\sigma(\langle \xi,\eta \rangle_E)k\rangle_H $. Given an operator
$\langle \xi \otimes h, \eta \otimes k \rangle=\langle
h,\sigma(\langle \xi,\eta \rangle_E)k\rangle_H $. Given an operator ![]() $X\in \mathcal{L}(E)$ and an operator
$X\in \mathcal{L}(E)$ and an operator ![]() $S\in \sigma(M)'$, the map
$S\in \sigma(M)'$, the map ![]() $\xi \otimes h \mapsto X\xi \otimes Sh $ defines a bounded operator
$\xi \otimes h \mapsto X\xi \otimes Sh $ defines a bounded operator ![]() $X\otimes S$ on
$X\otimes S$ on ![]() $E\otimes_{\sigma}H$. When
$E\otimes_{\sigma}H$. When ![]() $S=I_H$ and
$S=I_H$ and ![]() $X=\varphi_E(a)$ (for
$X=\varphi_E(a)$ (for ![]() $a\in M$), we get a normal representation of M on this Hilbert space. We frequently write
$a\in M$), we get a normal representation of M on this Hilbert space. We frequently write ![]() $a\otimes I_H$ for
$a\otimes I_H$ for ![]() $\varphi(a)\otimes I_H$.
$\varphi(a)\otimes I_H$.
Definition 2.3. Let E be a ![]() $W^*$-correspondence over a
$W^*$-correspondence over a ![]() $W^*$-algebra M. Then, a completely contractive covariant representation of E (or, simply, a c.c. representation of E) on a Hilbert space H is a pair
$W^*$-algebra M. Then, a completely contractive covariant representation of E (or, simply, a c.c. representation of E) on a Hilbert space H is a pair ![]() $(\sigma,T)$, where
$(\sigma,T)$, where
(i) σ is a normal
 $\ast$-representation of M in B(H).
$\ast$-representation of M in B(H).(ii) T is a linear, completely contractive map from E to B(H).
(iii) T is a bimodule map in the sense that
 $T(a\xi b)=\sigma(a)T(\xi
)\sigma(b)$,
$T(a\xi b)=\sigma(a)T(\xi
)\sigma(b)$,  $\xi\in E$, and
$\xi\in E$, and  $a,b\in M$.
$a,b\in M$.
Such a representation is said to be isometric if, for every ![]() $\xi,\eta\in E$,
$\xi,\eta\in E$, ![]() $T(\xi)^*T(\eta)=\sigma(\langle \xi,\eta
\rangle)$.
$T(\xi)^*T(\eta)=\sigma(\langle \xi,\eta
\rangle)$.
As was shown in [Reference Muhly and Solel8, lemmas 3.4–3.6], if a completely contractive covariant representation, ![]() $(\sigma,T)$, of E in B(H) is given, then it determines a contraction
$(\sigma,T)$, of E in B(H) is given, then it determines a contraction ![]() $\tilde{T}:E\otimes_{\sigma}H\rightarrow H$ defined by the formula
$\tilde{T}:E\otimes_{\sigma}H\rightarrow H$ defined by the formula ![]() $\tilde
{T}(\eta\otimes h):=T(\eta)h$,
$\tilde
{T}(\eta\otimes h):=T(\eta)h$, ![]() $\eta\otimes h\in E\otimes_{\sigma}H$. The operator
$\eta\otimes h\in E\otimes_{\sigma}H$. The operator ![]() $\tilde{T}$ satisfies
$\tilde{T}$ satisfies
In fact, we have the following lemma from [Reference Muhly and Solel9, lemma 2.16]:
Lemma 2.4. The map ![]() $(\sigma,T)\rightarrow\tilde{T}$ is a bijection between all completely contractive covariant representations
$(\sigma,T)\rightarrow\tilde{T}$ is a bijection between all completely contractive covariant representations ![]() $(\sigma,T)$ of E on the Hilbert space H and contractive operators
$(\sigma,T)$ of E on the Hilbert space H and contractive operators ![]() $\tilde{T}:E\otimes_{\sigma }H\rightarrow H$ that satisfy equation (2.3). Given σ and a contraction
$\tilde{T}:E\otimes_{\sigma }H\rightarrow H$ that satisfy equation (2.3). Given σ and a contraction ![]() $\tilde{T}$ satisfying the covariance condition (2.3), we get a completely contractive covariant representation
$\tilde{T}$ satisfying the covariance condition (2.3), we get a completely contractive covariant representation ![]() $(\sigma,T)$ of E on H by setting
$(\sigma,T)$ of E on H by setting ![]() $T(\xi)h:=\tilde{T}
(\xi\otimes h)$.
$T(\xi)h:=\tilde{T}
(\xi\otimes h)$.
Moreover, the representation ![]() $(\sigma,T)$ is an isometric representation if and only if
$(\sigma,T)$ is an isometric representation if and only if ![]() $\tilde{T}$ is an isometry.
$\tilde{T}$ is an isometry.
Remark 2.5. In addition to ![]() $\tilde{T}$, we also require the ‘generalized higher powers’ of
$\tilde{T}$, we also require the ‘generalized higher powers’ of ![]() $\tilde{T}$. These are maps
$\tilde{T}$. These are maps![]() $\;\tilde{T}^{(n)}:E^{\otimes n}\otimes
H\rightarrow H\;$defined by the equation
$\;\tilde{T}^{(n)}:E^{\otimes n}\otimes
H\rightarrow H\;$defined by the equation![]() $\;\tilde{T}^{(n)}(\xi_{1}\otimes
\ldots\otimes\xi_{n}\otimes h)=T(\xi_{1})\cdots T(\xi_{n})h$,
$\;\tilde{T}^{(n)}(\xi_{1}\otimes
\ldots\otimes\xi_{n}\otimes h)=T(\xi_{1})\cdots T(\xi_{n})h$, ![]() $\xi_{1}
\otimes\ldots\otimes\xi_{n}\otimes h\in E^{\otimes n}\otimes H$. One checks easily that
$\xi_{1}
\otimes\ldots\otimes\xi_{n}\otimes h\in E^{\otimes n}\otimes H$. One checks easily that  $\tilde{T}^{(n)}=\tilde{T}\circ
(I_E\otimes \tilde{T})\circ \cdots \circ (I_{E^{\otimes n-1}}
\otimes \tilde{T})$, n > 1.
$\tilde{T}^{(n)}=\tilde{T}\circ
(I_E\otimes \tilde{T})\circ \cdots \circ (I_{E^{\otimes n-1}}
\otimes \tilde{T})$, n > 1.
Definition 2.6. A product system over M is a family of ![]() $W^*$-correspondences
$W^*$-correspondences ![]() $\{E_1,E_2. \ldots, E_n\}$ over M together with unitary isomorphisms
$\{E_1,E_2. \ldots, E_n\}$ over M together with unitary isomorphisms ![]() $t_{i,j}: E_i \otimes E_j \rightarrow E_j\otimes E_i$ (for i > j).
$t_{i,j}: E_i \otimes E_j \rightarrow E_j\otimes E_i$ (for i > j).
In fact, this defines a product system over the semigroup  $\mathbb{Z}_{+}^N$, and it is natural to define also
$\mathbb{Z}_{+}^N$, and it is natural to define also ![]() $t_{i,i}=I_{E_i}$ and
$t_{i,i}=I_{E_i}$ and  $t_{i,j}=t_{j,i}^{-1}$ for i < j. These unitaries allow us to identify
$t_{i,j}=t_{j,i}^{-1}$ for i < j. These unitaries allow us to identify ![]() $E_i\otimes E_j$ with
$E_i\otimes E_j$ with ![]() $E_j\otimes E_i$. Similarly, we can identify
$E_j\otimes E_i$. Similarly, we can identify ![]() $E_{n_1}\otimes E_{n_2} \otimes \cdots E_{n_k}$ with every permutation of the correspondences.
$E_{n_1}\otimes E_{n_2} \otimes \cdots E_{n_k}$ with every permutation of the correspondences.
In this article, we shall suppress the unitaries ![]() $t_{i,j}$ and write
$t_{i,j}$ and write ![]() $E_i\otimes E_j=E_j\otimes E_i$. The case where the unitaries
$E_i\otimes E_j=E_j\otimes E_i$. The case where the unitaries ![]() $t_{i,j}$’s are involved in the commutation relations can be computed in a similar way, and the same results hold.
$t_{i,j}$’s are involved in the commutation relations can be computed in a similar way, and the same results hold.
Definition 2.7. A c.c. (completely contractive) representation of a product system ![]() $(M,E_1,\ldots,E_n )$ is a tuple
$(M,E_1,\ldots,E_n )$ is a tuple ![]() $(\sigma, T_1,T_2,\ldots,T_n)$ where for each i,
$(\sigma, T_1,T_2,\ldots,T_n)$ where for each i, ![]() $(\sigma, T_i)$ is a representation of Ei on H (and, thus,
$(\sigma, T_i)$ is a representation of Ei on H (and, thus, ![]() $\tilde{T}_i$ is a contraction) such that Ti commutes with Tj, or more precisely,
$\tilde{T}_i$ is a contraction) such that Ti commutes with Tj, or more precisely,
 \begin{equation} \tilde{T_i}(I_{E_i}\otimes \tilde{T_j})=\tilde{T_j}(I_{E_j}\otimes \tilde{T_i})(t_{i,j}\otimes I_H)
\end{equation}
\begin{equation} \tilde{T_i}(I_{E_i}\otimes \tilde{T_j})=\tilde{T_j}(I_{E_j}\otimes \tilde{T_i})(t_{i,j}\otimes I_H)
\end{equation} for every ![]() $i,j$. If each
$i,j$. If each ![]() $(\sigma, T_i)$ is an isometric representation of Ei (equivalently, if each
$(\sigma, T_i)$ is an isometric representation of Ei (equivalently, if each ![]() $\tilde{T_i}$ is an isometry), we say that the representation (of the product system) is an isometric representation.
$\tilde{T_i}$ is an isometry), we say that the representation (of the product system) is an isometric representation.
Suppressing ![]() $t_{i,j}$, we simply write
$t_{i,j}$, we simply write
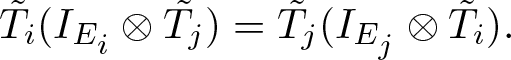 \begin{equation*} \tilde{T_i}(I_{E_i}\otimes \tilde{T_j})=\tilde{T_j}(I_{E_j}\otimes \tilde{T_i}).\end{equation*}
\begin{equation*} \tilde{T_i}(I_{E_i}\otimes \tilde{T_j})=\tilde{T_j}(I_{E_j}\otimes \tilde{T_i}).\end{equation*}Definition 2.8. We say that an isometric representation ![]() $(\sigma, V_1,V_2,\ldots,V_n)$ of the product system
$(\sigma, V_1,V_2,\ldots,V_n)$ of the product system ![]() $(M,E_1,\ldots,E_n )$ on the Hilbert space K is a dilation of the representation
$(M,E_1,\ldots,E_n )$ on the Hilbert space K is a dilation of the representation ![]() $(\sigma, T_1,T_2,\ldots,T_n)$ (on H) if there is an isometry
$(\sigma, T_1,T_2,\ldots,T_n)$ (on H) if there is an isometry ![]() $\Pi:H\rightarrow K$ such that
$\Pi:H\rightarrow K$ such that
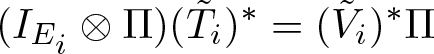 \begin{equation*} (I_{E_i} \otimes \Pi)(\tilde{T}_i)^*=(\tilde{V}_i)^* \Pi \end{equation*}
\begin{equation*} (I_{E_i} \otimes \Pi)(\tilde{T}_i)^*=(\tilde{V}_i)^* \Pi \end{equation*}for all i.
We shall use the following notation. For a subset ![]() $G=\{n_1,n_2,\ldots,n_k\}\subseteq \{1,2,\ldots,n\} $, we write EG or
$G=\{n_1,n_2,\ldots,n_k\}\subseteq \{1,2,\ldots,n\} $, we write EG or ![]() $E_{n_1,n_2,\ldots.n_k}$ for
$E_{n_1,n_2,\ldots.n_k}$ for ![]() $E_{n_1}\otimes E_{n_2} \otimes \cdots \otimes E_{n_k}$. It will also be convenient to write
$E_{n_1}\otimes E_{n_2} \otimes \cdots \otimes E_{n_k}$. It will also be convenient to write ![]() $I_1, I_n, I_{1n}$ for
$I_1, I_n, I_{1n}$ for ![]() $I_{E_1}, I_{E_n}, I_{E_1\otimes E_n}$, respectively.
$I_{E_1}, I_{E_n}, I_{E_1\otimes E_n}$, respectively.
Also, given a representation ![]() $(\sigma, T_1,T_2,\ldots,T_n)$ of the product system, and
$(\sigma, T_1,T_2,\ldots,T_n)$ of the product system, and ![]() $G\subseteq \{1,2,\ldots,n\} $ as above, we write
$G\subseteq \{1,2,\ldots,n\} $ as above, we write
 \begin{equation} \tilde{T}_G = \tilde{T}_{n_1} (I_{n_1} \otimes \tilde{T}_{n_2}) \cdots
(I_{G - \{n_k\}} \otimes \tilde{T}_{n_k})
: E_{n_1} \otimes \cdots \otimes E_{n_k} \otimes H =E_G\otimes H \to H.\end{equation}
\begin{equation} \tilde{T}_G = \tilde{T}_{n_1} (I_{n_1} \otimes \tilde{T}_{n_2}) \cdots
(I_{G - \{n_k\}} \otimes \tilde{T}_{n_k})
: E_{n_1} \otimes \cdots \otimes E_{n_k} \otimes H =E_G\otimes H \to H.\end{equation} Also, we write, for ![]() $1\leq k$,
$1\leq k$,
 \begin{equation*} \tilde{T}_G^{(k)}= \tilde{T}_G(I_{E_G}\otimes \tilde{T}_G)\cdots (I_{E_G^{\otimes {k-1}}}\otimes \tilde{T}_G )\end{equation*}
\begin{equation*} \tilde{T}_G^{(k)}= \tilde{T}_G(I_{E_G}\otimes \tilde{T}_G)\cdots (I_{E_G^{\otimes {k-1}}}\otimes \tilde{T}_G )\end{equation*}and
 \begin{equation*}
\big(\tilde{T}_G\big)^{*(k)}=\Big(\tilde{T}_G^{(k)}\Big)^*.
\end{equation*}
\begin{equation*}
\big(\tilde{T}_G\big)^{*(k)}=\Big(\tilde{T}_G^{(k)}\Big)^*.
\end{equation*} Given a product system ![]() $(M,E_1,\ldots,E_n)$ and
$(M,E_1,\ldots,E_n)$ and ![]() $\alpha\in \mathbb{Z}_+^n$, we write
$\alpha\in \mathbb{Z}_+^n$, we write  $E^{\alpha}:=E_1^{\otimes \alpha_1}\otimes E_2^{\otimes \alpha_2}\otimes\cdots \otimes E_n^{\otimes \alpha_n}$ (with
$E^{\alpha}:=E_1^{\otimes \alpha_1}\otimes E_2^{\otimes \alpha_2}\otimes\cdots \otimes E_n^{\otimes \alpha_n}$ (with ![]() $E^0:=M$) and form the associated Fock correspondence
$E^0:=M$) and form the associated Fock correspondence
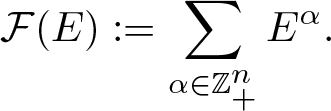 \begin{equation}
\mathcal{F}(E):=\sum _{\alpha\in \mathbb{Z}_+^n} E^{\alpha}.
\end{equation}
\begin{equation}
\mathcal{F}(E):=\sum _{\alpha\in \mathbb{Z}_+^n} E^{\alpha}.
\end{equation} In the following, we fix a ![]() $W^*$-algebra M, a product system
$W^*$-algebra M, a product system ![]() $(M,E_1,\ldots,E_n)$ over
$(M,E_1,\ldots,E_n)$ over ![]() $\mathbb{N}^n$ and a representation
$\mathbb{N}^n$ and a representation ![]() $(\sigma,T_1,\ldots,T_n)$ of the product system over H.
$(\sigma,T_1,\ldots,T_n)$ of the product system over H.
We write NRep(M) for the set of normal representations of M. For normal representations ![]() $\rho_1, \rho_2$ of M, we write
$\rho_1, \rho_2$ of M, we write ![]() $\rho_1\precsim \rho_2$ if ρ 1 is equivalent to a subrepresentation of ρ 2 and
$\rho_1\precsim \rho_2$ if ρ 1 is equivalent to a subrepresentation of ρ 2 and ![]() $\rho_1 \simeq \rho_2$ if they are equivalent. It will be convenient to write
$\rho_1 \simeq \rho_2$ if they are equivalent. It will be convenient to write ![]() $G_1\precsim G_2$ if Gi is the representation space of some normal representation of M, say ρi and
$G_1\precsim G_2$ if Gi is the representation space of some normal representation of M, say ρi and ![]() $\rho_1 \precsim \rho_2$.
$\rho_1 \precsim \rho_2$.
In [Reference Rieffel15], Rieffel defined the notion of a generator for NRep(M) (based on a similar notion in pure algebra). In [Reference Rieffel15, proposition 1.1], he showed that a normal representation ρ is a generator if and only if every representation ![]() $\pi\in NRep(M)$ is a direct sum of copies of subrepresentations of ρ. In [Reference Rieffel15, proposition 1.3], he proved that ρ is a generator if and only if it is faithful.
$\pi\in NRep(M)$ is a direct sum of copies of subrepresentations of ρ. In [Reference Rieffel15, proposition 1.3], he proved that ρ is a generator if and only if it is faithful.
As in [Reference Muhly and Solel11, definition 4.1], we say that a generator is an infinite generator if it is an infinite multiple of a generator for NRep(M), that is, it is an infinite multiple of a faithful normal representation of M. We can conclude that every infinite generator ρ has the property that every normal representation of M is equivalent to a subrepresentation of ρ. We also note that every infinite generator is unique up to equivalence.
We shall now fix an infinite generator ![]() $\rho_{\infty}$ and write
$\rho_{\infty}$ and write ![]() $H_{\infty} $ for its representation space.
$H_{\infty} $ for its representation space.
The following lemma will be useful. The proof is straightforward and will be omitted.
Lemma 2.9. Suppose E is a faithful ![]() $W^*$-correspondence over M (that is, φE is a faithful map) and ρ is a faithful representation of M on H. Then, the representation
$W^*$-correspondence over M (that is, φE is a faithful map) and ρ is a faithful representation of M on H. Then, the representation ![]() $\varphi_E(\cdot)\otimes I_H$ is a faithful representation of M on
$\varphi_E(\cdot)\otimes I_H$ is a faithful representation of M on ![]() $E\otimes_{\rho}H$.
$E\otimes_{\rho}H$.
3. Representations of product systems
We will assume that ![]() $E_1,\ldots, E_n$ are faithful
$E_1,\ldots, E_n$ are faithful ![]() $W^*$-correspondences over a
$W^*$-correspondences over a ![]() $W^*$-algebra M. It follows from lemma 2.9 that, for
$W^*$-algebra M. It follows from lemma 2.9 that, for ![]() $i=1,\ldots,n$, the representation
$i=1,\ldots,n$, the representation ![]() $\varphi_i(\cdot)\otimes_{\rho_{\infty}}I_{H_{\infty}}$ is also an infinite generator.
$\varphi_i(\cdot)\otimes_{\rho_{\infty}}I_{H_{\infty}}$ is also an infinite generator.
Recall, for each ![]() $i=1,\ldots,n$,
$i=1,\ldots,n$,
is defined by ![]() $\tilde{T_i}(\xi_i\otimes h)=T_i(\xi_i)h$ for
$\tilde{T_i}(\xi_i\otimes h)=T_i(\xi_i)h$ for ![]() $\xi_i\in E_i$ and
$\xi_i\in E_i$ and ![]() $h\in H$. Recall that for any
$h\in H$. Recall that for any ![]() $G = \{n_1,\ldots,n_k\} \subseteq \{1,\ldots,n\}$, the operator
$G = \{n_1,\ldots,n_k\} \subseteq \{1,\ldots,n\}$, the operator ![]() $\tilde{T}_G$ is defined as in (2.5).
$\tilde{T}_G$ is defined as in (2.5).
We say, the representation ![]() $(\sigma,T_1,\ldots,T_n)$ satisfies Szegö positivity if the tuple
$(\sigma,T_1,\ldots,T_n)$ satisfies Szegö positivity if the tuple ![]() $\tilde{T}= (\tilde{T}_1,\ldots,\tilde{T}_n)$ is Szegö positive, that is,
$\tilde{T}= (\tilde{T}_1,\ldots,\tilde{T}_n)$ is Szegö positive, that is,
 \begin{equation}
\mathbb{S}_n^{-1}\big(\tilde{T},(\tilde{T})^*\big) := \sum_{G \subset \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}_G \big(\tilde{T}_G\big)^*\geq 0.
\end{equation}
\begin{equation}
\mathbb{S}_n^{-1}\big(\tilde{T},(\tilde{T})^*\big) := \sum_{G \subset \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}_G \big(\tilde{T}_G\big)^*\geq 0.
\end{equation}If this holds, we write
 \begin{equation} D_T^2=\mathbb{S}_n^{-1}\big(\tilde{T},(\tilde{T})^*\big).\end{equation}
\begin{equation} D_T^2=\mathbb{S}_n^{-1}\big(\tilde{T},(\tilde{T})^*\big).\end{equation}Proposition 3.1. For a c.c. representation ![]() $(\sigma, T_1,\ldots,T_n)$ satisfying Szegö positivity, the map
$(\sigma, T_1,\ldots,T_n)$ satisfying Szegö positivity, the map ![]() $\Pi: H \to \mathcal{F}(E) \otimes H$ defined by
$\Pi: H \to \mathcal{F}(E) \otimes H$ defined by
 \begin{equation*} \Pi h = \bigoplus_{\alpha \in \mathbb Z_+^n} (I_{E^{\alpha}} \otimes D_T) (\tilde{T})^{*(\alpha)}h\end{equation*}
\begin{equation*} \Pi h = \bigoplus_{\alpha \in \mathbb Z_+^n} (I_{E^{\alpha}} \otimes D_T) (\tilde{T})^{*(\alpha)}h\end{equation*}satisfies
 \begin{equation} \|\Pi h\|^2 = \|h\|^2 + \lim_{k \to \infty} \Big\langle \sum_{\emptyset \neq G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}_G^{(k)}
\big(\tilde{T}_G\big)^{*(k)} h, h \Big \rangle,\end{equation}
\begin{equation} \|\Pi h\|^2 = \|h\|^2 + \lim_{k \to \infty} \Big\langle \sum_{\emptyset \neq G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}_G^{(k)}
\big(\tilde{T}_G\big)^{*(k)} h, h \Big \rangle,\end{equation} where ![]() $k\in\mathbb{Z}_+$.
$k\in\mathbb{Z}_+$.
Proof. Using the fact that for each ![]() $i,j \in \{1,\ldots,n\}$,
$i,j \in \{1,\ldots,n\}$,  $\tilde{T}_i (I_{E_i} \otimes \tilde{T}_j) = \tilde{T}_j (I_{E_j} \otimes \tilde{T}_i)$, we have
$\tilde{T}_i (I_{E_i} \otimes \tilde{T}_j) = \tilde{T}_j (I_{E_j} \otimes \tilde{T}_i)$, we have
 \begin{align*}
&\sum_{\alpha = (\alpha_1,\ldots, \alpha_n) \in \mathbb Z_+^n } \langle \tilde{T}^{(\alpha)}(I_{E^{\alpha}} \otimes D^{2}_T) (\tilde{T})^{*(\alpha)} h, h \rangle \\
& \quad = \lim_{k \to \infty} \sum_{\text{max} \alpha_j \leq k-1} \langle \tilde{T}^{(\alpha)} (I_{E^{\alpha}} \otimes D^{2}_T) (\tilde{T})^{*(\alpha)} h,h \rangle \\
& \quad = \lim_{k \to \infty} \sum_{\text{max} \alpha_j \leq k-1} \langle \tilde{T}^{(\alpha)} (I_{E^{\alpha}} \otimes \mathbb{S}_n^{-1}(\tilde{T}, (\tilde{T})^*) )(\tilde{T})^{*(\alpha)} h,h \rangle \\
& \quad = \lim_{k \to \infty} \sum_{\text{max} \alpha_j \leq k-1} \Big\langle \tilde{T}^{(\alpha)} \Big(I_{E^{\alpha}} \otimes \sum_{G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) (\tilde{T})^{*(\alpha)} h,h \Big\rangle \\
& \quad = \lim_{k \to \infty} \sum_{\text{max} \beta_j \leq k} \Big\langle \tilde{T}^{(\beta)} (\tilde{T})^{*(\beta)} \sum_{\alpha \leq \beta,\, \text{max} (\beta_j - \alpha_j)\leq 1,\, \text{max}\alpha_j \leq k-1} (-1)^{|\beta| - |\alpha|} h, h \Big\rangle.
\end{align*}
\begin{align*}
&\sum_{\alpha = (\alpha_1,\ldots, \alpha_n) \in \mathbb Z_+^n } \langle \tilde{T}^{(\alpha)}(I_{E^{\alpha}} \otimes D^{2}_T) (\tilde{T})^{*(\alpha)} h, h \rangle \\
& \quad = \lim_{k \to \infty} \sum_{\text{max} \alpha_j \leq k-1} \langle \tilde{T}^{(\alpha)} (I_{E^{\alpha}} \otimes D^{2}_T) (\tilde{T})^{*(\alpha)} h,h \rangle \\
& \quad = \lim_{k \to \infty} \sum_{\text{max} \alpha_j \leq k-1} \langle \tilde{T}^{(\alpha)} (I_{E^{\alpha}} \otimes \mathbb{S}_n^{-1}(\tilde{T}, (\tilde{T})^*) )(\tilde{T})^{*(\alpha)} h,h \rangle \\
& \quad = \lim_{k \to \infty} \sum_{\text{max} \alpha_j \leq k-1} \Big\langle \tilde{T}^{(\alpha)} \Big(I_{E^{\alpha}} \otimes \sum_{G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) (\tilde{T})^{*(\alpha)} h,h \Big\rangle \\
& \quad = \lim_{k \to \infty} \sum_{\text{max} \beta_j \leq k} \Big\langle \tilde{T}^{(\beta)} (\tilde{T})^{*(\beta)} \sum_{\alpha \leq \beta,\, \text{max} (\beta_j - \alpha_j)\leq 1,\, \text{max}\alpha_j \leq k-1} (-1)^{|\beta| - |\alpha|} h, h \Big\rangle.
\end{align*} Note that, for a fixed β with ![]() $\text{max} \beta_j \leq k$,
$\text{max} \beta_j \leq k$,
 \begin{equation*}
\sum_{\alpha \leq \beta,\, \text{max}(\beta_j - \alpha_j)\leq 1,\, \text{max} \alpha_j \leq k-1} (-1)^{|\beta| - |\alpha|} = 0 \end{equation*}
\begin{equation*}
\sum_{\alpha \leq \beta,\, \text{max}(\beta_j - \alpha_j)\leq 1,\, \text{max} \alpha_j \leq k-1} (-1)^{|\beta| - |\alpha|} = 0 \end{equation*} unless ![]() $\beta = (\beta_1,\ldots, \beta_n) \in \{0,k\}^n$. If
$\beta = (\beta_1,\ldots, \beta_n) \in \{0,k\}^n$. If ![]() $\beta = (\beta_1,\ldots, \beta_n) \in \{0,k\}^n$, then it is equal to
$\beta = (\beta_1,\ldots, \beta_n) \in \{0,k\}^n$, then it is equal to ![]() $(-1)^{|\text{supp} \beta|}$, where
$(-1)^{|\text{supp} \beta|}$, where ![]() $|\text{supp} \beta|$ means the number of non-zero βj’s in
$|\text{supp} \beta|$ means the number of non-zero βj’s in ![]() $\beta = (\beta_1,\ldots, \beta_n)$. Therefore, for every
$\beta = (\beta_1,\ldots, \beta_n)$. Therefore, for every ![]() $h \in H$,
$h \in H$,
 \begin{align*}
\|\Pi h\|^2 &= \lim_{k \to \infty} \Big\langle \sum_{G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}^{(k)}_G
\big(\tilde{T}_G\big)^{*(k)} h, h \Big\rangle \\
& = \|h\|^2 + \lim_{k \to \infty} \Big\langle \sum_{\emptyset \neq G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}^{(k)}_G
\big(\tilde{T}_G\big)^{*(k)} h, h \Big \rangle.
\end{align*}
\begin{align*}
\|\Pi h\|^2 &= \lim_{k \to \infty} \Big\langle \sum_{G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}^{(k)}_G
\big(\tilde{T}_G\big)^{*(k)} h, h \Big\rangle \\
& = \|h\|^2 + \lim_{k \to \infty} \Big\langle \sum_{\emptyset \neq G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}^{(k)}_G
\big(\tilde{T}_G\big)^{*(k)} h, h \Big \rangle.
\end{align*} A c.c. representation ![]() $(\sigma, T_1,\ldots, T_n)$ is said to be pure if
$(\sigma, T_1,\ldots, T_n)$ is said to be pure if ![]() $(\sigma, T_i)$ is pure for each
$(\sigma, T_i)$ is pure for each ![]() $i=1,\ldots, n$, that is,
$i=1,\ldots, n$, that is,  $\tilde{T}_i^{(k)}(\tilde{T}_i)^{*(k)}\to 0$ in the weak operator topology (WOT) as
$\tilde{T}_i^{(k)}(\tilde{T}_i)^{*(k)}\to 0$ in the weak operator topology (WOT) as ![]() $k\to\infty$.
$k\to\infty$.
Corollary 3.2. Let ![]() $(\sigma, T_1,\ldots, T_n)$ be a pure c.c. representation that satisfies Szegö positivity. Then, the map defined in proposition 3.1 is an isometry.
$(\sigma, T_1,\ldots, T_n)$ be a pure c.c. representation that satisfies Szegö positivity. Then, the map defined in proposition 3.1 is an isometry.
Proof. Since ![]() $(\sigma, T_1,\ldots, T_n)$ is pure,
$(\sigma, T_1,\ldots, T_n)$ is pure,
 \begin{equation*}
\lim_{k \to \infty} \Big\langle \sum_{\emptyset \neq G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}^{(k)}_G
\big(\tilde{T}_G\big)^{*(k)} h, h \Big \rangle=0.
\end{equation*}
\begin{equation*}
\lim_{k \to \infty} \Big\langle \sum_{\emptyset \neq G \subseteq \{1,\ldots,n\}} (-1)^{|G|} \tilde{T}^{(k)}_G
\big(\tilde{T}_G\big)^{*(k)} h, h \Big \rangle=0.
\end{equation*}So it follows from (3.3) that Π is an isometry.
We denote ![]() $\hat{T}_1:=(\sigma,T_2,\ldots,T_n)$ and
$\hat{T}_1:=(\sigma,T_2,\ldots,T_n)$ and  $\hat{T}_n:=(\sigma,T_1,\ldots,T_{n-1})$, and with the help of them, we define a class of c.c. representations namely
$\hat{T}_n:=(\sigma,T_1,\ldots,T_{n-1})$, and with the help of them, we define a class of c.c. representations namely ![]() $\mathcal{T}_{1,n}^n(\sigma, M, E_1,\ldots, E_n, H)$ in the following way:
$\mathcal{T}_{1,n}^n(\sigma, M, E_1,\ldots, E_n, H)$ in the following way:
 \begin{equation}
\mathcal{T}_{1,n}^n(\sigma, M, E_1,\ldots,E_n , H):=\{(\sigma, T_1,\ldots,T_n): \hat{T}_1,\hat{T}_n \ \text{satisfy Szeg\"o positivity and }\hat{T}_n \ \text{is pure}\}.
\end{equation}
\begin{equation}
\mathcal{T}_{1,n}^n(\sigma, M, E_1,\ldots,E_n , H):=\{(\sigma, T_1,\ldots,T_n): \hat{T}_1,\hat{T}_n \ \text{satisfy Szeg\"o positivity and }\hat{T}_n \ \text{is pure}\}.
\end{equation}Example 3.3. Let ![]() $M=\mathbb{C}$ and
$M=\mathbb{C}$ and ![]() $E_i=\mathbb{C}^d$ (
$E_i=\mathbb{C}^d$ (![]() $i=1,\ldots,n$). Let
$i=1,\ldots,n$). Let ![]() $T_i:\mathbb{C}^d\to\mathcal{B}(H)$ be written as
$T_i:\mathbb{C}^d\to\mathcal{B}(H)$ be written as ![]() $T_i=(T_{i,1},\ldots,T_{i,d})$, where
$T_i=(T_{i,1},\ldots,T_{i,d})$, where ![]() $T_{i,k}=T_i(e_k)$ (
$T_{i,k}=T_i(e_k)$ (![]() $\{e_k\} $ is the standard basis of
$\{e_k\} $ is the standard basis of ![]() $\mathbb{C}^d$). Then, for each
$\mathbb{C}^d$). Then, for each ![]() $i=1,\ldots,n$,
$i=1,\ldots,n$, ![]() $\tilde{T}_i: \mathbb{C}^d\otimes H\to H$ is given by
$\tilde{T}_i: \mathbb{C}^d\otimes H\to H$ is given by
 \begin{equation*}
\tilde{T}_i(\lambda\otimes h)=T_i(\lambda)h=(T_{i,1},\ldots,T_{i,d})\begin{bmatrix}\lambda_1\\\vdots\\\lambda_d\end{bmatrix}h=\sum_{j=1}^d\lambda_jT_i(e_j)h=\sum_{j=1}^d\lambda_jT_{i,j}h.
\end{equation*}
\begin{equation*}
\tilde{T}_i(\lambda\otimes h)=T_i(\lambda)h=(T_{i,1},\ldots,T_{i,d})\begin{bmatrix}\lambda_1\\\vdots\\\lambda_d\end{bmatrix}h=\sum_{j=1}^d\lambda_jT_i(e_j)h=\sum_{j=1}^d\lambda_jT_{i,j}h.
\end{equation*} To make it into a product system, we need to fix an isomorphism ![]() $t_{i,j}:E_i\otimes E_j \rightarrow E_j\otimes E_i$. For simplicity, we assume that
$t_{i,j}:E_i\otimes E_j \rightarrow E_j\otimes E_i$. For simplicity, we assume that
for i ≠ j, ![]() $e\in E_i=\mathbb{C}^d$, and
$e\in E_i=\mathbb{C}^d$, and ![]() $f\in E_j=\mathbb{C}^d$ (but see the remark below).
$f\in E_j=\mathbb{C}^d$ (but see the remark below).
For i ≠ j, ![]() $h\in H$,
$h\in H$, ![]() $e_k\in E_i$, and
$e_k\in E_i$, and ![]() $e_l\in E_j$, we apply equation (2.4) to get
$e_l\in E_j$, we apply equation (2.4) to get
 \begin{equation*}T_i(e_k)T_j(e_l)h=\tilde{T_i}(I_{E_i}\otimes \tilde{T_j})(e_k\otimes e_l \otimes h)=\tilde{T_j}(I_{E_j}\otimes \tilde{T_i})(t_{i,j}\otimes I_H)(e_k\otimes e_l\otimes h)=\end{equation*}
\begin{equation*}T_i(e_k)T_j(e_l)h=\tilde{T_i}(I_{E_i}\otimes \tilde{T_j})(e_k\otimes e_l \otimes h)=\tilde{T_j}(I_{E_j}\otimes \tilde{T_i})(t_{i,j}\otimes I_H)(e_k\otimes e_l\otimes h)=\end{equation*} \begin{equation*}\tilde{T_j}(I_{E_j}\otimes \tilde{T_i})(e_l\otimes e_k \otimes h)=T_j(e_l)T_i(e_k)h.\end{equation*}
\begin{equation*}\tilde{T_j}(I_{E_j}\otimes \tilde{T_i})(e_l\otimes e_k \otimes h)=T_j(e_l)T_i(e_k)h.\end{equation*}Thus, we require that
for i ≠ j and ![]() $1\leq k,l \leq d$.
$1\leq k,l \leq d$.
Also,  $\tilde{T}_i^{(2)}: \mathbb{C}^d\otimes\mathbb{C}^d\otimes H\to H$ is given by
$\tilde{T}_i^{(2)}: \mathbb{C}^d\otimes\mathbb{C}^d\otimes H\to H$ is given by
 \begin{equation*}
\tilde{T}_i^{(2)}\lambda\otimes\mu\otimes h)=\tilde{T}_i(\lambda\otimes\sum_{k=1}^d\mu_kT_{i,k}h )=\sum_{j,k=1}^d\lambda_j\mu_kT_{i,j}T_{i,k}h.
\end{equation*}
\begin{equation*}
\tilde{T}_i^{(2)}\lambda\otimes\mu\otimes h)=\tilde{T}_i(\lambda\otimes\sum_{k=1}^d\mu_kT_{i,k}h )=\sum_{j,k=1}^d\lambda_j\mu_kT_{i,j}T_{i,k}h.
\end{equation*} Identifying ![]() $\mathbb{C}^d\otimes\mathbb{C}^d$ with
$\mathbb{C}^d\otimes\mathbb{C}^d$ with ![]() $\mathbb{C}^{d^2}$ and
$\mathbb{C}^{d^2}$ and ![]() $\lambda\otimes\mu$ with the column
$\lambda\otimes\mu$ with the column ![]() $(\lambda_j\mu_k)_{j,k}$, we can write
$(\lambda_j\mu_k)_{j,k}$, we can write  $\tilde{T}_i^{(2)}$ as a row
$\tilde{T}_i^{(2)}$ as a row ![]() $(T_{i,j}T_{i,k})_{j,k}$. Similarly, for any
$(T_{i,j}T_{i,k})_{j,k}$. Similarly, for any ![]() $m\in\mathbb{N}$,
$m\in\mathbb{N}$,  $T_i^{(m)}$ can be written as the row
$T_i^{(m)}$ can be written as the row ![]() $(T_{i,j_1}\cdots T_{i,j_m})_{1\leq j_1,\ldots,j_m\leq d}$. Therefore,
$(T_{i,j_1}\cdots T_{i,j_m})_{1\leq j_1,\ldots,j_m\leq d}$. Therefore,
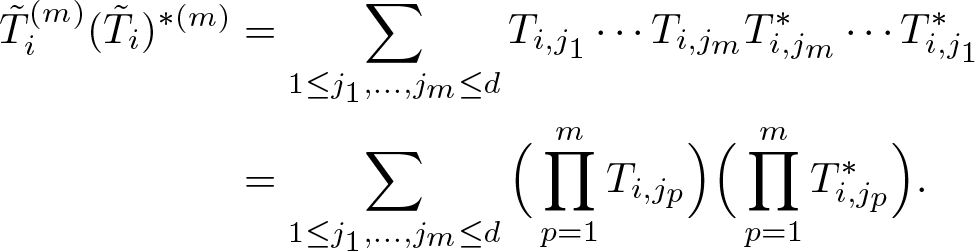 \begin{align}
\tilde{T}_i^{(m)}(\tilde{T}_i)^{*(m)}& =\sum_{1\leq j_1,\ldots,j_m\leq d}T_{i,j_1}\cdots T_{i,j_m}T_{i,j_m}^*\cdots T_{i,j_1}^*\nonumber\\
& =\sum_{1\leq j_1,\ldots,j_m\leq d}\Big(\prod_{p=1}^m T_{i,j_p}\Big)\Big(\prod_{p=1}^m T_{i,j_p}^*\Big).
\end{align}
\begin{align}
\tilde{T}_i^{(m)}(\tilde{T}_i)^{*(m)}& =\sum_{1\leq j_1,\ldots,j_m\leq d}T_{i,j_1}\cdots T_{i,j_m}T_{i,j_m}^*\cdots T_{i,j_1}^*\nonumber\\
& =\sum_{1\leq j_1,\ldots,j_m\leq d}\Big(\prod_{p=1}^m T_{i,j_p}\Big)\Big(\prod_{p=1}^m T_{i,j_p}^*\Big).
\end{align} In a similar fashion, for each ![]() $G=\{i_1,\ldots,i_k\}\subset\{1,\ldots,n\}$,
$G=\{i_1,\ldots,i_k\}\subset\{1,\ldots,n\}$,
 \begin{equation*}
\tilde{T}_G\big(\tilde{T}_G\big)^*=\sum_{1\leq j_1,\ldots,j_k\leq d}\Big(\prod_{p=1}^k T_{i_p,j_p}\Big)\Big(\prod_{p=1}^k T_{i_p,j_p}^*\Big).
\end{equation*}
\begin{equation*}
\tilde{T}_G\big(\tilde{T}_G\big)^*=\sum_{1\leq j_1,\ldots,j_k\leq d}\Big(\prod_{p=1}^k T_{i_p,j_p}\Big)\Big(\prod_{p=1}^k T_{i_p,j_p}^*\Big).
\end{equation*}Note that, due to the commutation relation (3.5), the last expression is independent of the order chosen on G. Therefore,
 \begin{align}
& \sum_{G=\{i_1,\ldots,i_k\}\subset\{1,\ldots,n\}}(-1)^{|G|}\tilde{T}_G\big(\tilde{T}_G\big)^*\nonumber\\
& \quad =\sum_{G=\{i_1,\ldots,i_k\}\subset\{1,\ldots,n\}}(-1)^{|G|}\sum_{1\leq j_1,\ldots,j_k\leq d}\Big(\prod_{p=1}^k T_{i_p,j_p}\Big)\Big(\prod_{p=1}^k T_{i_p,j_p}^*\Big).
\end{align}
\begin{align}
& \sum_{G=\{i_1,\ldots,i_k\}\subset\{1,\ldots,n\}}(-1)^{|G|}\tilde{T}_G\big(\tilde{T}_G\big)^*\nonumber\\
& \quad =\sum_{G=\{i_1,\ldots,i_k\}\subset\{1,\ldots,n\}}(-1)^{|G|}\sum_{1\leq j_1,\ldots,j_k\leq d}\Big(\prod_{p=1}^k T_{i_p,j_p}\Big)\Big(\prod_{p=1}^k T_{i_p,j_p}^*\Big).
\end{align} If the expression of the right-hand side of (3.6) tends to 0 in WOT as ![]() $m\to\infty$, then Ti is pure, and if it happens for each
$m\to\infty$, then Ti is pure, and if it happens for each ![]() $i=1,\ldots,n$, then the c.c. representation
$i=1,\ldots,n$, then the c.c. representation ![]() $(\sigma,T_1,\ldots,T_n)$ is pure. On the other hand, if the expression on the right-hand side of (3.7) is a positive operator, then the representation
$(\sigma,T_1,\ldots,T_n)$ is pure. On the other hand, if the expression on the right-hand side of (3.7) is a positive operator, then the representation ![]() $(\sigma,T_1,\ldots,T_n)$ is Szegö positive. If the above two hold together, then the representation
$(\sigma,T_1,\ldots,T_n)$ is Szegö positive. If the above two hold together, then the representation ![]() $(\sigma,T_1,\ldots,T_n)$ lies in the class
$(\sigma,T_1,\ldots,T_n)$ lies in the class  $\mathcal{T}_{1,n}^n(\sigma, \mathbb{C},\mathbb{C}^d,\ldots,\mathbb{C}^d , H)$.
$\mathcal{T}_{1,n}^n(\sigma, \mathbb{C},\mathbb{C}^d,\ldots,\mathbb{C}^d , H)$.
Remark 3.4. In the example above, instead of choosing ![]() $t_{i,j}$ to be the flip, we can choose any other isomorphism of
$t_{i,j}$ to be the flip, we can choose any other isomorphism of ![]() $\mathbb{C}^d\otimes \mathbb{C}^d$ (for i > j). Such an isomorphism is given by any unitary matrix of size
$\mathbb{C}^d\otimes \mathbb{C}^d$ (for i > j). Such an isomorphism is given by any unitary matrix of size ![]() $d^2\times d^2$. This will give us another, more involved, commutation relation (see, e.g., [Reference Power and Solel14,Equation (1).We will not go into details here except to note that if d = 1 and, for every i > j, we fix some number
$d^2\times d^2$. This will give us another, more involved, commutation relation (see, e.g., [Reference Power and Solel14,Equation (1).We will not go into details here except to note that if d = 1 and, for every i > j, we fix some number ![]() $u_{i,j}$ with
$u_{i,j}$ with ![]() $|u_{i,j}|=1$, then the commutation relation is
$|u_{i,j}|=1$, then the commutation relation is
for i > j. Note that if ![]() $(T_1,\ldots, T_n)$ is a tuple of contractions that u-commute (in the sense of equation (3.8)), then TG may depend on the order on G but
$(T_1,\ldots, T_n)$ is a tuple of contractions that u-commute (in the sense of equation (3.8)), then TG may depend on the order on G but ![]() $T_GT_{G}^*$ does not. In fact, in the expression of equation (3.1),
$T_GT_{G}^*$ does not. In fact, in the expression of equation (3.1), ![]() $u_{i,j}$ will get cancelled .
$u_{i,j}$ will get cancelled .
Example 3.5. If, in the setup of remark 3.4, we take d = 1 and ![]() $u_{i,j}=1$ for all
$u_{i,j}=1$ for all ![]() $i,j$, then it reduces to the case of a commuting tuple of contractions studied by many researchers (see the introduction). Note that, in this case, definition 2.8 reduces to definition 1.2.
$i,j$, then it reduces to the case of a commuting tuple of contractions studied by many researchers (see the introduction). Note that, in this case, definition 2.8 reduces to definition 1.2.
Let ![]() $(\sigma, T_1,\ldots,T_n)\in\mathcal{T}_{1,n}^n(\sigma, M, E_1,\ldots,E_n , H)$. Merging the
$(\sigma, T_1,\ldots,T_n)\in\mathcal{T}_{1,n}^n(\sigma, M, E_1,\ldots,E_n , H)$. Merging the ![]() $(n-1)$-tuples
$(n-1)$-tuples ![]() $\hat{T}_1$ and
$\hat{T}_1$ and ![]() $\hat{T}_n$, we consider a new
$\hat{T}_n$, we consider a new ![]() $(n-1)$-tuple
$(n-1)$-tuple ![]() $\hat{T}_{1n}$ in the following way:
$\hat{T}_{1n}$ in the following way:
 \begin{equation*}
\tilde{\hat{T}}_{1n}=\big(\tilde{T}_1(I_1\otimes \tilde{T}_n),\tilde{T_2},\ldots,\tilde{T}_{n-1}\big).
\end{equation*}
\begin{equation*}
\tilde{\hat{T}}_{1n}=\big(\tilde{T}_1(I_1\otimes \tilde{T}_n),\tilde{T_2},\ldots,\tilde{T}_{n-1}\big).
\end{equation*}We have the following result.
Proposition 3.6. If the tuples ![]() $\hat{T}_1$ and
$\hat{T}_1$ and ![]() $\hat{T}_n$ satisfy Szegö positivity, then so does
$\hat{T}_n$ satisfy Szegö positivity, then so does ![]() $\hat{T}_{1n}$. Moreover, denoting
$\hat{T}_{1n}$. Moreover, denoting
 \begin{align*}
D_{\hat{T}_i}:& =\mathbb{S}_{n-1}^{-1}\left(\tilde{\hat{T}}_i,\left(\tilde{\hat{T}}_i\right)^*\right)^{1/2}\quad(\text{for all}\,\, i=1,2)\,\, \quad\text{and}\nonumber\\
D_{\hat{T}_{1n}}:& =\mathbb{S}_{n-1}^{-1}\left(\tilde{\hat{T}}_{1n},\left(\tilde{\hat{T}}_{1n}\right)^*\right)^{1/2},
\end{align*}
\begin{align*}
D_{\hat{T}_i}:& =\mathbb{S}_{n-1}^{-1}\left(\tilde{\hat{T}}_i,\left(\tilde{\hat{T}}_i\right)^*\right)^{1/2}\quad(\text{for all}\,\, i=1,2)\,\, \quad\text{and}\nonumber\\
D_{\hat{T}_{1n}}:& =\mathbb{S}_{n-1}^{-1}\left(\tilde{\hat{T}}_{1n},\left(\tilde{\hat{T}}_{1n}\right)^*\right)^{1/2},
\end{align*}we have
 \begin{equation*}D_{\hat{T}_{1n}}^2=D_{\hat{T}_n} ^2+\tilde{T}_1(I_1\otimes D_{\hat{T}_1} ^2)(\tilde{T}_1)^*=D_{\hat{T}_1} ^2+\tilde{T_n}(I_n\otimes D_{\hat{T}_n} ^2)(\tilde{T_n})^*.\end{equation*}
\begin{equation*}D_{\hat{T}_{1n}}^2=D_{\hat{T}_n} ^2+\tilde{T}_1(I_1\otimes D_{\hat{T}_1} ^2)(\tilde{T}_1)^*=D_{\hat{T}_1} ^2+\tilde{T_n}(I_n\otimes D_{\hat{T}_n} ^2)(\tilde{T_n})^*.\end{equation*}Proof. We observe that
 \begin{align*}
&\mathbb{S}_{n-1}^{-1}\Big(\tilde{\hat{T}}_{1n},\left(\tilde{\hat{T}}_{1n}\right)^*\Big)\\
& \quad = \sum_{G \subset \{1,\ldots,n-1\}} (-1)^{|G|} \big(\tilde{\hat{T}}_{1n}\big)_G \big(\tilde{\hat{T}}_{1n}\big)_G^* \\
& \quad = \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} \tilde{T}_G \tilde{T}_G^*- \tilde{T}_1(I_1 \otimes \tilde{T}_n) \\
& \qquad \times \Big( \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) (I_1 \otimes (\tilde{T_n})^*) (\tilde{T}_1)^* \\
& \quad = \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} \tilde{T}_G \big(\tilde{T}_G\big)^*- \tilde{T}_1 \Big( \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} I_1\otimes \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) (\tilde{T}_1)^* \\
& \qquad + \tilde{T}_1 \Big( \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} I_1 \otimes \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) \tilde{T}_1^{*} \\
& \qquad - \tilde{T}_1(I_1 \otimes \tilde{T}_n) \Big( \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} I_{1n} \otimes \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) (I_1 \otimes (\tilde{T_n})^*) (\tilde{T}_1)^* \\
& \quad = \sum_{G \subset \{1,\ldots,n-1\}} (-1)^{|G|} \big(\tilde{\hat{T}}_{n}\big)_G \big(\tilde{\hat{T}}_{n}\big)_G^* + \tilde{T}_1 \\
& \qquad \times \Big(
I_1 \otimes \sum_{G \subset \{2,\ldots,n\}} (-1)^{|G|} \big(\tilde{\hat{T}}_{1}\big)_G \big(\tilde{\hat{T}}_{1}\big)_G^* \Big) (\tilde{T}_1)^* \\
& \quad = \mathbb{S}_{n-1}^{-1}\big(\tilde{\hat{T}}_{1},\big(\tilde{\hat{T}}_1\big)^*\big) + \tilde{T}_1 \Big( I_1 \otimes \mathbb{S}_{n-1}^{-1}\big(\tilde{\hat{T}}_{n},\big(\tilde{\hat{T}}_n\big)^*\big) \Big) (\tilde{T}_1)^* \\
& \quad = D_{\hat{T}_1}^2 + \tilde{T}_1\Big( I_1 \otimes D_{\hat{T}_n}^2 \Big) (\tilde{T}_1)^* .
\end{align*}
\begin{align*}
&\mathbb{S}_{n-1}^{-1}\Big(\tilde{\hat{T}}_{1n},\left(\tilde{\hat{T}}_{1n}\right)^*\Big)\\
& \quad = \sum_{G \subset \{1,\ldots,n-1\}} (-1)^{|G|} \big(\tilde{\hat{T}}_{1n}\big)_G \big(\tilde{\hat{T}}_{1n}\big)_G^* \\
& \quad = \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} \tilde{T}_G \tilde{T}_G^*- \tilde{T}_1(I_1 \otimes \tilde{T}_n) \\
& \qquad \times \Big( \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) (I_1 \otimes (\tilde{T_n})^*) (\tilde{T}_1)^* \\
& \quad = \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} \tilde{T}_G \big(\tilde{T}_G\big)^*- \tilde{T}_1 \Big( \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} I_1\otimes \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) (\tilde{T}_1)^* \\
& \qquad + \tilde{T}_1 \Big( \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} I_1 \otimes \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) \tilde{T}_1^{*} \\
& \qquad - \tilde{T}_1(I_1 \otimes \tilde{T}_n) \Big( \sum_{G \subset \{2,\ldots,n-1\}} (-1)^{|G|} I_{1n} \otimes \tilde{T}_G \big(\tilde{T}_G\big)^*\Big) (I_1 \otimes (\tilde{T_n})^*) (\tilde{T}_1)^* \\
& \quad = \sum_{G \subset \{1,\ldots,n-1\}} (-1)^{|G|} \big(\tilde{\hat{T}}_{n}\big)_G \big(\tilde{\hat{T}}_{n}\big)_G^* + \tilde{T}_1 \\
& \qquad \times \Big(
I_1 \otimes \sum_{G \subset \{2,\ldots,n\}} (-1)^{|G|} \big(\tilde{\hat{T}}_{1}\big)_G \big(\tilde{\hat{T}}_{1}\big)_G^* \Big) (\tilde{T}_1)^* \\
& \quad = \mathbb{S}_{n-1}^{-1}\big(\tilde{\hat{T}}_{1},\big(\tilde{\hat{T}}_1\big)^*\big) + \tilde{T}_1 \Big( I_1 \otimes \mathbb{S}_{n-1}^{-1}\big(\tilde{\hat{T}}_{n},\big(\tilde{\hat{T}}_n\big)^*\big) \Big) (\tilde{T}_1)^* \\
& \quad = D_{\hat{T}_1}^2 + \tilde{T}_1\Big( I_1 \otimes D_{\hat{T}_n}^2 \Big) (\tilde{T}_1)^* .
\end{align*}So,
 \begin{equation*}
\mathbb{S}_{n-1}^{-1}\left(\tilde{\hat{T}}_{1n},\left(\tilde{\hat{T}}_{1n}\right)^*\right)\geq 0
\end{equation*}
\begin{equation*}
\mathbb{S}_{n-1}^{-1}\left(\tilde{\hat{T}}_{1n},\left(\tilde{\hat{T}}_{1n}\right)^*\right)\geq 0
\end{equation*}and hence
 \begin{equation*}
D_{\hat{T}_{1n}}^2 =D_{\hat{T}_1}^2 + \tilde{T}_n\Big( I_n \otimes D_{\hat{T}_n}^2 \Big) (\tilde{T}_n)^*.
\end{equation*}
\begin{equation*}
D_{\hat{T}_{1n}}^2 =D_{\hat{T}_1}^2 + \tilde{T}_n\Big( I_n \otimes D_{\hat{T}_n}^2 \Big) (\tilde{T}_n)^*.
\end{equation*}Similarly, we can also show that
 \begin{equation*}
D_{\hat{T}_{1n}}^2 = D_{\hat{T}_n}^2 + \tilde{T}_1\Big( I_1 \otimes D_{\hat{T}_1}^2 \Big) (\tilde{T_1})^*.
\end{equation*}
\begin{equation*}
D_{\hat{T}_{1n}}^2 = D_{\hat{T}_n}^2 + \tilde{T}_1\Big( I_1 \otimes D_{\hat{T}_1}^2 \Big) (\tilde{T_1})^*.
\end{equation*} From the above proposition, it follows that for every ![]() $h\in H$,
$h\in H$,
 \begin{equation}
\|D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\|=\| D_{\hat{T}_1} h\oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h\|.
\end{equation}
\begin{equation}
\|D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\|=\| D_{\hat{T}_1} h\oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h\|.
\end{equation} Note that  $\{D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h : h\in H\}$ is a subspace of
$\{D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h : h\in H\}$ is a subspace of ![]() $H\oplus (E_1\otimes H)$. On
$H\oplus (E_1\otimes H)$. On ![]() $H\oplus (E_1\otimes H)$, we have a representation τ 1 of M where, for
$H\oplus (E_1\otimes H)$, we have a representation τ 1 of M where, for ![]() $h,k\in H$ and
$h,k\in H$ and ![]() $a\in M$,
$a\in M$,
and τ 2 is defined similarly on ![]() $H\oplus (E_n\otimes H)$.
$H\oplus (E_n\otimes H)$.
Note that  $D_{\tilde{T_i}}$ commutes with
$D_{\tilde{T_i}}$ commutes with ![]() $\sigma(M)$, and for
$\sigma(M)$, and for ![]() $a\in M$,
$a\in M$, ![]() $(\tilde{T}_i)^*\sigma(a)=(\varphi_i(a)\otimes I_H)(\tilde{T}_i)^*$. It follows that
$(\tilde{T}_i)^*\sigma(a)=(\varphi_i(a)\otimes I_H)(\tilde{T}_i)^*$. It follows that
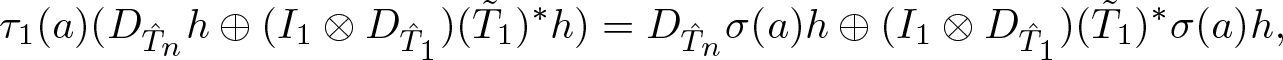 \begin{equation*}\tau_1(a)( D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h)= D_{\hat{T}_n} \sigma(a)h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*\sigma(a)h,\end{equation*}
\begin{equation*}\tau_1(a)( D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h)= D_{\hat{T}_n} \sigma(a)h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*\sigma(a)h,\end{equation*} and therefore, the space  $\{D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h : h\in H\}$ is invariant under
$\{D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h : h\in H\}$ is invariant under ![]() $\tau_1(M)$. Writing
$\tau_1(M)$. Writing ![]() $\mathcal{D}_1$ for the closure
$\mathcal{D}_1$ for the closure
 \begin{equation}
\mathcal{D}_1=\{D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h : h\in H\}^-,
\end{equation}
\begin{equation}
\mathcal{D}_1=\{D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h : h\in H\}^-,
\end{equation}we see that restricting τ 1 to it, we get a subrepresentation of τ 1. Similarly, setting
 \begin{equation}
\mathcal{D}_2=\{D_{\hat{T}_1} h\oplus (I_n\otimes D_{\hat{T}_n})(\tilde{T_n})^*h : h\in H\}^-,
\end{equation}
\begin{equation}
\mathcal{D}_2=\{D_{\hat{T}_1} h\oplus (I_n\otimes D_{\hat{T}_n})(\tilde{T_n})^*h : h\in H\}^-,
\end{equation}we get a subrepresentation of τ 2.
It follows from (3.9) that we can define a partial isometry (with initial space ![]() $\mathcal{D}_1$)
$\mathcal{D}_1$)
by
 \begin{equation*}V_0(D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h)=D_{\hat{T}_1} h\oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h.\end{equation*}
\begin{equation*}V_0(D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h)=D_{\hat{T}_1} h\oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h.\end{equation*}From the above definition, it is straightforward to see that V 0 intertwines τ 1 and τ 2. That is,
for all ![]() $a \in M$, and we can write
$a \in M$, and we can write
In the next proposition, we show that by extending the spaces ![]() $\mathcal{D}_1$ and
$\mathcal{D}_1$ and ![]() $\mathcal{D}_2$ suitably, one can define a unitary that extends V 0 and intertwines representations of M on those extended spaces. For the next proposition, the closure of the range of
$\mathcal{D}_2$ suitably, one can define a unitary that extends V 0 and intertwines representations of M on those extended spaces. For the next proposition, the closure of the range of  $D_{\hat{T_i}}$, for
$D_{\hat{T_i}}$, for ![]() $i=1,2$, is denoted by
$i=1,2$, is denoted by  $\mathcal{D}_{\hat{T_i}}$. That will also be used throughout the article.
$\mathcal{D}_{\hat{T_i}}$. That will also be used throughout the article.
Proposition 3.7. We can find representations ![]() $\rho_1, \rho_2$ of M on Hilbert spaces
$\rho_1, \rho_2$ of M on Hilbert spaces ![]() $\mathcal{E}_1, \mathcal{E}_2$ and a unitary operator
$\mathcal{E}_1, \mathcal{E}_2$ and a unitary operator
 \begin{equation*}U: \mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \end{equation*}
\begin{equation*}U: \mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \end{equation*} that extends ![]() $U_0:=V_0^{-1}$ and intertwines the representations of M. Moreover,
$U_0:=V_0^{-1}$ and intertwines the representations of M. Moreover,
(i) there is a unitary operator
 $u_1:E_1 \otimes \mathcal{E}_2 \rightarrow \mathcal{E}_1$ (so that
$u_1:E_1 \otimes \mathcal{E}_2 \rightarrow \mathcal{E}_1$ (so that  $u_1(E_1\otimes \mathcal{E}_2)= \mathcal{E}_1 $) that intertwines the representations ρ 1 and
$u_1(E_1\otimes \mathcal{E}_2)= \mathcal{E}_1 $) that intertwines the representations ρ 1 and  $\varphi_1(\cdot)\otimes_{\rho_2}I_{\mathcal{E}_2}$.
$\varphi_1(\cdot)\otimes_{\rho_2}I_{\mathcal{E}_2}$.(ii) there is a unitary operator
 $u_2: \mathcal{E}_2 \rightarrow E_n \otimes\mathcal{E}_1$ (so that
$u_2: \mathcal{E}_2 \rightarrow E_n \otimes\mathcal{E}_1$ (so that  $u_2\mathcal{E}_2=E_n\otimes \mathcal{E}_1 $) that intertwines the representations ρ 2 and
$u_2\mathcal{E}_2=E_n\otimes \mathcal{E}_1 $) that intertwines the representations ρ 2 and  $\varphi_2(\cdot)\otimes_{\rho_1}I_{\mathcal{E}_1}$.
$\varphi_2(\cdot)\otimes_{\rho_1}I_{\mathcal{E}_1}$.(iii)
 $\mathcal{E}_i$ (
$\mathcal{E}_i$ ( $i=1,2$) are infinite generators of NRep(M).
$i=1,2$) are infinite generators of NRep(M).
Proof. We observe
 \begin{equation*}\mathcal{D}_1\subseteq \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} ) \end{equation*}
\begin{equation*}\mathcal{D}_1\subseteq \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} ) \end{equation*}and
 \begin{equation*}\mathcal{D}_2\subseteq \mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} ) .\end{equation*}
\begin{equation*}\mathcal{D}_2\subseteq \mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} ) .\end{equation*}Note that the spaces on the right are also invariant under τ 1 (or τ 2), so they are (left) M-modules and so are
 \begin{equation*}\mathcal{M}_2:=\mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\ominus \mathcal{D}_2\end{equation*}
\begin{equation*}\mathcal{M}_2:=\mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\ominus \mathcal{D}_2\end{equation*}and
 \begin{equation*}\mathcal{M}_1:=\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\ominus \mathcal{D}_1.\end{equation*}
\begin{equation*}\mathcal{M}_1:=\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\ominus \mathcal{D}_1.\end{equation*}Now we write,
(for ![]() $i=1,2$) infinite generators. It follows that
$i=1,2$) infinite generators. It follows that ![]() $E_n\otimes \mathcal{E}_1$ and
$E_n\otimes \mathcal{E}_1$ and ![]() $E_1\otimes \mathcal{E}_2$ are also infinite generators. The uniqueness of infinite generators implies the existence of
$E_1\otimes \mathcal{E}_2$ are also infinite generators. The uniqueness of infinite generators implies the existence of ![]() $u_1,u_2$ satisfying (i) and (ii).
$u_1,u_2$ satisfying (i) and (ii).
Since ![]() $\mathcal{E}_1\precsim \mathcal{M}_i \oplus \mathcal{E}_i$,
$\mathcal{E}_1\precsim \mathcal{M}_i \oplus \mathcal{E}_i$, ![]() $\mathcal{M}_i \oplus\mathcal{E}_i$ is also an infinite generator and it follows from the uniqueness that there is a unitary operator u 1 from
$\mathcal{M}_i \oplus\mathcal{E}_i$ is also an infinite generator and it follows from the uniqueness that there is a unitary operator u 1 from ![]() $\mathcal{M}_2\oplus \mathcal{E}_2$ onto
$\mathcal{M}_2\oplus \mathcal{E}_2$ onto ![]() $\mathcal{M}_1\oplus \mathcal{E}_1$ that intertwines the representations. Setting
$\mathcal{M}_1\oplus \mathcal{E}_1$ that intertwines the representations. Setting ![]() $U=V_0^*\oplus u_1$ completes the proof.
$U=V_0^*\oplus u_1$ completes the proof.
To simplify the notation, we write Eij for ![]() $E_i\otimes E_j$ and identify it with
$E_i\otimes E_j$ and identify it with ![]() $E_j\otimes E_i$. Similarly, we write Eijk for
$E_j\otimes E_i$. Similarly, we write Eijk for ![]() $E_i\otimes E_j\otimes E_k$, etc.
$E_i\otimes E_j\otimes E_k$, etc.
We have from the proposition 3.6 that
 \begin{equation*}D_{\hat{T}_{1n}}^2=D_{\hat{T}_n} ^2+\tilde{T_1}(I_1\otimes D_{\hat{T}_1} ^2)(\tilde{T}_1)^*=D_{\hat{T}_1} ^2+\tilde{T_n}(I_n\otimes D_{\hat{T}_n} ^2)(\tilde{T_n})^*\geq 0.\end{equation*}
\begin{equation*}D_{\hat{T}_{1n}}^2=D_{\hat{T}_n} ^2+\tilde{T_1}(I_1\otimes D_{\hat{T}_1} ^2)(\tilde{T}_1)^*=D_{\hat{T}_1} ^2+\tilde{T_n}(I_n\otimes D_{\hat{T}_n} ^2)(\tilde{T_n})^*\geq 0.\end{equation*} We, thus, get an isometry  $V:\mathcal{D}_{\hat{T}_{1n}}\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 $ such that
$V:\mathcal{D}_{\hat{T}_{1n}}\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 $ such that
 \begin{equation*}V(D_{\hat{T}_{1n}}h)=D_{\hat{T}_n} h \oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}.\end{equation*}
\begin{equation*}V(D_{\hat{T}_{1n}}h)=D_{\hat{T}_n} h \oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}.\end{equation*}We now need the following notations:
(i) P 1 is the projection
 \begin{equation*}P_1:\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \rightarrow E_1\otimes \mathcal{D}_{\hat{T}_1} .\end{equation*}
\begin{equation*}P_1:\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \rightarrow E_1\otimes \mathcal{D}_{\hat{T}_1} .\end{equation*}(ii)
 $i_2'$ is the inclusion
$i_2'$ is the inclusion
 \begin{equation*}i_2':(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_1 \otimes \mathcal{E}_2) \rightarrow (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_1 \otimes \mathcal{E}_2) .\end{equation*}
\begin{equation*}i_2':(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_1 \otimes \mathcal{E}_2) \rightarrow (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_1 \otimes \mathcal{E}_2) .\end{equation*}(iii)
 $j_2'=i_2'\circ (I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*)): (E_{1n}\otimes \mathcal{D}_{\hat{T}_n})\oplus (E_{1n}\otimes \mathcal{E}_1)\rightarrow (E_{1n}\otimes \mathcal{D}_{\hat{T}_n})\oplus (E_1\otimes \mathcal{E}_2)\oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )$.
$j_2'=i_2'\circ (I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*)): (E_{1n}\otimes \mathcal{D}_{\hat{T}_n})\oplus (E_{1n}\otimes \mathcal{E}_1)\rightarrow (E_{1n}\otimes \mathcal{D}_{\hat{T}_n})\oplus (E_1\otimes \mathcal{E}_2)\oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )$.(iv) i 2 is the inclusion
 \begin{equation*}i_2:\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 \rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \oplus \mathcal{E}_1,\end{equation*}
\begin{equation*}i_2:\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 \rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \oplus \mathcal{E}_1,\end{equation*}so that
 $i_2^*$ is the projection
$i_2^*$ is the projection
 \begin{equation*}i_2^*:\mathcal{D}_{\hat{T}_n} \oplus (E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \oplus \mathcal{E}_1 \rightarrow \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 .\end{equation*}
\begin{equation*}i_2^*:\mathcal{D}_{\hat{T}_n} \oplus (E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \oplus \mathcal{E}_1 \rightarrow \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 .\end{equation*}
Note that, since U intertwines the representations of M, the operator ![]() $I_1 \otimes U$ is well defined and bounded. So the following operators are well defined:
$I_1 \otimes U$ is well defined and bounded. So the following operators are well defined:
 \begin{equation*}(I_1\otimes U)P_1:\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \rightarrow (E_1\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1 \otimes E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_1\otimes \mathcal{E}_1) \end{equation*}
\begin{equation*}(I_1\otimes U)P_1:\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \rightarrow (E_1\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1 \otimes E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_1\otimes \mathcal{E}_1) \end{equation*}and
 \begin{equation*}(I_1\otimes U)j_2':(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_{1n} \otimes \mathcal{E}_1)\rightarrow (E_1\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} )\oplus( E_1\otimes \mathcal{E}_1 ).\end{equation*}
\begin{equation*}(I_1\otimes U)j_2':(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_{1n} \otimes \mathcal{E}_1)\rightarrow (E_1\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} )\oplus( E_1\otimes \mathcal{E}_1 ).\end{equation*}We can now form the operator
 \begin{align} U_1: = \left(\begin{array}{cc} (I_1\otimes U)P_1 & (I_1\otimes U)j_2' \\ i_2^* & 0 \end{array}\right) : \left(\begin{array}{c} \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \\ (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_{1n} \otimes \mathcal{E}_1) \end{array}\right) \end{align}
\begin{align} U_1: = \left(\begin{array}{cc} (I_1\otimes U)P_1 & (I_1\otimes U)j_2' \\ i_2^* & 0 \end{array}\right) : \left(\begin{array}{c} \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \\ (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_{1n} \otimes \mathcal{E}_1) \end{array}\right) \end{align} \begin{equation*}\rightarrow \left(\begin{array}{c} (E_1\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} )\oplus ( E_1\otimes \mathcal{E}_1 )\\ \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 \end{array}\right). \end{equation*}
\begin{equation*}\rightarrow \left(\begin{array}{c} (E_1\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} )\oplus ( E_1\otimes \mathcal{E}_1 )\\ \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 \end{array}\right). \end{equation*}A straightforward computation shows that as U is unitary, then so is U 1.
To shorten some computations, we shall write
 \begin{equation} \mathcal{D}:=\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1
\end{equation}
\begin{equation} \mathcal{D}:=\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1
\end{equation}and
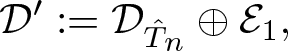 \begin{equation} \mathcal{D}':=\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1,
\end{equation}
\begin{equation} \mathcal{D}':=\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1,
\end{equation}so that
 \begin{equation*}U_1:= \left(\begin{array}{cc} (I_1\otimes U)P_1 & (I_1\otimes U)j_2' \\ i_2^* & 0 \end{array}\right) : \left(\begin{array}{c} \mathcal{D} \\ E_{1n} \otimes \mathcal{D}' \end{array}\right) \rightarrow \left(\begin{array}{c} E_1\otimes \mathcal{D}\\ \mathcal{D}' \end{array}\right). \end{equation*}
\begin{equation*}U_1:= \left(\begin{array}{cc} (I_1\otimes U)P_1 & (I_1\otimes U)j_2' \\ i_2^* & 0 \end{array}\right) : \left(\begin{array}{c} \mathcal{D} \\ E_{1n} \otimes \mathcal{D}' \end{array}\right) \rightarrow \left(\begin{array}{c} E_1\otimes \mathcal{D}\\ \mathcal{D}' \end{array}\right). \end{equation*} Note that M acts on ![]() $\mathcal{D}$ by the restriction, to
$\mathcal{D}$ by the restriction, to ![]() $\mathcal{D}$, of
$\mathcal{D}$, of  $\sigma \oplus ( \varphi_1 \otimes I_{\mathcal{D}_{\hat{T}_1}})\oplus \rho_1$ we write
$\sigma \oplus ( \varphi_1 \otimes I_{\mathcal{D}_{\hat{T}_1}})\oplus \rho_1$ we write ![]() $\rho_{\mathcal{D}}$ for this representation. Similarly,
$\rho_{\mathcal{D}}$ for this representation. Similarly, ![]() $\rho_{\mathcal{D}'}$ will denote the representation of M on
$\rho_{\mathcal{D}'}$ will denote the representation of M on ![]() $\mathcal{D}'$ (the restriction of
$\mathcal{D}'$ (the restriction of ![]() $\sigma \oplus \rho_1$). There is a natural left action on
$\sigma \oplus \rho_1$). There is a natural left action on ![]() $E_{1n}=E_1\otimes E_n$, which comes through an adjointable map
$E_{1n}=E_1\otimes E_n$, which comes through an adjointable map ![]() $\varphi_{1n}: M\to \mathcal{L}(E_1\otimes E_n)$, which is defined by
$\varphi_{1n}: M\to \mathcal{L}(E_1\otimes E_n)$, which is defined by
Viewing ![]() $E_{1n}$ as
$E_{1n}$ as ![]() $E_n\otimes E_1$, the action
$E_n\otimes E_1$, the action ![]() $\varphi_{1n}$ can also be represented by
$\varphi_{1n}$ can also be represented by
We have the following lemma:
Lemma 3.8. The operator U 1 intertwines the representations of M, that is,
for every ![]() $a\in M$.
$a\in M$.
Proof. We need to prove the following for every ![]() $a\in M$:
$a\in M$:
(i)
 $(I_1\otimes U)P_1 \rho_{\mathcal{D}}(a)=((\varphi_1(a)\otimes I_{\mathcal{D}})(I_1\otimes U)P_1 $.
$(I_1\otimes U)P_1 \rho_{\mathcal{D}}(a)=((\varphi_1(a)\otimes I_{\mathcal{D}})(I_1\otimes U)P_1 $.(ii)
 $((I_1\otimes U)j_2') (\varphi_{1n}(a)\otimes I_{\mathcal{D}'})=(\varphi_1(a)\otimes I_{\mathcal{D}})((I_1\otimes U)j_2')$.
$((I_1\otimes U)j_2') (\varphi_{1n}(a)\otimes I_{\mathcal{D}'})=(\varphi_1(a)\otimes I_{\mathcal{D}})((I_1\otimes U)j_2')$.(iii)
 $i_2^* \rho_{\mathcal{D}}(a)=\rho_{\mathcal{D}'}(a)i_2^*$.
$i_2^* \rho_{\mathcal{D}}(a)=\rho_{\mathcal{D}'}(a)i_2^*$.
Part (iii) is obvious. We proceed to prove part (i). From the definitions of P 1 and of ![]() $\rho_{\mathcal{D}}$, it follows that
$\rho_{\mathcal{D}}$, it follows that
 \begin{equation*}P_1\rho_{\mathcal{D}}(a)=(\varphi_1(a) \otimes I_{\mathcal{D}_{\hat{T}_1}})P_1.\end{equation*}
\begin{equation*}P_1\rho_{\mathcal{D}}(a)=(\varphi_1(a) \otimes I_{\mathcal{D}_{\hat{T}_1}})P_1.\end{equation*} It follows from proposition 3.7 that  $U\sigma|\mathcal{D}_{\tilde{T}_2}=\rho_{\mathcal{D}}U|\mathcal{D}_{\tilde{T}_2}$. Using this, we have
$U\sigma|\mathcal{D}_{\tilde{T}_2}=\rho_{\mathcal{D}}U|\mathcal{D}_{\tilde{T}_2}$. Using this, we have
 \begin{equation*}(I_1\otimes U)P_1\rho_{\mathcal{D}}(a)=(I_1\otimes U)(\varphi_1(a) \otimes I_{\mathcal{D}_{\hat{T}_1}})P_1=(\varphi_1(a) \otimes I_{\mathcal{D}})(I_1\otimes U)P_1 ,\end{equation*}
\begin{equation*}(I_1\otimes U)P_1\rho_{\mathcal{D}}(a)=(I_1\otimes U)(\varphi_1(a) \otimes I_{\mathcal{D}_{\hat{T}_1}})P_1=(\varphi_1(a) \otimes I_{\mathcal{D}})(I_1\otimes U)P_1 ,\end{equation*}proving (i). For (ii), we write
 \begin{equation*}((I_1\otimes U)j_2') (\varphi_{1n}(a)\otimes I_{\mathcal{D}'})=(I_1\otimes U)i_2'(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*))(\varphi_{1n}(a)\otimes I_{\mathcal{D}'})\end{equation*}
\begin{equation*}((I_1\otimes U)j_2') (\varphi_{1n}(a)\otimes I_{\mathcal{D}'})=(I_1\otimes U)i_2'(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*))(\varphi_{1n}(a)\otimes I_{\mathcal{D}'})\end{equation*} \begin{equation*}=(I_1\otimes U)i_2'((\varphi_{1n}(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus (\varphi_1(a)\otimes I_{\mathcal{E}_2}))(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*))\end{equation*}
\begin{equation*}=(I_1\otimes U)i_2'((\varphi_{1n}(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus (\varphi_1(a)\otimes I_{\mathcal{E}_2}))(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*))\end{equation*} \begin{equation*}=(I_1\otimes U)((\varphi_{1n}(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus (\varphi_1(a)\otimes I_{\mathcal{E}_2})\oplus (\varphi_1(a)\otimes I_{\mathcal{D}_{\hat{T}_1}}))i_2'(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*)).\end{equation*}
\begin{equation*}=(I_1\otimes U)((\varphi_{1n}(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus (\varphi_1(a)\otimes I_{\mathcal{E}_2})\oplus (\varphi_1(a)\otimes I_{\mathcal{D}_{\hat{T}_1}}))i_2'(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*)).\end{equation*}Using the intertwining property of U again, we see that this is equal to
 \begin{equation*}(\varphi_1(a) \otimes I_{\mathcal{D}})(I_1\otimes U)i_2'(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*))=(\varphi_1(a)\otimes I_{\mathcal{D}})((I_1\otimes U)j_2'),\end{equation*}
\begin{equation*}(\varphi_1(a) \otimes I_{\mathcal{D}})(I_1\otimes U)i_2'(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_n}}\oplus (I_1\otimes u_2^*))=(\varphi_1(a)\otimes I_{\mathcal{D}})((I_1\otimes U)j_2'),\end{equation*}proving (ii).
Lemma 3.9. For ![]() $h\in H$,
$h\in H$,
 \begin{align*}& U_1(VD_{\hat{T}_{1n}}h, (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\oplus 0_{E_{1n}\otimes \mathcal{E}_1})\\
& \quad =((I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h, D_{\hat{T}_n} h\oplus 0_{\mathcal{E}_1}).\end{align*}
\begin{align*}& U_1(VD_{\hat{T}_{1n}}h, (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\oplus 0_{E_{1n}\otimes \mathcal{E}_1})\\
& \quad =((I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h, D_{\hat{T}_n} h\oplus 0_{\mathcal{E}_1}).\end{align*}Proof. We start by proving that, for ![]() $f\in E_1\otimes H$,
$f\in E_1\otimes H$,
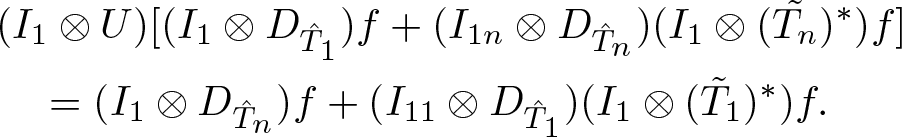 \begin{align}
& (I_1\otimes U)[(I_1\otimes D_{\hat{T}_1} )f+ (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)f]\nonumber\\& \quad=(I_1\otimes D_{\hat{T}_n} )f+(I_{11}\otimes D_{\hat{T}_1} )(I_1\otimes (\tilde{T}_1)^*)f.
\end{align}
\begin{align}
& (I_1\otimes U)[(I_1\otimes D_{\hat{T}_1} )f+ (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)f]\nonumber\\& \quad=(I_1\otimes D_{\hat{T}_n} )f+(I_{11}\otimes D_{\hat{T}_1} )(I_1\otimes (\tilde{T}_1)^*)f.
\end{align} Clearly, it suffices to prove it for ![]() $f=\xi \otimes g$, where
$f=\xi \otimes g$, where ![]() $\xi\in E_1$ and
$\xi\in E_1$ and ![]() $g\in H$. So, we compute
$g\in H$. So, we compute
 \begin{align*}
&(I_1\otimes U)[(I_1\otimes D_{\hat{T}_1} )(\xi\otimes g)\oplus (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\xi\otimes g)\oplus 0_{E_1\otimes \mathcal{E}_2}]\\
& \quad = (I_1\otimes U)[\xi \otimes D_{\hat{T}_1} g \oplus(I_{1n}\otimes D_{\hat{T}_n} )(\xi\otimes (\tilde{T_n})^*g)\oplus 0_{E_1\otimes \mathcal{E}_2}]\\
& \quad = (I_1\otimes U)[\xi \otimes D_{\hat{T}_1} g \oplus \xi \otimes (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*g \oplus 0_{E_1\otimes \mathcal{E}_2}]\\
& \quad = \xi \otimes U(D_{\hat{T}_1} g \oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*g \oplus 0_{\mathcal{E}_2}).
\end{align*}
\begin{align*}
&(I_1\otimes U)[(I_1\otimes D_{\hat{T}_1} )(\xi\otimes g)\oplus (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\xi\otimes g)\oplus 0_{E_1\otimes \mathcal{E}_2}]\\
& \quad = (I_1\otimes U)[\xi \otimes D_{\hat{T}_1} g \oplus(I_{1n}\otimes D_{\hat{T}_n} )(\xi\otimes (\tilde{T_n})^*g)\oplus 0_{E_1\otimes \mathcal{E}_2}]\\
& \quad = (I_1\otimes U)[\xi \otimes D_{\hat{T}_1} g \oplus \xi \otimes (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*g \oplus 0_{E_1\otimes \mathcal{E}_2}]\\
& \quad = \xi \otimes U(D_{\hat{T}_1} g \oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*g \oplus 0_{\mathcal{E}_2}).
\end{align*} Since U extends U 0 (![]() $=V_0^{-1}$), we have
$=V_0^{-1}$), we have  $U(D_{\hat{T}_1} g \oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*g \oplus 0_{\mathcal{E}_2})=(D_{\hat{T}_n} g\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*g \oplus 0_{\mathcal{E}_1})$ and, thus,
$U(D_{\hat{T}_1} g \oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*g \oplus 0_{\mathcal{E}_2})=(D_{\hat{T}_n} g\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*g \oplus 0_{\mathcal{E}_1})$ and, thus,
 \begin{align*}
& (I_1\otimes U)[(I_1\otimes D_{\hat{T}_1} )(\xi\otimes g)\oplus (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\xi\otimes g)\oplus 0_{E_1\otimes \mathcal{E}_2}]\\
& \quad =\xi \otimes( D_{\hat{T}_n} g\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*g\oplus 0_{\mathcal{E}_1})\\
& \quad =(I_1\otimes D_{\hat{T}_n} )(\xi\otimes g)\oplus (I_{11}\otimes D_{\hat{T}_1} )(I_1\otimes (\tilde{T}_1)^*)(\xi\otimes g) \oplus 0_{E_1\otimes \mathcal{E}_1},
\end{align*}
\begin{align*}
& (I_1\otimes U)[(I_1\otimes D_{\hat{T}_1} )(\xi\otimes g)\oplus (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\xi\otimes g)\oplus 0_{E_1\otimes \mathcal{E}_2}]\\
& \quad =\xi \otimes( D_{\hat{T}_n} g\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*g\oplus 0_{\mathcal{E}_1})\\
& \quad =(I_1\otimes D_{\hat{T}_n} )(\xi\otimes g)\oplus (I_{11}\otimes D_{\hat{T}_1} )(I_1\otimes (\tilde{T}_1)^*)(\xi\otimes g) \oplus 0_{E_1\otimes \mathcal{E}_1},
\end{align*}proving (3.17).
Now we compute
 \begin{align*}
& U_1(VD_{\hat{T}_{1n}}h, (I_{1n}\otimes D_{\tilde{T}_1})(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\oplus 0_{E_{1n}\otimes \mathcal{E}_1})\\
& \quad = U_1(D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}, (I_{1n}\otimes D_{\hat{T}_n} )\\
& \qquad \times (I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h\oplus 0_{E_{1n}\otimes \mathcal{E}_1})\\
& \quad = ((I_1\otimes U)[(I_1\otimes D_{\tilde{T_n}})(\tilde{T}_1)^*h\oplus (I_{1n}\otimes D_{\hat{T}_n} )\\
& \qquad \times (I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\oplus 0_{E_1\otimes \mathcal{E}_2}], D_{\hat{T}_n} h\oplus 0_{\mathcal{E}_1})\\
& \quad =((I_1\otimes D_{\hat{T}_n} )(\tilde{T}_1)^*h\oplus (I_{11}\otimes D_{\hat{T}_1} )(I_1\otimes (\tilde{T}_1)^*)(\tilde{T}_1)^*h \oplus 0_{E_1\otimes \mathcal{E}_1}, D_{\hat{T}_n} h\ \oplus 0_{\mathcal{E}_1}),
\end{align*}
\begin{align*}
& U_1(VD_{\hat{T}_{1n}}h, (I_{1n}\otimes D_{\tilde{T}_1})(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\oplus 0_{E_{1n}\otimes \mathcal{E}_1})\\
& \quad = U_1(D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}, (I_{1n}\otimes D_{\hat{T}_n} )\\
& \qquad \times (I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h\oplus 0_{E_{1n}\otimes \mathcal{E}_1})\\
& \quad = ((I_1\otimes U)[(I_1\otimes D_{\tilde{T_n}})(\tilde{T}_1)^*h\oplus (I_{1n}\otimes D_{\hat{T}_n} )\\
& \qquad \times (I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\oplus 0_{E_1\otimes \mathcal{E}_2}], D_{\hat{T}_n} h\oplus 0_{\mathcal{E}_1})\\
& \quad =((I_1\otimes D_{\hat{T}_n} )(\tilde{T}_1)^*h\oplus (I_{11}\otimes D_{\hat{T}_1} )(I_1\otimes (\tilde{T}_1)^*)(\tilde{T}_1)^*h \oplus 0_{E_1\otimes \mathcal{E}_1}, D_{\hat{T}_n} h\ \oplus 0_{\mathcal{E}_1}),
\end{align*} where we used equation (3.17) with ![]() $f=(\tilde{T}_1)^*h$. It is left to show that
$f=(\tilde{T}_1)^*h$. It is left to show that
 \begin{align*}& (I_1\otimes D_{\hat{T}_n} )(\tilde{T}_1)^*h\oplus (I_{11}\otimes D_{\hat{T}_1} )(I_1\otimes (\tilde{T}_1)^*)(\tilde{T}_1)^*h \oplus 0_{E_1\otimes \mathcal{E}_1}\\
& \quad =(I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h.\end{align*}
\begin{align*}& (I_1\otimes D_{\hat{T}_n} )(\tilde{T}_1)^*h\oplus (I_{11}\otimes D_{\hat{T}_1} )(I_1\otimes (\tilde{T}_1)^*)(\tilde{T}_1)^*h \oplus 0_{E_1\otimes \mathcal{E}_1}\\
& \quad =(I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h.\end{align*} Now, replace ![]() $(\tilde{T}_1)^*h$ by
$(\tilde{T}_1)^*h$ by ![]() $\xi \otimes g$ and use the definition of V, that completes the proof.
$\xi \otimes g$ and use the definition of V, that completes the proof.
For faithful ![]() $W^*$-correspondences
$W^*$-correspondences ![]() $E_1,\ldots, E_n$ over a
$E_1,\ldots, E_n$ over a ![]() $W^*$-algebra M, we consider a new family of n − 1 faithful correspondences
$W^*$-algebra M, we consider a new family of n − 1 faithful correspondences ![]() $E_{1n}, E_2,\ldots ,E_{n-1}$. Now the Fock correspondence for this product system (constructed as in (2.6)) is
$E_{1n}, E_2,\ldots ,E_{n-1}$. Now the Fock correspondence for this product system (constructed as in (2.6)) is
 \begin{equation}
\mathcal{F}(E) = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} E^{\alpha},
\end{equation}
\begin{equation}
\mathcal{F}(E) = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} E^{\alpha},
\end{equation} where ![]() $E^0 = M$, and for each
$E^0 = M$, and for each  $0 \neq \alpha = (\alpha_1,\ldots,\alpha_{n-1}) \in \mathbb{Z}_+^{n-1}$,
$0 \neq \alpha = (\alpha_1,\ldots,\alpha_{n-1}) \in \mathbb{Z}_+^{n-1}$,  $E^{\alpha} = E_{1n}^{\otimes \alpha_1} \otimes E_2^{\otimes \alpha_2} \otimes \cdots \otimes E_{n-1}^{\otimes \alpha_{n-1}}$. For each
$E^{\alpha} = E_{1n}^{\otimes \alpha_1} \otimes E_2^{\otimes \alpha_2} \otimes \cdots \otimes E_{n-1}^{\otimes \alpha_{n-1}}$. For each ![]() $i \in \{2,\ldots,n-1\}$, we consider the left creation operator
$i \in \{2,\ldots,n-1\}$, we consider the left creation operator ![]() $L_i: E_i \to \mathcal{B}(\mathcal{F}(E)\otimes H)$ defined by
$L_i: E_i \to \mathcal{B}(\mathcal{F}(E)\otimes H)$ defined by
and ![]() $L_1: E_{1n} \to \mathcal{B}(\mathcal{F}(E)\otimes H)$ by
$L_1: E_{1n} \to \mathcal{B}(\mathcal{F}(E)\otimes H)$ by ![]() $L_1(\xi_{1n})= L_{\xi_{1n}}$ The operators
$L_1(\xi_{1n})= L_{\xi_{1n}}$ The operators ![]() $L_{\xi_i}: \mathcal{F}(E)\otimes H \to \mathcal{F}(E)\otimes H$ are defined by
$L_{\xi_i}: \mathcal{F}(E)\otimes H \to \mathcal{F}(E)\otimes H$ are defined by
 \begin{equation*}
L_{\xi_i}(h)=\xi_i \otimes h\quad \quad \text{and}\quad L_{\xi_i}(\eta^{(\alpha)}\otimes h)=\xi_i \otimes \eta^{(\alpha)}\otimes h\quad (\eta^{(\alpha)}\in E^{\alpha}, h\in H).
\end{equation*}
\begin{equation*}
L_{\xi_i}(h)=\xi_i \otimes h\quad \quad \text{and}\quad L_{\xi_i}(\eta^{(\alpha)}\otimes h)=\xi_i \otimes \eta^{(\alpha)}\otimes h\quad (\eta^{(\alpha)}\in E^{\alpha}, h\in H).
\end{equation*} The operator ![]() $L_{\xi_{1n}}:\mathcal{F}(E)\otimes H \to \mathcal{F}(E)\otimes H$ is defined by
$L_{\xi_{1n}}:\mathcal{F}(E)\otimes H \to \mathcal{F}(E)\otimes H$ is defined by  $L_{\xi_{1n}}(\eta^{(\alpha)} \otimes h) = \xi_{1n} \otimes \eta^{(\alpha)} \otimes h$. Following this, for each
$L_{\xi_{1n}}(\eta^{(\alpha)} \otimes h) = \xi_{1n} \otimes \eta^{(\alpha)} \otimes h$. Following this, for each ![]() $i=2,\ldots,n-1$, we define
$i=2,\ldots,n-1$, we define ![]() $\tilde{L}_i :E_i \otimes\mathcal{F}(E)\otimes H\to \mathcal{F}(E)\otimes H$ by
$\tilde{L}_i :E_i \otimes\mathcal{F}(E)\otimes H\to \mathcal{F}(E)\otimes H$ by
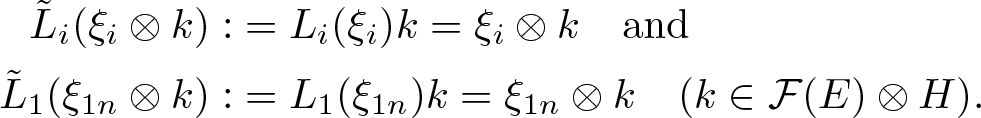 \begin{align}
\tilde{L}_i(\xi_i\otimes k):& =L_i(\xi_i)k=\xi_i \otimes k\quad \text{and}\nonumber\\
\tilde{L}_1(\xi_{1n} \otimes k):& = L_1(\xi_{1n})k =\xi_{1n} \otimes k \quad (k\in \mathcal{F}(E)\otimes H).
\end{align}
\begin{align}
\tilde{L}_i(\xi_i\otimes k):& =L_i(\xi_i)k=\xi_i \otimes k\quad \text{and}\nonumber\\
\tilde{L}_1(\xi_{1n} \otimes k):& = L_1(\xi_{1n})k =\xi_{1n} \otimes k \quad (k\in \mathcal{F}(E)\otimes H).
\end{align} For the above-defined ![]() $(n-1)$-tuple
$(n-1)$-tuple  $\tilde{\hat{T}}_{1n}=\big(\tilde{T}_1(I_1\otimes \tilde{T}_n),\tilde{T_2},\ldots,\tilde{T}_{n-1}\big)$, we consider a dilation map
$\tilde{\hat{T}}_{1n}=\big(\tilde{T}_1(I_1\otimes \tilde{T}_n),\tilde{T_2},\ldots,\tilde{T}_{n-1}\big)$, we consider a dilation map ![]() $\Pi_{1n}:H\to \mathcal{F}(E)\otimes H$ that is defined by
$\Pi_{1n}:H\to \mathcal{F}(E)\otimes H$ that is defined by
 \begin{align}
\Pi_{1n} h:& = \bigoplus_{\alpha \in \mathbb Z_+^{n-1}} (I_{E^{\alpha}}\otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h = D_{\hat{T}_{1n}}h\oplus(I_{E_{1n}}\otimes D_{\hat{T}_{1n}})(\tilde{T}_{1n})^*h\oplus\nonumber\\
& quad \times(I_{E_2}\otimes D_{\hat{T}_{1n}})(\tilde{T}_2)^*h\oplus\cdots ,
\end{align}
\begin{align}
\Pi_{1n} h:& = \bigoplus_{\alpha \in \mathbb Z_+^{n-1}} (I_{E^{\alpha}}\otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h = D_{\hat{T}_{1n}}h\oplus(I_{E_{1n}}\otimes D_{\hat{T}_{1n}})(\tilde{T}_{1n})^*h\oplus\nonumber\\
& quad \times(I_{E_2}\otimes D_{\hat{T}_{1n}})(\tilde{T}_2)^*h\oplus\cdots ,
\end{align} where for  $\alpha = (\alpha_1,\ldots,\alpha_{n-1}) \in \mathbb Z_+^{n-1}$,
$\alpha = (\alpha_1,\ldots,\alpha_{n-1}) \in \mathbb Z_+^{n-1}$,  $E^{\alpha}= E_{1n}^{\otimes \alpha_1} \otimes \cdots \otimes E_{n-1}^{\otimes \alpha_{n-1}}$ and
$E^{\alpha}= E_{1n}^{\otimes \alpha_1} \otimes \cdots \otimes E_{n-1}^{\otimes \alpha_{n-1}}$ and  $\tilde{T}_{1n}^{(\alpha)} = \tilde{T}_{1n}^{\alpha_1} \tilde{T}_2^{\alpha_2} \cdots \tilde{T}_{n-1}^{\alpha_{n-1} - 1} $.
$\tilde{T}_{1n}^{(\alpha)} = \tilde{T}_{1n}^{\alpha_1} \tilde{T}_2^{\alpha_2} \cdots \tilde{T}_{n-1}^{\alpha_{n-1} - 1} $.
Remark 3.10. Note that this is the same map as in proposition 3.1 and in corollary 3.2 but for the product system ![]() $(M, E_{1n},E_2, \ldots, E_{n-1})$ and the tuple
$(M, E_{1n},E_2, \ldots, E_{n-1})$ and the tuple  $\tilde{\hat{T}}_{1n}=(\tilde{T}_1(I_1\otimes \tilde{T}_n),\tilde{T}_2,\ldots, \tilde{T}_{n-1})$.
$\tilde{\hat{T}}_{1n}=(\tilde{T}_1(I_1\otimes \tilde{T}_n),\tilde{T}_2,\ldots, \tilde{T}_{n-1})$.
Now, we are ready to prove a dilation result for the ![]() $(n-1)$-tuple
$(n-1)$-tuple  $\tilde{\hat{T}}_{1n}$.
$\tilde{\hat{T}}_{1n}$.
Proposition 3.11. Let ![]() $\hat{T}_n$ be a pure
$\hat{T}_n$ be a pure ![]() $(n-1)$-tuple. Then, the above-defined map
$(n-1)$-tuple. Then, the above-defined map ![]() $\Pi_{1n}$ is an isometry and
$\Pi_{1n}$ is an isometry and
(i)
 $(I_{1n}\otimes \Pi_{1n})\big(\tilde{T}_{1n}\big)^*=(\tilde{L}_1)^*\Pi_{1n}$.
$(I_{1n}\otimes \Pi_{1n})\big(\tilde{T}_{1n}\big)^*=(\tilde{L}_1)^*\Pi_{1n}$.(ii)
 $(I_i\otimes \Pi_{1n})(\tilde{T}_i)^*=(\tilde{L}_i)^*\Pi_{1n}$ for all
$(I_i\otimes \Pi_{1n})(\tilde{T}_i)^*=(\tilde{L}_i)^*\Pi_{1n}$ for all  $i=2,\ldots, n-1$.
$i=2,\ldots, n-1$.
Proof. The fact that ![]() $\Pi_{1n}$ is an isometry follows from corollary 3.2 (see the remark above). Let
$\Pi_{1n}$ is an isometry follows from corollary 3.2 (see the remark above). Let ![]() $\xi_{1n}\in E_{1n},\eta^{(\beta)}\in E^{\beta}$ and
$\xi_{1n}\in E_{1n},\eta^{(\beta)}\in E^{\beta}$ and ![]() $h\in H$. Then, we
$h\in H$. Then, we
 \begin{align*}
&\langle(\tilde{L}_1)^*\Pi_{1n} h, \xi_{1n} \otimes\eta^{(\beta)}\otimes h \rangle \\
&\quad = \langle\Pi_{1n} h, \tilde{L}_1(\xi_{1n} \otimes \eta^{(\beta)}\otimes h) \rangle \\
&\quad =\Big\langle \bigoplus_{\alpha \in \mathbb Z_+^{n-1}} (I_{E^{\alpha}}\otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h, \xi_{1n} \otimes\eta^{(\beta)}\otimes h\Big\rangle\\
& = \Big\langle (I_{E^{\beta}} \otimes I_{1n} \otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta + e_1)}h, \xi_{1n} \\quad times\eta^{(\beta)}\otimes h\Big\rangle\\
&\quad = \Big\langle\Big[I_{1n} \otimes(I_{E^{\beta}} \otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}\Big](\tilde{T}_{1n})^*h, \xi_{1n} \otimes\eta^{(\beta)}\otimes h\Big\rangle \\
& \quad =\langle (I_{1n}\otimes \Pi_{1n}) (\tilde{T}_{1n})^*, \xi_{1n} \otimes \eta^{(\beta)} \otimes h \rangle .
\end{align*}
\begin{align*}
&\langle(\tilde{L}_1)^*\Pi_{1n} h, \xi_{1n} \otimes\eta^{(\beta)}\otimes h \rangle \\
&\quad = \langle\Pi_{1n} h, \tilde{L}_1(\xi_{1n} \otimes \eta^{(\beta)}\otimes h) \rangle \\
&\quad =\Big\langle \bigoplus_{\alpha \in \mathbb Z_+^{n-1}} (I_{E^{\alpha}}\otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h, \xi_{1n} \otimes\eta^{(\beta)}\otimes h\Big\rangle\\
& = \Big\langle (I_{E^{\beta}} \otimes I_{1n} \otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta + e_1)}h, \xi_{1n} \\quad times\eta^{(\beta)}\otimes h\Big\rangle\\
&\quad = \Big\langle\Big[I_{1n} \otimes(I_{E^{\beta}} \otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}\Big](\tilde{T}_{1n})^*h, \xi_{1n} \otimes\eta^{(\beta)}\otimes h\Big\rangle \\
& \quad =\langle (I_{1n}\otimes \Pi_{1n}) (\tilde{T}_{1n})^*, \xi_{1n} \otimes \eta^{(\beta)} \otimes h \rangle .
\end{align*} On the other hand, for each ![]() $i=2,\ldots,n-1$, take
$i=2,\ldots,n-1$, take ![]() $\xi_i\in E_i,\eta^{(\beta)}\in E^{\beta}$ and
$\xi_i\in E_i,\eta^{(\beta)}\in E^{\beta}$ and ![]() $h\in H$. Then, we have
$h\in H$. Then, we have
 \begin{align*}
&\langle(\tilde{L}_i)^*\Pi_{1n} h, \xi_i \otimes\eta^{(\beta)}\otimes h \rangle \\
& \quad = \langle\Pi_{1n} h, \tilde{L}_i(\xi_i \otimes \eta^{(\beta)}\otimes h) \rangle \\
& \quad =\Big\langle \bigoplus_{\alpha \in \mathbb Z_+^{n-1}} (I_{E^{\alpha}}\otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h, \xi_i \otimes\eta^{(\beta)}\otimes h\Big\rangle\\
& \quad = \Big\langle (I_{E^{(\beta+e_i)}} \otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta + e_i)}h, \xi_i \otimes\eta^{(\beta)}\otimes h\Big\rangle\\
& \quad = \Big\langle\Big[I_i \otimes(I_{E^{\beta}} \otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}\Big](\tilde{T}_i)^*h, \xi_i \otimes\eta^{(\beta)}\otimes h\Big\rangle \\
& \quad =\langle (I_{i}\otimes \Pi_{1n}) (\tilde{T}_i)^*, \xi_i \otimes \eta^{(\beta)} \otimes h \rangle .
\end{align*}
\begin{align*}
&\langle(\tilde{L}_i)^*\Pi_{1n} h, \xi_i \otimes\eta^{(\beta)}\otimes h \rangle \\
& \quad = \langle\Pi_{1n} h, \tilde{L}_i(\xi_i \otimes \eta^{(\beta)}\otimes h) \rangle \\
& \quad =\Big\langle \bigoplus_{\alpha \in \mathbb Z_+^{n-1}} (I_{E^{\alpha}}\otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h, \xi_i \otimes\eta^{(\beta)}\otimes h\Big\rangle\\
& \quad = \Big\langle (I_{E^{(\beta+e_i)}} \otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta + e_i)}h, \xi_i \otimes\eta^{(\beta)}\otimes h\Big\rangle\\
& \quad = \Big\langle\Big[I_i \otimes(I_{E^{\beta}} \otimes D_{\hat{T}_{1n}})\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}\Big](\tilde{T}_i)^*h, \xi_i \otimes\eta^{(\beta)}\otimes h\Big\rangle \\
& \quad =\langle (I_{i}\otimes \Pi_{1n}) (\tilde{T}_i)^*, \xi_i \otimes \eta^{(\beta)} \otimes h \rangle .
\end{align*} Recall that  $V:\mathcal{D}_{\hat{T}_{1n}}\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 =\mathcal{D}$ is an isometry such that
$V:\mathcal{D}_{\hat{T}_{1n}}\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 =\mathcal{D}$ is an isometry such that
 \begin{equation*}V(D_{\hat{T}_{1n}}h)=D_{\hat{T}_n} h \oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}.\end{equation*}
\begin{equation*}V(D_{\hat{T}_{1n}}h)=D_{\hat{T}_n} h \oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}.\end{equation*}We now define the map
by
 \begin{equation*}\Pi_{1n,V}h=(I_{\mathcal{F}(E)}\otimes V)\Pi_{1n} h= \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}\big(I_{E^{\alpha}}\otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h.\end{equation*}
\begin{equation*}\Pi_{1n,V}h=(I_{\mathcal{F}(E)}\otimes V)\Pi_{1n} h= \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}\big(I_{E^{\alpha}}\otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h.\end{equation*} Since both ![]() $\Pi_{1n}$ and V are isometries, so is
$\Pi_{1n}$ and V are isometries, so is ![]() $\Pi_{1n,V}$. Therefore, we have the following dilation result, which basically replaces dilation space with some other Fock space where the coefficient space is
$\Pi_{1n,V}$. Therefore, we have the following dilation result, which basically replaces dilation space with some other Fock space where the coefficient space is ![]() $\mathcal{D}$ instead of
$\mathcal{D}$ instead of  $\mathcal{D}_{\hat{T}_{1n}}$.
$\mathcal{D}_{\hat{T}_{1n}}$.
Proposition 3.12. Let ![]() $\hat{T}_n$ be a pure
$\hat{T}_n$ be a pure ![]() $(n-1)$-tuple and the map
$(n-1)$-tuple and the map ![]() $\Pi_{1n,V}$ as above. Then,
$\Pi_{1n,V}$ as above. Then,
(i)
 $(I_{1n}\otimes \Pi_{1n,V})\big(\tilde{T}_{1n}\big)^*=(\tilde{L}_1)^*\Pi_{1n,V}$.
$(I_{1n}\otimes \Pi_{1n,V})\big(\tilde{T}_{1n}\big)^*=(\tilde{L}_1)^*\Pi_{1n,V}$.(ii)
 $(I_i\otimes \Pi_{1n,V})(\tilde{T}_i)^*=(\tilde{L}_i)^*\Pi_{1n,V}$ for all
$(I_i\otimes \Pi_{1n,V})(\tilde{T}_i)^*=(\tilde{L}_i)^*\Pi_{1n,V}$ for all  $i=2,\ldots, n-1$.
$i=2,\ldots, n-1$.
Proof. To prove
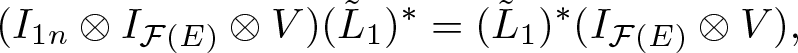 \begin{equation} (I_{1n}\otimes I_{\mathcal{F}(E)}\otimes V)(\tilde{L}_1)^*=(\tilde{L}_1)^*(I_{\mathcal{F}(E)}\otimes V),
\end{equation}
\begin{equation} (I_{1n}\otimes I_{\mathcal{F}(E)}\otimes V)(\tilde{L}_1)^*=(\tilde{L}_1)^*(I_{\mathcal{F}(E)}\otimes V),
\end{equation} note that ![]() $(\tilde{L}_1)^*$ (on the left-hand side) is the inclusion of
$(\tilde{L}_1)^*$ (on the left-hand side) is the inclusion of  $E_{1n}\otimes \mathcal{F}(E) \otimes \mathcal{D}_{\hat{T}_{1n}}$ in
$E_{1n}\otimes \mathcal{F}(E) \otimes \mathcal{D}_{\hat{T}_{1n}}$ in  $\mathcal{F}(E) \otimes \mathcal{D}_{\hat{T}_{1n}},$ while
$\mathcal{F}(E) \otimes \mathcal{D}_{\hat{T}_{1n}},$ while ![]() $(\tilde{L}_1)^*$ (on the right-hand side) is the inclusion of
$(\tilde{L}_1)^*$ (on the right-hand side) is the inclusion of ![]() $E_{1n}\otimes \mathcal{F}(E) \otimes \mathcal{D}$ in
$E_{1n}\otimes \mathcal{F}(E) \otimes \mathcal{D}$ in ![]() $\mathcal{F}(E) \otimes \mathcal{D}$. Thus, for all
$\mathcal{F}(E) \otimes \mathcal{D}$. Thus, for all  $h\in \mathcal{D}_{\hat{T}_{1n}}$,
$h\in \mathcal{D}_{\hat{T}_{1n}}$, ![]() $ \xi_{1n} \in E_{1n}$, and
$ \xi_{1n} \in E_{1n}$, and ![]() $\eta^{(\beta)}\in E^{\beta}$,
$\eta^{(\beta)}\in E^{\beta}$,
 \begin{equation*}(I_{1n}\otimes I_{\mathcal{F}(E)}\otimes V)(\tilde{L}_1)^*(\xi_{1n}\otimes \eta^{(\beta)}\otimes h)=\xi_{1n}\otimes \eta^{(\beta)}\otimes Vh=(\xi_{1n}\otimes \eta^{(\beta)})\otimes Vh\end{equation*}
\begin{equation*}(I_{1n}\otimes I_{\mathcal{F}(E)}\otimes V)(\tilde{L}_1)^*(\xi_{1n}\otimes \eta^{(\beta)}\otimes h)=\xi_{1n}\otimes \eta^{(\beta)}\otimes Vh=(\xi_{1n}\otimes \eta^{(\beta)})\otimes Vh\end{equation*} \begin{equation*}=(\tilde{L}_1)^*(I_{\mathcal{F}(E)}\otimes V)(\xi_{1n}\otimes \eta^{(\beta)}\otimes h),\end{equation*}
\begin{equation*}=(\tilde{L}_1)^*(I_{\mathcal{F}(E)}\otimes V)(\xi_{1n}\otimes \eta^{(\beta)}\otimes h),\end{equation*}proving (3.21). Using this,
 \begin{align*}
(I_{1n}\otimes \Pi_{1n,V})\big(\tilde{T}_{1n}\big)^*&=\big(I_{1n}\otimes (I_{\mathcal{F}(E)}\otimes V)\Pi_{1n}\big)\big(\tilde{T}_{1n}\big)^*\\
&=(I_{1n}\otimes I_{\mathcal{F}(E)}\otimes V)(I_{1n}\otimes \Pi_{1n} )\big(\tilde{T}_{1n}\big)^*\\
&=(I_{1n}\otimes I_{\mathcal{F}(E)}\otimes V)(\tilde{L}_1)^*\Pi_{1n}\qquad(\text{by (a) of proposition 3.11})\\
&=(\tilde{L}_1)^*(I_{\mathcal{F}(E)}\otimes V)\Pi_{1n}\qquad(\text{by }34)\\
&=(\tilde{L}_1)^*\Pi_{1n,V}.
\end{align*}
\begin{align*}
(I_{1n}\otimes \Pi_{1n,V})\big(\tilde{T}_{1n}\big)^*&=\big(I_{1n}\otimes (I_{\mathcal{F}(E)}\otimes V)\Pi_{1n}\big)\big(\tilde{T}_{1n}\big)^*\\
&=(I_{1n}\otimes I_{\mathcal{F}(E)}\otimes V)(I_{1n}\otimes \Pi_{1n} )\big(\tilde{T}_{1n}\big)^*\\
&=(I_{1n}\otimes I_{\mathcal{F}(E)}\otimes V)(\tilde{L}_1)^*\Pi_{1n}\qquad(\text{by (a) of proposition 3.11})\\
&=(\tilde{L}_1)^*(I_{\mathcal{F}(E)}\otimes V)\Pi_{1n}\qquad(\text{by }34)\\
&=(\tilde{L}_1)^*\Pi_{1n,V}.
\end{align*}This proves (i). Proof of item (ii) is similar.
Below, we develop an identity (namely the identity (3.22)) related to the block entries of the above-defined unitary U 1, which turns out to be a key identity to establish a dilation for the c.c. representations in our class ![]() $\mathcal{T}_{1,n}^n(\sigma, M, E_1,\ldots,E_n , H)$.
$\mathcal{T}_{1,n}^n(\sigma, M, E_1,\ldots,E_n , H)$.
Let  $$U_1=\left(\begin{array}{cc} A & B \\ C & 0 \end{array}\right)$$, where
$$U_1=\left(\begin{array}{cc} A & B \\ C & 0 \end{array}\right)$$, where ![]() $A=(I_1\otimes U)P_1$,
$A=(I_1\otimes U)P_1$, ![]() $B=(I_1\otimes U)j_2'$, and
$B=(I_1\otimes U)j_2'$, and ![]() $C=i_2^*$. So, by lemma 3.9,
$C=i_2^*$. So, by lemma 3.9,
 \begin{align*}& \left(\begin{array}{cc} A & B \\ C & 0 \end{array}\right) \left(\begin{array}{c} VD_{\hat{T}_{1n}}h \\ (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h \oplus 0_{E_{1n}\otimes \mathcal{E}_1}\end{array}\right)\\
& \quad =\left(\begin{array}{c} (I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h\\ D_{\hat{T}_n} h\oplus 0_{\mathcal{E}_1}\end{array}\right).\end{align*}
\begin{align*}& \left(\begin{array}{cc} A & B \\ C & 0 \end{array}\right) \left(\begin{array}{c} VD_{\hat{T}_{1n}}h \\ (I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h \oplus 0_{E_{1n}\otimes \mathcal{E}_1}\end{array}\right)\\
& \quad =\left(\begin{array}{c} (I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h\\ D_{\hat{T}_n} h\oplus 0_{\mathcal{E}_1}\end{array}\right).\end{align*}This implies,
 \begin{equation*}
AVD_{\hat{T}_{1n}}h+B\big[(I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h \oplus 0_{E_{1n}\otimes \mathcal{E}_1}\big]=(I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h
\end{equation*}
\begin{equation*}
AVD_{\hat{T}_{1n}}h+B\big[(I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h \oplus 0_{E_{1n}\otimes \mathcal{E}_1}\big]=(I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h
\end{equation*}and
 \begin{equation*}
CVD_{\hat{T}_{1n}}h=D_{\hat{T}_n} h\oplus 0_{\mathcal{E}_1}.
\end{equation*}
\begin{equation*}
CVD_{\hat{T}_{1n}}h=D_{\hat{T}_n} h\oplus 0_{\mathcal{E}_1}.
\end{equation*}The above two together imply
 \begin{align*}
&AVD_{\hat{T}_{1n}}h+B\big[(I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h \oplus 0_{E_{1n}\otimes \mathcal{E}_1}\big]\\
=&AVD_{\hat{T}_{1n}}h+B\big[\big(I_{1n}\otimes (D_{\hat{T}_n} \oplus \boldsymbol{0}_{\mathcal{E}_1})\big)(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\big]\\
=&AVD_{\hat{T}_{1n}}h+B\big[\big(I_{1n}\otimes CVD_{\hat{T}_{1n}}\big)(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\big]\\
=&(I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h.
\end{align*}
\begin{align*}
&AVD_{\hat{T}_{1n}}h+B\big[(I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h \oplus 0_{E_{1n}\otimes \mathcal{E}_1}\big]\\
=&AVD_{\hat{T}_{1n}}h+B\big[\big(I_{1n}\otimes (D_{\hat{T}_n} \oplus \boldsymbol{0}_{\mathcal{E}_1})\big)(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\big]\\
=&AVD_{\hat{T}_{1n}}h+B\big[\big(I_{1n}\otimes CVD_{\hat{T}_{1n}}\big)(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h\big]\\
=&(I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h.
\end{align*}Thus, we have the identity,
 \begin{equation}
AVD_{\hat{T}_{1n}}h+B\big[(I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h \oplus 0_{E_{1n}\otimes \mathcal{E}_1}\big]=(I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h.
\end{equation}
\begin{equation}
AVD_{\hat{T}_{1n}}h+B\big[(I_{1n}\otimes D_{\hat{T}_n} )(I_1\otimes (\tilde{T_n})^*)(\tilde{T}_1)^*h \oplus 0_{E_{1n}\otimes \mathcal{E}_1}\big]=(I_1\otimes VD_{\hat{T}_{1n}})(\tilde{T}_1)^*h.
\end{equation} Define an operator ![]() $\tau_{U_1^*}$, which has a transfer function-type representation corresponding to the unitary
$\tau_{U_1^*}$, which has a transfer function-type representation corresponding to the unitary ![]() $U_1^*$, by
$U_1^*$, by
 \begin{equation} \tau_{U_1^*}:=I_{\mathcal{F}(E)}\otimes \big(A^*+[I_{1n}\otimes C^*] B^*\big).\end{equation}
\begin{equation} \tau_{U_1^*}:=I_{\mathcal{F}(E)}\otimes \big(A^*+[I_{1n}\otimes C^*] B^*\big).\end{equation}More explicitly,
 \begin{equation*} \tau_{U_1^*}=I_{\mathcal{F}(E)}\otimes \big(P_1^*(I_1\otimes U^*)+[I_{1n}\otimes i_2] (j_2')^*(I_1\otimes U^*)\big).\end{equation*}
\begin{equation*} \tau_{U_1^*}=I_{\mathcal{F}(E)}\otimes \big(P_1^*(I_1\otimes U^*)+[I_{1n}\otimes i_2] (j_2')^*(I_1\otimes U^*)\big).\end{equation*}This map will play an important role.
Note that
 \begin{equation}\tau_{U_1^*}:\mathcal{F}(E)\otimes E_1\otimes \mathcal{D} \rightarrow \mathcal{F}(E)\otimes [\mathcal{D} \oplus (E_{1n}\otimes \mathcal{D})]\subseteq \mathcal{F}(E)\otimes \mathcal{D}, \end{equation}
\begin{equation}\tau_{U_1^*}:\mathcal{F}(E)\otimes E_1\otimes \mathcal{D} \rightarrow \mathcal{F}(E)\otimes [\mathcal{D} \oplus (E_{1n}\otimes \mathcal{D})]\subseteq \mathcal{F}(E)\otimes \mathcal{D}, \end{equation} and we view here ![]() $\mathcal{F}(E)\otimes E_{1n}\otimes \mathcal{D}$ as a subspace of
$\mathcal{F}(E)\otimes E_{1n}\otimes \mathcal{D}$ as a subspace of ![]() $\mathcal{F}(E)\otimes \mathcal{D}$.
$\mathcal{F}(E)\otimes \mathcal{D}$.
Proposition 3.13. For the unitary U 1, ![]() $\tau_{U_1^*}$ is a well-defined isometry.
$\tau_{U_1^*}$ is a well-defined isometry.
Proof. To show that ![]() $\tau_{U_1^*}$ is well defined, we need to show that
$\tau_{U_1^*}$ is well defined, we need to show that ![]() $B(I_{1n}\otimes C)$ is well defined. For this, recall that
$B(I_{1n}\otimes C)$ is well defined. For this, recall that ![]() $C=i_2^*$ and, thus,
$C=i_2^*$ and, thus,  $I_{1n}\otimes C=I_{1n}\otimes i_2^*:(E_{1n}\otimes\mathcal{D}_{\hat{T}_n} )\oplus (E_{1n}\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \oplus (E_{1n}\otimes \mathcal{E}_1) \rightarrow (E_{1n}\otimes\mathcal{D}_{\hat{T}_n} ) \oplus (E_{1n}\otimes \mathcal{E}_1) .$ For B, we have
$I_{1n}\otimes C=I_{1n}\otimes i_2^*:(E_{1n}\otimes\mathcal{D}_{\hat{T}_n} )\oplus (E_{1n}\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \oplus (E_{1n}\otimes \mathcal{E}_1) \rightarrow (E_{1n}\otimes\mathcal{D}_{\hat{T}_n} ) \oplus (E_{1n}\otimes \mathcal{E}_1) .$ For B, we have ![]() $B=(I_1\otimes U)j_2'$, which is defined on
$B=(I_1\otimes U)j_2'$, which is defined on ![]() $(E_{1n}\otimes \mathcal{D}_{\hat{T}_n})\oplus (E_{1n}\otimes \mathcal{E}_1)$. Thus,
$(E_{1n}\otimes \mathcal{D}_{\hat{T}_n})\oplus (E_{1n}\otimes \mathcal{E}_1)$. Thus, ![]() $B(I_{1n}\otimes C)$ is well defined. The following computation shows that
$B(I_{1n}\otimes C)$ is well defined. The following computation shows that ![]() $\tau_{U_1^*}$ is indeed an isometry:
$\tau_{U_1^*}$ is indeed an isometry:
 \begin{align*}
\tau_{U_1^*}^*\tau_{U_1^*}& =\Big[I_{\mathcal{F}(E)}\otimes \big(A+B[I_{1n}\otimes C]\big)\Big]\Big[I_{\mathcal{F}(E)}\otimes \big(A^*+[I_{1n}\otimes C^*] B^*\big)\Big]\\
& =\big(I_{\mathcal{F}(E)}\otimes A\big)\big(I_{\mathcal{F}(E)}\otimes A^*\big)+\big(I_{\mathcal{F}(E)}\otimes A\big)\big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*] B^*\big)\\
& \quad + \big(I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes C]\big)\big(I_{\mathcal{F}(E)}\otimes A^*\big)+ \big(I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes C]\big)\\
& \quad \times \big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*] B^*\big).
\end{align*}
\begin{align*}
\tau_{U_1^*}^*\tau_{U_1^*}& =\Big[I_{\mathcal{F}(E)}\otimes \big(A+B[I_{1n}\otimes C]\big)\Big]\Big[I_{\mathcal{F}(E)}\otimes \big(A^*+[I_{1n}\otimes C^*] B^*\big)\Big]\\
& =\big(I_{\mathcal{F}(E)}\otimes A\big)\big(I_{\mathcal{F}(E)}\otimes A^*\big)+\big(I_{\mathcal{F}(E)}\otimes A\big)\big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*] B^*\big)\\
& \quad + \big(I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes C]\big)\big(I_{\mathcal{F}(E)}\otimes A^*\big)+ \big(I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes C]\big)\\
& \quad \times \big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*] B^*\big).
\end{align*} The first term and the last term of the above sum are equal to ![]() $I_{\mathcal{F}(E)}\otimes AA^*$ and
$I_{\mathcal{F}(E)}\otimes AA^*$ and ![]() $I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes CC^*]B^*$, respectively. Recall now that
$I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes CC^*]B^*$, respectively. Recall now that
 \begin{align*}
B^*:& \,E_1\otimes \mathcal{D} \to E_{1n}\otimes \mathcal{D}^{'}\\
C^*:& \,\mathcal{D}^{'}\to \mathcal{D}\\
A:& \,\mathcal{D} \to E_1\otimes \mathcal{D}.
\end{align*}
\begin{align*}
B^*:& \,E_1\otimes \mathcal{D} \to E_{1n}\otimes \mathcal{D}^{'}\\
C^*:& \,\mathcal{D}^{'}\to \mathcal{D}\\
A:& \,\mathcal{D} \to E_1\otimes \mathcal{D}.
\end{align*} It follows that the range of ![]() $I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*] B^*$ is contained in
$I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*] B^*$ is contained in ![]() $\mathcal{F}(E)\otimes E_{1n}\otimes \mathcal{D} (\subseteq \mathcal{F}(E)\otimes \mathcal{D})$. On this range,
$\mathcal{F}(E)\otimes E_{1n}\otimes \mathcal{D} (\subseteq \mathcal{F}(E)\otimes \mathcal{D})$. On this range, ![]() $I_{\mathcal{F}(E)}\otimes A$ equals
$I_{\mathcal{F}(E)}\otimes A$ equals ![]() $I_{\mathcal{F}(E)}\otimes I_{1n}\otimes A$ and, thus, the third term is
$I_{\mathcal{F}(E)}\otimes I_{1n}\otimes A$ and, thus, the third term is ![]() $I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes AC^*]B^*$ and the fourth term is its adjoint.
$I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes AC^*]B^*$ and the fourth term is its adjoint.
Hence,
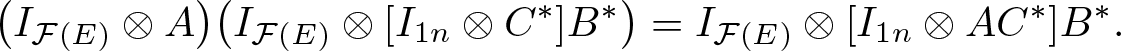 \begin{equation*}\big(I_{\mathcal{F}(E)}\otimes A\big)\big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*] B^*\big)=I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes AC^*] B^*.\end{equation*}
\begin{equation*}\big(I_{\mathcal{F}(E)}\otimes A\big)\big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*] B^*\big)=I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes AC^*] B^*.\end{equation*}Similarly,
 \begin{equation*}
\big(I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes C]\big)\big(I_{\mathcal{F}(E)}\otimes A^*\big)=I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes CA^*].
\end{equation*}
\begin{equation*}
\big(I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes C]\big)\big(I_{\mathcal{F}(E)}\otimes A^*\big)=I_{\mathcal{F}(E)}\otimes B[I_{1n}\otimes CA^*].
\end{equation*}Therefore,
 \begin{equation*}
\tau_{U_1^*}^*\tau_{U_1^*}=I_{\mathcal{F}(E)}\otimes \big(AA^*+[I_{1n}\otimes AC^*] B^*+B[I_{1n}\otimes CA^*]+B[I_{1n}\otimes CC^*]B^*\big).
\end{equation*}
\begin{equation*}
\tau_{U_1^*}^*\tau_{U_1^*}=I_{\mathcal{F}(E)}\otimes \big(AA^*+[I_{1n}\otimes AC^*] B^*+B[I_{1n}\otimes CA^*]+B[I_{1n}\otimes CC^*]B^*\big).
\end{equation*}The fact that U 1 is a unitary implies
and hence,
 \begin{equation*}
\tau_{U_1^*}^*\tau_{U_1^*}=I_{\mathcal{F}(E)\otimes E_1\otimes \mathcal{D}}.
\end{equation*}
\begin{equation*}
\tau_{U_1^*}^*\tau_{U_1^*}=I_{\mathcal{F}(E)\otimes E_1\otimes \mathcal{D}}.
\end{equation*}Now, using the identity (3.22), we prove the following dilation result.
Theorem 3.14  $(I_1\otimes\Pi_{1n,V})(\tilde{T}_1)^*=\tau_{U_1^*}^*\Pi_{1n,V}$.
$(I_1\otimes\Pi_{1n,V})(\tilde{T}_1)^*=\tau_{U_1^*}^*\Pi_{1n,V}$.
Proof. For ![]() $h\in H$,
$h\in H$, ![]() $\eta^{(\beta)}\in E^{\beta}$, and
$\eta^{(\beta)}\in E^{\beta}$, and  $k \in E_1\otimes \big(D_{\hat{T}_n}\oplus (E_1\otimes D_{\hat{T}_1})\oplus\mathcal{E}_1 \big)$, using the definition of
$k \in E_1\otimes \big(D_{\hat{T}_n}\oplus (E_1\otimes D_{\hat{T}_1})\oplus\mathcal{E}_1 \big)$, using the definition of ![]() $\tau_{U_1^*}$, dilation map
$\tau_{U_1^*}$, dilation map ![]() $\Pi_{1n,V}$, and the decomposition
$\Pi_{1n,V}$, and the decomposition  $\mathcal{F}(E)=\bigoplus_{\alpha\in\mathbb{Z}_+^{n-1}}E^{\alpha}$, we have
$\mathcal{F}(E)=\bigoplus_{\alpha\in\mathbb{Z}_+^{n-1}}E^{\alpha}$, we have
 \begin{align*}
&\langle\tau_{U_1^*}^*\Pi_{1n,V}h,\eta^{(\beta)}\otimes k\rangle\\
& \quad = \Big\langle \Pi_{1n,V}h,
\big[ I_{\mathcal{F}(E)}\otimes A^*+\big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*]\big)(I_{\mathcal{F}(E)}\otimes B^*)\big]\big(\eta^{(\beta)}\otimes k\big)\Big\rangle\\
&\quad =\Big\langle \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big( I_{E^{\alpha}} \otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h, \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big( I_{E^{\alpha}}\otimes A^*\big)\Big)(\eta^{(\beta)}\otimes k) \Big \rangle\\
&\qquad + \Big\langle \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big( I_{E^{\alpha}} \otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h, \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}
\big( I_{E^{\alpha}} \otimes[I_{1n}\otimes C^*]\big)\Big)\\
& \qquad \times \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}
\big( I_{E^{\alpha}} \otimes B^*\big)\Big)(\eta^{(\beta)}\otimes k) \Big \rangle\\
&\quad = \Big\langle\big( I_{E^{\beta}} \otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \big( I_{E^{\beta}} \otimes A^*\big) (\eta^{(\beta)}\otimes k) \Big \rangle \\
&\qquad + \Big\langle \bigoplus_{\alpha= (0,\alpha_2,\ldots,\alpha_{n-1}) \in \mathbb{Z}_+^{n-1}} \big(I_{E^{\alpha}} \otimes VD_{\hat{T}_{1n}} \big) \left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h\\
& \qquad + \quad
I_{1n} \otimes \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big(I_{E^{\alpha}}\otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha + e_1)}h,\\
&\qquad \times \Big(I_{1n}\otimes\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big( I_{E^{\alpha}} \otimes C^*\big)\Big) \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}
\big( I_{E^{\alpha}}\otimes B^*\big)\Big)
(\eta^{(\beta)}\otimes k) \Big \rangle\\
&\quad = \langle\big( I_{E^{\beta}} \otimes AVD_{\hat{T}_{1n}}\big) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k\big \rangle\\
&\qquad + \Big\langle
I_{1n} \otimes \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big(I_{E^{\alpha}} \otimes CVD_{\hat{T}_{1n}}\big) \left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha + e_1)}h,\\
& \qquad \times \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}\big( I_{E^{\alpha}} \otimes B^*\big)\Big)(\eta^{(\beta)} \otimes k) \Big \rangle\\
&\quad = \Big\langle\big( I_{E^{\beta}} \otimes AVD_{\hat{T}_{1n}}\big) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k\Big \rangle\\
&\qquad+ \big\langle I_{1n}\otimes\big(I_{E^{\beta}} \otimes CVD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta + e_1)}, \big( I_{E^{\beta}} \otimes B^*\big)(\eta^{(\beta)}\otimes k)\Big\rangle \\
&\quad = \Big\langle\big( I_{E^{\beta}} \otimes AVD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \Big \rangle \\
&\qquad + \Big\langle I_{E^{\beta}} \otimes \big[\big(I_{1n} \otimes CVD_{\hat{T}_{1n}}\big)(\tilde{T}_{1n})^*\big]\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \big( I_{E^{\beta}} \otimes B^*\big)(\eta^{(\beta)}\otimes k) \Big\rangle \\
&\quad = \Big\langle(I_{E^{\beta}} \otimes AVD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h + \Big[I_{E^{\beta}} \otimes B(I_{1n} \otimes CVD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^*\Big]\\
& \qquad \times \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \Big\rangle.
\end{align*}
\begin{align*}
&\langle\tau_{U_1^*}^*\Pi_{1n,V}h,\eta^{(\beta)}\otimes k\rangle\\
& \quad = \Big\langle \Pi_{1n,V}h,
\big[ I_{\mathcal{F}(E)}\otimes A^*+\big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes C^*]\big)(I_{\mathcal{F}(E)}\otimes B^*)\big]\big(\eta^{(\beta)}\otimes k\big)\Big\rangle\\
&\quad =\Big\langle \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big( I_{E^{\alpha}} \otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h, \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big( I_{E^{\alpha}}\otimes A^*\big)\Big)(\eta^{(\beta)}\otimes k) \Big \rangle\\
&\qquad + \Big\langle \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big( I_{E^{\alpha}} \otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h, \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}
\big( I_{E^{\alpha}} \otimes[I_{1n}\otimes C^*]\big)\Big)\\
& \qquad \times \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}
\big( I_{E^{\alpha}} \otimes B^*\big)\Big)(\eta^{(\beta)}\otimes k) \Big \rangle\\
&\quad = \Big\langle\big( I_{E^{\beta}} \otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \big( I_{E^{\beta}} \otimes A^*\big) (\eta^{(\beta)}\otimes k) \Big \rangle \\
&\qquad + \Big\langle \bigoplus_{\alpha= (0,\alpha_2,\ldots,\alpha_{n-1}) \in \mathbb{Z}_+^{n-1}} \big(I_{E^{\alpha}} \otimes VD_{\hat{T}_{1n}} \big) \left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha)}h\\
& \qquad + \quad
I_{1n} \otimes \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big(I_{E^{\alpha}}\otimes VD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha + e_1)}h,\\
&\qquad \times \Big(I_{1n}\otimes\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big( I_{E^{\alpha}} \otimes C^*\big)\Big) \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}
\big( I_{E^{\alpha}}\otimes B^*\big)\Big)
(\eta^{(\beta)}\otimes k) \Big \rangle\\
&\quad = \langle\big( I_{E^{\beta}} \otimes AVD_{\hat{T}_{1n}}\big) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k\big \rangle\\
&\qquad + \Big\langle
I_{1n} \otimes \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} \big(I_{E^{\alpha}} \otimes CVD_{\hat{T}_{1n}}\big) \left(\tilde{\hat{T}}_{1n}\right)^{*(\alpha + e_1)}h,\\
& \qquad \times \Big(\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}}\big( I_{E^{\alpha}} \otimes B^*\big)\Big)(\eta^{(\beta)} \otimes k) \Big \rangle\\
&\quad = \Big\langle\big( I_{E^{\beta}} \otimes AVD_{\hat{T}_{1n}}\big) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k\Big \rangle\\
&\qquad+ \big\langle I_{1n}\otimes\big(I_{E^{\beta}} \otimes CVD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta + e_1)}, \big( I_{E^{\beta}} \otimes B^*\big)(\eta^{(\beta)}\otimes k)\Big\rangle \\
&\quad = \Big\langle\big( I_{E^{\beta}} \otimes AVD_{\hat{T}_{1n}}\big)\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \Big \rangle \\
&\qquad + \Big\langle I_{E^{\beta}} \otimes \big[\big(I_{1n} \otimes CVD_{\hat{T}_{1n}}\big)(\tilde{T}_{1n})^*\big]\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \big( I_{E^{\beta}} \otimes B^*\big)(\eta^{(\beta)}\otimes k) \Big\rangle \\
&\quad = \Big\langle(I_{E^{\beta}} \otimes AVD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h + \Big[I_{E^{\beta}} \otimes B(I_{1n} \otimes CVD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^*\Big]\\
& \qquad \times \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \Big\rangle.
\end{align*}Now, using the identity (3.22), we conclude
 \begin{align*}
\langle\tau_{U_1^*}^*\Pi_{1n,V}h,\eta^{(\beta)}\otimes k\rangle=&\Big\langle\big[I_{E^{\beta}} \otimes (I_1 \otimes VD_{\hat{T}_{1n}}) (\tilde{T}_1)^* \big] \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \Big\rangle\\
=& \Big\langle\Big[I_1\otimes (I_{E^{\beta}} \otimes VD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}\Big] (\tilde{T}_1)^*h,\eta^{(\beta)} \otimes k \Big\rangle\\
=&\langle(I_1\otimes\Pi_{1n,V})(\tilde{T}_1)^*h,\eta^{(\beta)} \otimes k \rangle.
\end{align*}
\begin{align*}
\langle\tau_{U_1^*}^*\Pi_{1n,V}h,\eta^{(\beta)}\otimes k\rangle=&\Big\langle\big[I_{E^{\beta}} \otimes (I_1 \otimes VD_{\hat{T}_{1n}}) (\tilde{T}_1)^* \big] \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \Big\rangle\\
=& \Big\langle\Big[I_1\otimes (I_{E^{\beta}} \otimes VD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}\Big] (\tilde{T}_1)^*h,\eta^{(\beta)} \otimes k \Big\rangle\\
=&\langle(I_1\otimes\Pi_{1n,V})(\tilde{T}_1)^*h,\eta^{(\beta)} \otimes k \rangle.
\end{align*} Now, we will establish an isometric dilation of Tn using the dilation map ![]() $\Pi_{1n,V}$. As in the case of T 1, we will suitably define a unitary such that a multiplication operator that has transfer function-type representation corresponding to that unitary gives us the required isometric dilation.
$\Pi_{1n,V}$. As in the case of T 1, we will suitably define a unitary such that a multiplication operator that has transfer function-type representation corresponding to that unitary gives us the required isometric dilation.
We already know that the unitary
 \begin{equation*}U: \mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \end{equation*}
\begin{equation*}U: \mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \end{equation*}satisfies
 \begin{equation*}
U(D_{\hat{T}_1} h \oplus (I_n \otimes D_{\hat{T}_n} ) (\tilde{T_n})^*h\oplus 0_{\mathcal{E}_2}) = (D_{\hat{T}_n} h \oplus (I_1 \otimes D_{\hat{T}_1} ) (\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}).
\end{equation*}
\begin{equation*}
U(D_{\hat{T}_1} h \oplus (I_n \otimes D_{\hat{T}_n} ) (\tilde{T_n})^*h\oplus 0_{\mathcal{E}_2}) = (D_{\hat{T}_n} h \oplus (I_1 \otimes D_{\hat{T}_1} ) (\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}).
\end{equation*}So the adjoint operator
 \begin{equation*}U^*: \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1\rightarrow \mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2 \end{equation*}
\begin{equation*}U^*: \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1\rightarrow \mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2 \end{equation*}satisfies
 \begin{equation*} U^*(D_{\hat{T}_n} h \oplus (I_1 \otimes D_{\hat{T}_1} ) (\tilde{T}_1)^*h \oplus 0_{\mathcal{E}_1}) = (D_{\hat{T}_1} h \oplus (I_n \otimes D_{\hat{T}_n} ) (\tilde{T_n})^*h \oplus 0_{\mathcal{E}_2}). \end{equation*}
\begin{equation*} U^*(D_{\hat{T}_n} h \oplus (I_1 \otimes D_{\hat{T}_1} ) (\tilde{T}_1)^*h \oplus 0_{\mathcal{E}_1}) = (D_{\hat{T}_1} h \oplus (I_n \otimes D_{\hat{T}_n} ) (\tilde{T_n})^*h \oplus 0_{\mathcal{E}_2}). \end{equation*}We now need to consider the following operators:
(i) P 2 is the projection
 \begin{equation*}P_2:\mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2 \rightarrow (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2\end{equation*}
\begin{equation*}P_2:\mathcal{D}_{\hat{T}_1} \oplus (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2 \rightarrow (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2\end{equation*}(ii)
 $i_1'$ is the inclusion
$i_1'$ is the inclusion
 \begin{equation*}i_1':(E_n \otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \rightarrow (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_n\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \oplus (E_n \otimes \mathcal{E}_1) .\end{equation*}
\begin{equation*}i_1':(E_n \otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \rightarrow (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_n\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} ) \oplus (E_n \otimes \mathcal{E}_1) .\end{equation*}(iii) i 1 is another inclusion
 \begin{equation*}i_1:\mathcal{D}_{\hat{T}_1} \rightarrow \mathcal{D}_{\hat{T}_1} \oplus (E_n \otimes \mathcal{D}_{\hat{T}_n} ) \oplus \mathcal{E}_2\end{equation*}
\begin{equation*}i_1:\mathcal{D}_{\hat{T}_1} \rightarrow \mathcal{D}_{\hat{T}_1} \oplus (E_n \otimes \mathcal{D}_{\hat{T}_n} ) \oplus \mathcal{E}_2\end{equation*}so that
 $i_1^*$ is the projection
$i_1^*$ is the projection
 \begin{equation*}i_1^*:\mathcal{D}_{\hat{T}_1} \oplus (E_n \otimes \mathcal{D}_{\hat{T}_n} ) \oplus \mathcal{E}_2 \rightarrow \mathcal{D}_{\hat{T}_1} .\end{equation*}
\begin{equation*}i_1^*:\mathcal{D}_{\hat{T}_1} \oplus (E_n \otimes \mathcal{D}_{\hat{T}_n} ) \oplus \mathcal{E}_2 \rightarrow \mathcal{D}_{\hat{T}_1} .\end{equation*}
Recall the map  $V:\mathcal{D}_{\hat{T}_{1n}}\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 $ such that
$V:\mathcal{D}_{\hat{T}_{1n}}\rightarrow \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 $ such that
 \begin{equation*}V(D_{\hat{T}_{1n}}h)=D_{\hat{T}_n} h \oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}.\end{equation*}
\begin{equation*}V(D_{\hat{T}_{1n}}h)=D_{\hat{T}_n} h \oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}.\end{equation*}Let
 \begin{equation}
\mathcal{D}_{1n}=\mathcal{D}_{\hat{T}_n} \oplus (E_1 \otimes \mathcal{D}_{\hat{T}_1} ).
\end{equation}
\begin{equation}
\mathcal{D}_{1n}=\mathcal{D}_{\hat{T}_n} \oplus (E_1 \otimes \mathcal{D}_{\hat{T}_1} ).
\end{equation}With this notation, let
 \begin{equation*}U_n:= \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^* & i_1' \\ i_1^*U^* & 0 \end{array}\right) : \left(\begin{array}{c} \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \\ (E_n\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} )\end{array}\right) \end{equation*}
\begin{equation*}U_n:= \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^* & i_1' \\ i_1^*U^* & 0 \end{array}\right) : \left(\begin{array}{c} \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus \mathcal{E}_1 \\ (E_n\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} )\end{array}\right) \end{equation*} \begin{equation*}\rightarrow \left(\begin{array}{c} (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_n\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} )\oplus ( E_n\otimes \mathcal{E}_1 )\\ \mathcal{D}_{\hat{T}_1} \end{array}\right). \end{equation*}
\begin{equation*}\rightarrow \left(\begin{array}{c} (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_n\otimes E_1 \otimes \mathcal{D}_{\hat{T}_1} )\oplus ( E_n\otimes \mathcal{E}_1 )\\ \mathcal{D}_{\hat{T}_1} \end{array}\right). \end{equation*}So that
 \begin{equation*}U_n= \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^* & i_1' \\ i_1^*U^* & 0 \end{array}\right) : \left(\begin{array}{c} \mathcal{D} \\ E_{1n}\otimes\mathcal{D}_{\hat{T}_1} \end{array}\right) \rightarrow \left(\begin{array}{c} E_n\otimes \mathcal{D}\\\mathcal{D}_{\hat{T}_1} \end{array}\right). \end{equation*}
\begin{equation*}U_n= \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^* & i_1' \\ i_1^*U^* & 0 \end{array}\right) : \left(\begin{array}{c} \mathcal{D} \\ E_{1n}\otimes\mathcal{D}_{\hat{T}_1} \end{array}\right) \rightarrow \left(\begin{array}{c} E_n\otimes \mathcal{D}\\\mathcal{D}_{\hat{T}_1} \end{array}\right). \end{equation*}A straightforward computation shows that Un is unitary.
Lemma 3.15. The operator Un intertwines the representations of M, that is,
 \begin{equation*}U_n(\rho_{\mathcal{D}}(a) \oplus (\varphi_{1n}(a)\otimes I_{\mathcal{D}_{\hat{T}_1}}))=((\varphi_{2}(a)\otimes I_{\mathcal{D}})\oplus \sigma(a)|_{\mathcal{D}_{\hat{T}_1}} )U_n\end{equation*}
\begin{equation*}U_n(\rho_{\mathcal{D}}(a) \oplus (\varphi_{1n}(a)\otimes I_{\mathcal{D}_{\hat{T}_1}}))=((\varphi_{2}(a)\otimes I_{\mathcal{D}})\oplus \sigma(a)|_{\mathcal{D}_{\hat{T}_1}} )U_n\end{equation*} for every ![]() $a\in M$.
$a\in M$.
Proof. We need to prove the following, for every ![]() $a\in M$,
$a\in M$,
(i)
 $(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*\rho_{\mathcal{D}}(a)=(\varphi_2(a)\otimes I_{\mathcal{D}})(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*$.
$(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*\rho_{\mathcal{D}}(a)=(\varphi_2(a)\otimes I_{\mathcal{D}})(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*$.(ii)
 $i_1'(\varphi_{1n}(a)\otimes I_{\mathcal{D}_{\hat{T}_1}})=(\varphi_2(a)\otimes I_{\mathcal{D}})i_1'$
$i_1'(\varphi_{1n}(a)\otimes I_{\mathcal{D}_{\hat{T}_1}})=(\varphi_2(a)\otimes I_{\mathcal{D}})i_1'$(iii)
 $i_1^*U^*\rho_{\mathcal{D}}(a)=\sigma(a)i_1^*U^*$.
$i_1^*U^*\rho_{\mathcal{D}}(a)=\sigma(a)i_1^*U^*$.
We start with (i) and compute, using the intertwining property of ![]() $U^*$ (see proposition 3.7),
$U^*$ (see proposition 3.7),
 \begin{equation*}(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*\rho_{\mathcal{D}}(a)=(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2(\sigma(a)\oplus (\varphi_2(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus \rho_2(a))U^*.\end{equation*}
\begin{equation*}(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*\rho_{\mathcal{D}}(a)=(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2(\sigma(a)\oplus (\varphi_2(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus \rho_2(a))U^*.\end{equation*}Using the definition of P 2, this is equal to
 \begin{equation*}(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)((\varphi_2(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus \rho_2(a))P_2U^*=((\varphi_2(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus(\varphi_2(a)\otimes I_{\mathcal{E}_1})u_2)P_2U^*\end{equation*}
\begin{equation*}(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)((\varphi_2(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus \rho_2(a))P_2U^*=((\varphi_2(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus(\varphi_2(a)\otimes I_{\mathcal{E}_1})u_2)P_2U^*\end{equation*} \begin{equation*}=((\varphi_2(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus(\varphi_2(a)\otimes I_{\mathcal{E}_1}))(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*=(\varphi_2(a)\otimes I_{\mathcal{D}})(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*,\end{equation*}
\begin{equation*}=((\varphi_2(a)\otimes I_{\mathcal{D}_{\hat{T}_n}})\oplus(\varphi_2(a)\otimes I_{\mathcal{E}_1}))(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*=(\varphi_2(a)\otimes I_{\mathcal{D}})(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2)P_2U^*,\end{equation*}proving (i).
Using an analogous argument as in the proof of lemma 3.8 and the intertwining properties of ![]() $U^*$, we can prove (ii) and (iii).
$U^*$, we can prove (ii) and (iii).
Now, we compute the action of the unitary Un on some special type of elements, as in the case of U 1 in lemma 3.9, which will be used in establishing the dilation of Tn.
 \begin{align*}
& U_n\big(VD_{\hat{T}_{1n}}h, (I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h\big) \\
& \quad = U_n\big(D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}, (I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \big) \\
& \quad = \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^* & i_1' \\ i_1^*U^* & 0 \end{array}\right) \left(\begin{array}{cc} D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1} \\ (I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \end{array}\right) \\
& \quad = \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^*\big( D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h \oplus 0_{\mathcal{E}_1}\big)\\
+
i_1' \big( (I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \big) \\
i_1^*U^*\big( D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1} \big) \end{array}\right) \\
& \quad = \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 \big( D_{\hat{T}_1} h\oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h \oplus 0_{\mathcal{E}_2}\big)\\ +
(I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \oplus 0_{E_n\otimes (\mathcal{D}_{\hat{T}_n}\oplus \mathcal{E}_1)} \\
i_1^* \big( D_{\hat{T}_1} h\oplus (I_n \otimes D_{\hat{T}_n} )(\tilde{T_n})^*h \oplus 0_{\mathcal{E}_1}\big) \end{array}\right) \\
& \quad = \left(\begin{array}{cc} 0_{E_{1n}\otimes \mathcal{D}_{\hat{T}_1}}\oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h \oplus 0_{E_n\otimes\mathcal{E}_1}\\ +
(I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \oplus 0_{E_n\otimes \mathcal{D}_{\hat{T}_n}}\oplus 0_{E_n\otimes\mathcal{E}_1}\\
D_{\hat{T}_1} h \end{array}\right) \\
& \quad = \left(\begin{array}{cc} (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h \oplus
(I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \oplus 0_{E_n\otimes\mathcal{E}_1}\\
D_{\hat{T}_1} h \end{array}\right) \\
& \quad = \left( \begin{array}{cc}
(I_n \otimes VD_{{\hat T}_{1n}}) (\tilde{T_n})^* h \\
D_{\hat{T}_1} h
\end{array} \right).
\end{align*}
\begin{align*}
& U_n\big(VD_{\hat{T}_{1n}}h, (I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h\big) \\
& \quad = U_n\big(D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1}, (I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \big) \\
& \quad = \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^* & i_1' \\ i_1^*U^* & 0 \end{array}\right) \left(\begin{array}{cc} D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1} \\ (I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \end{array}\right) \\
& \quad = \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^*\big( D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h \oplus 0_{\mathcal{E}_1}\big)\\
+
i_1' \big( (I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \big) \\
i_1^*U^*\big( D_{\hat{T}_n} h\oplus (I_1\otimes D_{\hat{T}_1} )(\tilde{T}_1)^*h\oplus 0_{\mathcal{E}_1} \big) \end{array}\right) \\
& \quad = \left(\begin{array}{cc} \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 \big( D_{\hat{T}_1} h\oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h \oplus 0_{\mathcal{E}_2}\big)\\ +
(I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \oplus 0_{E_n\otimes (\mathcal{D}_{\hat{T}_n}\oplus \mathcal{E}_1)} \\
i_1^* \big( D_{\hat{T}_1} h\oplus (I_n \otimes D_{\hat{T}_n} )(\tilde{T_n})^*h \oplus 0_{\mathcal{E}_1}\big) \end{array}\right) \\
& \quad = \left(\begin{array}{cc} 0_{E_{1n}\otimes \mathcal{D}_{\hat{T}_1}}\oplus (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h \oplus 0_{E_n\otimes\mathcal{E}_1}\\ +
(I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \oplus 0_{E_n\otimes \mathcal{D}_{\hat{T}_n}}\oplus 0_{E_n\otimes\mathcal{E}_1}\\
D_{\hat{T}_1} h \end{array}\right) \\
& \quad = \left(\begin{array}{cc} (I_n\otimes D_{\hat{T}_n} )(\tilde{T_n})^*h \oplus
(I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h \oplus 0_{E_n\otimes\mathcal{E}_1}\\
D_{\hat{T}_1} h \end{array}\right) \\
& \quad = \left( \begin{array}{cc}
(I_n \otimes VD_{{\hat T}_{1n}}) (\tilde{T_n})^* h \\
D_{\hat{T}_1} h
\end{array} \right).
\end{align*} That is, we can write  $U_n=\begin{bmatrix}A' & B'\\
C' & 0\end{bmatrix}$, where
$U_n=\begin{bmatrix}A' & B'\\
C' & 0\end{bmatrix}$, where  $A'=\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^*$,
$A'=\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2\big)P_2 U^*$, ![]() $B'=i_1'$, and
$B'=i_1'$, and ![]() $C'=i_1^*U^*$, which has the following property similar to that of U 1:
$C'=i_1^*U^*$, which has the following property similar to that of U 1:
 \begin{equation}
A'VD_{\hat{T}_{1n}}h+ B'[(I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h] = (I_n \otimes VD_{{\tilde T}_{1n}}) (\tilde{T_n})^* h
\end{equation}
\begin{equation}
A'VD_{\hat{T}_{1n}}h+ B'[(I_{1n}\otimes D_{\hat{T}_1} )(I_n\otimes (\tilde{T}_1)^*)(\tilde{T_n})^*h] = (I_n \otimes VD_{{\tilde T}_{1n}}) (\tilde{T_n})^* h
\end{equation}and
 \begin{equation}
C'VD_{\hat{T}_{1n}}h=D_{\hat{T}_1} h.
\end{equation}
\begin{equation}
C'VD_{\hat{T}_{1n}}h=D_{\hat{T}_1} h.
\end{equation}Recall that
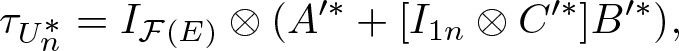 \begin{equation}
\tau_{U_n^*}=I_{\mathcal{F}(E)} \otimes (A'^*+[I_{1n}\otimes C'^*]B'^*),\end{equation}
\begin{equation}
\tau_{U_n^*}=I_{\mathcal{F}(E)} \otimes (A'^*+[I_{1n}\otimes C'^*]B'^*),\end{equation} where  $A'^*=UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)$,
$A'^*=UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)$, ![]() $B'^*=(i_1')^*$, and
$B'^*=(i_1')^*$, and ![]() $C'^*=Ui_1$, so that we can write
$C'^*=Ui_1$, so that we can write
 \begin{equation*}\tau_{U_n^*}=I_{\mathcal{F}(E)} \otimes \Big(UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)+[I_{1n}\otimes Ui_1](i_1')^*\Big).\end{equation*}
\begin{equation*}\tau_{U_n^*}=I_{\mathcal{F}(E)} \otimes \Big(UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)+[I_{1n}\otimes Ui_1](i_1')^*\Big).\end{equation*} The map ![]() $I_{1n}\otimes Ui_1$ is defined on
$I_{1n}\otimes Ui_1$ is defined on  $E_{1n}\otimes\mathcal{D}_{\hat{T}_1} $. Since this is the range of
$E_{1n}\otimes\mathcal{D}_{\hat{T}_1} $. Since this is the range of ![]() $(i_1')^*$,
$(i_1')^*$, ![]() $\tau_{U_n^*}$ is well defined. In fact,
$\tau_{U_n^*}$ is well defined. In fact,
where we view ![]() $\mathcal{F}(E)\otimes E_{1n}\otimes \mathcal{D}$ as a subspace of
$\mathcal{F}(E)\otimes E_{1n}\otimes \mathcal{D}$ as a subspace of ![]() $\mathcal{F}(E)\otimes \mathcal{D}$.
$\mathcal{F}(E)\otimes \mathcal{D}$.
So, as in proposition 3.13 and theorem 3.14, we have the following result,
Theorem 3.16 ![]() $\tau_{U_n^*}$ is an isometry and
$\tau_{U_n^*}$ is an isometry and  $(I_n\otimes\Pi_{1n,V})(\tilde{T_n})^*=\tau_{U_n^*}^*\Pi_{1n,V}$.
$(I_n\otimes\Pi_{1n,V})(\tilde{T_n})^*=\tau_{U_n^*}^*\Pi_{1n,V}$.
Proof. The fact that ![]() $\tau_{U_n^*}$ is an isometry follows from the proof of proposition 3.13. For
$\tau_{U_n^*}$ is an isometry follows from the proof of proposition 3.13. For ![]() $h\in H$,
$h\in H$, ![]() $\eta^{(\beta)}\in E^{\beta}$ and
$\eta^{(\beta)}\in E^{\beta}$ and  $k \in E_n\otimes \big(D_{\hat{T}_n}\oplus (E_1\otimes D_{\hat{T}_1}\oplus\mathcal{E}_1) \big)$, as in the proof of proposition 3.14,
$k \in E_n\otimes \big(D_{\hat{T}_n}\oplus (E_1\otimes D_{\hat{T}_1}\oplus\mathcal{E}_1) \big)$, as in the proof of proposition 3.14,
 \begin{align*}
&\langle \tau_{U_n^*}^*\Pi_{1n,V}h,\eta^{(\beta)}\otimes k\rangle\\
&\quad =\bigg\langle(I_{E^{\beta}} \otimes A'VD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h + [I_{E^{\beta}} \otimes B'(I_{1n} \otimes C'VD_{\hat{T}_{1n}}) \big(\tilde{T}_{1n}\big)^*]\\
& \qquad \times \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \bigg\rangle.
\end{align*}
\begin{align*}
&\langle \tau_{U_n^*}^*\Pi_{1n,V}h,\eta^{(\beta)}\otimes k\rangle\\
&\quad =\bigg\langle(I_{E^{\beta}} \otimes A'VD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h + [I_{E^{\beta}} \otimes B'(I_{1n} \otimes C'VD_{\hat{T}_{1n}}) \big(\tilde{T}_{1n}\big)^*]\\
& \qquad \times \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \bigg\rangle.
\end{align*}Using the properties of Un, listed in (3.26) and (3.27), this again equals to
 \begin{align*}
&\left\langle\big [I_{E^{\beta}} \otimes (I_n \otimes VD_{\hat{T}_{1n}}) (\tilde{T}_n)^* \big]\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \right\rangle \\
&\quad = \left\langle\Big [I_n\otimes (I_{E^{\beta}} \otimes VD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}\Big] (\tilde{T}_n)^*h,\eta^{(\beta)} \otimes k \right\rangle\\
&\quad =\left\langle(I_n\otimes\Pi_{1n,V})(\tilde{T_n})^*h,\eta^{(\beta)} \otimes k\right\rangle.
\end{align*}
\begin{align*}
&\left\langle\big [I_{E^{\beta}} \otimes (I_n \otimes VD_{\hat{T}_{1n}}) (\tilde{T}_n)^* \big]\left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}h, \eta^{(\beta)}\otimes k \right\rangle \\
&\quad = \left\langle\Big [I_n\otimes (I_{E^{\beta}} \otimes VD_{\hat{T}_{1n}}) \left(\tilde{\hat{T}}_{1n}\right)^{*(\beta)}\Big] (\tilde{T}_n)^*h,\eta^{(\beta)} \otimes k \right\rangle\\
&\quad =\left\langle(I_n\otimes\Pi_{1n,V})(\tilde{T_n})^*h,\eta^{(\beta)} \otimes k\right\rangle.
\end{align*} We now turn to show that ![]() $\tau_{U_i^*}$ gives rise to a representation of Ei on
$\tau_{U_i^*}$ gives rise to a representation of Ei on ![]() $K:=\mathcal{F}(E)\otimes \mathcal{D}$, where
$K:=\mathcal{F}(E)\otimes \mathcal{D}$, where ![]() $\mathcal{F}(E)$ is as in (3.18). It will be convenient to note that
$\mathcal{F}(E)$ is as in (3.18). It will be convenient to note that
 \begin{equation}
K=\mathcal{D}\oplus E_{1n}\otimes K \oplus\Big(\bigoplus_{i=2}^{n-1}E_i \otimes K\Big).
\end{equation}
\begin{equation}
K=\mathcal{D}\oplus E_{1n}\otimes K \oplus\Big(\bigoplus_{i=2}^{n-1}E_i \otimes K\Big).
\end{equation} In fact, there is a natural representation ρ on ![]() $\mathcal{B}(K)$,
$\mathcal{B}(K)$,
 \begin{equation*}\rho: M\to\mathcal{B}(K)=\mathcal{B}\Big(\mathcal{D} \oplus E_{1n}\otimes K \oplus\Big(\bigoplus_{i=2}^{n-1}E_{i}\otimes K\Big)\Big),\end{equation*}
\begin{equation*}\rho: M\to\mathcal{B}(K)=\mathcal{B}\Big(\mathcal{D} \oplus E_{1n}\otimes K \oplus\Big(\bigoplus_{i=2}^{n-1}E_{i}\otimes K\Big)\Big),\end{equation*}which is defined by
 \begin{align*}
\rho(a)=\varphi_{\mathcal{F}(E)}(a)\otimes I_{\mathcal{D}}=\rho_{\mathcal{D}}\oplus (\varphi_{1n}(a)\otimes I_{K})\oplus \Big(\bigoplus_{i=2}^{n-1}\varphi_i(a)\otimes I_{K}\Big),
\end{align*}
\begin{align*}
\rho(a)=\varphi_{\mathcal{F}(E)}(a)\otimes I_{\mathcal{D}}=\rho_{\mathcal{D}}\oplus (\varphi_{1n}(a)\otimes I_{K})\oplus \Big(\bigoplus_{i=2}^{n-1}\varphi_i(a)\otimes I_{K}\Big),
\end{align*} and we shall show that there are representations ![]() $(\rho,M_i)$ of Ei (
$(\rho,M_i)$ of Ei (![]() $i=1,n$) such that
$i=1,n$) such that  $\tau_{U_1^*}=\tilde{M}_1$ and
$\tau_{U_1^*}=\tilde{M}_1$ and  $\tau_{U_n^*}=\tilde{M}_n$ (in the notation of (2.3)).
$\tau_{U_n^*}=\tilde{M}_n$ (in the notation of (2.3)).
Proposition 3.17. Let K be as above. There are representations M 1 (of E 1) and Mn (of En) on ![]() $\mathcal{F}(E)\otimes\mathcal{D}$ such that
$\mathcal{F}(E)\otimes\mathcal{D}$ such that  $\tau_{U_1^*}=\tilde{M_1}$ and
$\tau_{U_1^*}=\tilde{M_1}$ and  $\tau_{U_n^*}=\tilde{M_n}$. Also, M 1 and Mn commute with Li for all
$\tau_{U_n^*}=\tilde{M_n}$. Also, M 1 and Mn commute with Li for all ![]() $i=2,\ldots,n-1$.
$i=2,\ldots,n-1$.
Proof. Let ![]() $a\in M$. First, we shall verify
$a\in M$. First, we shall verify
 \begin{equation}
\tilde{L}_1\big(\varphi_{1n}(a)\otimes I_{K}\big) =\rho(a)\tilde{L}_1\quad\,\,\, \tilde{L}_i\big(\varphi_{i}(a)\otimes I_{K}\big) =\rho(a)\tilde{L}_i\quad(\forall\,\,i=2,\ldots,n-1)
\end{equation}
\begin{equation}
\tilde{L}_1\big(\varphi_{1n}(a)\otimes I_{K}\big) =\rho(a)\tilde{L}_1\quad\,\,\, \tilde{L}_i\big(\varphi_{i}(a)\otimes I_{K}\big) =\rho(a)\tilde{L}_i\quad(\forall\,\,i=2,\ldots,n-1)
\end{equation}Then, we shall show
 \begin{equation}
\tau_{U_1^*}\big(\varphi_1(a)\otimes I_{K}\big) =\rho(a)\tau_{U_1^*}
\end{equation}
\begin{equation}
\tau_{U_1^*}\big(\varphi_1(a)\otimes I_{K}\big) =\rho(a)\tau_{U_1^*}
\end{equation}and
 \begin{equation}
\tau_{U_n^*}\big(\varphi_n(a)\otimes I_{K}\big) =\rho(a)\tau_{U_n^*}.
\end{equation}
\begin{equation}
\tau_{U_n^*}\big(\varphi_n(a)\otimes I_{K}\big) =\rho(a)\tau_{U_n^*}.
\end{equation} Once we verify these, the proposition will follow. To verify (3.31), we write, for ![]() $\xi\in E_{1n}$,
$\xi\in E_{1n}$, ![]() $\xi_i\in E_i$ and
$\xi_i\in E_i$ and ![]() $k\in K$,
$k\in K$,
and
Hence (3.31) follows. To prove (3.32), we will use (i) and (ii) that were proved in the proof of lemma 3.8. In fact, we shall use the adjoints, namely,
(i*)
 $P_1^*(I_1\otimes U^*)(\varphi_1(a)\otimes I_{\mathcal{D}})=\rho_{\mathcal{D}}(a)P_1^*(I_1\otimes U^*)$ and
$P_1^*(I_1\otimes U^*)(\varphi_1(a)\otimes I_{\mathcal{D}})=\rho_{\mathcal{D}}(a)P_1^*(I_1\otimes U^*)$ and(ii*)
 $(j'_2)^*(I_1\otimes U^*)(\varphi_1(a)\otimes I_{\mathcal{D}})=(\varphi_{1n}(a)\otimes I_{\mathcal{D}'})(j_2')^*(I_1\otimes U^*)$.
$(j'_2)^*(I_1\otimes U^*)(\varphi_1(a)\otimes I_{\mathcal{D}})=(\varphi_{1n}(a)\otimes I_{\mathcal{D}'})(j_2')^*(I_1\otimes U^*)$.
We now turn to prove (3.32). Note that the right-hand side is defined on ![]() $\mathcal{F}(E)\otimes E_1 \otimes \mathcal{D}$, but this is equal to
$\mathcal{F}(E)\otimes E_1 \otimes \mathcal{D}$, but this is equal to ![]() $E_1\otimes \mathcal{F}(E)\otimes \mathcal{D}$, so the left-hand side is also well defined. In fact, we can write
$E_1\otimes \mathcal{F}(E)\otimes \mathcal{D}$, so the left-hand side is also well defined. In fact, we can write
 \begin{equation*}E_1\otimes \mathcal{F}(E)\otimes \mathcal{D}=E_1\otimes \mathcal{D} \oplus \Big(\bigoplus_{\alpha\in\mathbb{Z}_+^{n-1},\,\alpha \gt 0}\big(E_1\otimes E^{\alpha}\otimes \mathcal{D}\big)\Big)\end{equation*}
\begin{equation*}E_1\otimes \mathcal{F}(E)\otimes \mathcal{D}=E_1\otimes \mathcal{D} \oplus \Big(\bigoplus_{\alpha\in\mathbb{Z}_+^{n-1},\,\alpha \gt 0}\big(E_1\otimes E^{\alpha}\otimes \mathcal{D}\big)\Big)\end{equation*} and proceed to prove the equality on ![]() $E_1\otimes \mathcal{D}$ and on
$E_1\otimes \mathcal{D}$ and on ![]() $E_1\otimes E^{\alpha}\otimes \mathcal{D}$. We start with
$E_1\otimes E^{\alpha}\otimes \mathcal{D}$. We start with ![]() $E_1\otimes \mathcal{D}$ and fix
$E_1\otimes \mathcal{D}$ and fix ![]() $\xi\otimes d\in E_1\otimes \mathcal{D}$.
$\xi\otimes d\in E_1\otimes \mathcal{D}$.
 \begin{align*}\tau_{U_1^*}(\varphi_1(a)\otimes I_{\mathcal{F}(E)\otimes \mathcal{D}})(\xi\otimes d)&=\tau_{U_1^*}(\varphi_1(a)\xi \otimes d)=(P_1^*(I_1\otimes U^*)\nonumber\\
& \quad + (I_{1n}\otimes i_2)(j_2')^*(I_1\otimes U^*))(\varphi_1(a)\xi \otimes d).\end{align*}
\begin{align*}\tau_{U_1^*}(\varphi_1(a)\otimes I_{\mathcal{F}(E)\otimes \mathcal{D}})(\xi\otimes d)&=\tau_{U_1^*}(\varphi_1(a)\xi \otimes d)=(P_1^*(I_1\otimes U^*)\nonumber\\
& \quad + (I_{1n}\otimes i_2)(j_2')^*(I_1\otimes U^*))(\varphi_1(a)\xi \otimes d).\end{align*}Using (i*) and (ii*), this is equal to
 \begin{align*}
\big(\rho_{\mathcal{D}}(a)&P_1^*(I_1\otimes U^*)+ (I_{1n}\otimes i_2)(\varphi_{1n}(a)\otimes I_{\mathcal{D}'})(j_2')^*(I_1\otimes U^*)\big)(\xi\otimes d)\\
=&\big(\rho_{\mathcal{D}}(a)P_1^*(I_1\otimes U^*)+(\varphi_{1n}(a)\otimes I_{\mathcal{D}})
(j_2')^*(I_1\otimes U^*)\big)(\xi\otimes d)\\
=&\big((\rho_{\mathcal{D}}(a)\oplus(\varphi_{1n}(a)\otimes I_{\mathcal{D}})\big)\big(P_1^*(I_1\otimes U^*) + (I_{1n}\otimes i_2)(j_2')^*(I_1\otimes U^*)\big)(\xi \otimes d)\\
=&\rho(a)\tau_{U_1^*}(\xi \otimes d),
\end{align*}
\begin{align*}
\big(\rho_{\mathcal{D}}(a)&P_1^*(I_1\otimes U^*)+ (I_{1n}\otimes i_2)(\varphi_{1n}(a)\otimes I_{\mathcal{D}'})(j_2')^*(I_1\otimes U^*)\big)(\xi\otimes d)\\
=&\big(\rho_{\mathcal{D}}(a)P_1^*(I_1\otimes U^*)+(\varphi_{1n}(a)\otimes I_{\mathcal{D}})
(j_2')^*(I_1\otimes U^*)\big)(\xi\otimes d)\\
=&\big((\rho_{\mathcal{D}}(a)\oplus(\varphi_{1n}(a)\otimes I_{\mathcal{D}})\big)\big(P_1^*(I_1\otimes U^*) + (I_{1n}\otimes i_2)(j_2')^*(I_1\otimes U^*)\big)(\xi \otimes d)\\
=&\rho(a)\tau_{U_1^*}(\xi \otimes d),
\end{align*} proving the statement (3.32) applied to ![]() $E_1\otimes \mathcal{D}$. Now, we apply the left-hand side of (3.32) to
$E_1\otimes \mathcal{D}$. Now, we apply the left-hand side of (3.32) to ![]() $\xi' \otimes d\in E_1\otimes E^{\alpha} \otimes \mathcal{D}$ (for
$\xi' \otimes d\in E_1\otimes E^{\alpha} \otimes \mathcal{D}$ (for  $\alpha\in\mathbb{Z}_+^{n-1},\alpha \gt 0$). But
$\alpha\in\mathbb{Z}_+^{n-1},\alpha \gt 0$). But ![]() $\xi'$ can also be written as
$\xi'$ can also be written as ![]() $\xi'\in E^{\alpha}\otimes E_1$, so we apply it to
$\xi'\in E^{\alpha}\otimes E_1$, so we apply it to ![]() $\xi'=\eta \otimes \xi$, where
$\xi'=\eta \otimes \xi$, where ![]() $\eta\in E^{\alpha} $ and
$\eta\in E^{\alpha} $ and ![]() $\xi\in E_1$, to get
$\xi\in E_1$, to get
 \begin{equation*}\tau_{U_1^*}\big(\varphi_1(a)\otimes I_{E^{\alpha} \otimes \mathcal{D}}\big)(\xi'\otimes d)=\tau_{U_1^*}\big(\varphi_1(a)\otimes I_{E^{\alpha} \otimes \mathcal{D}}\big)(\eta \otimes \xi\otimes d)\end{equation*}
\begin{equation*}\tau_{U_1^*}\big(\varphi_1(a)\otimes I_{E^{\alpha} \otimes \mathcal{D}}\big)(\xi'\otimes d)=\tau_{U_1^*}\big(\varphi_1(a)\otimes I_{E^{\alpha} \otimes \mathcal{D}}\big)(\eta \otimes \xi\otimes d)\end{equation*} \begin{equation*}=\tau_{U_1^*}\big(\varphi_{E^{\alpha}}(a)\eta \otimes \xi \otimes d\big)=\varphi_{E^{\alpha}}(a)\eta \otimes \tau_{U_1^*}(\xi \otimes d)\end{equation*}
\begin{equation*}=\tau_{U_1^*}\big(\varphi_{E^{\alpha}}(a)\eta \otimes \xi \otimes d\big)=\varphi_{E^{\alpha}}(a)\eta \otimes \tau_{U_1^*}(\xi \otimes d)\end{equation*} \begin{equation*}=\rho(a)(\eta \otimes \tau_{U_1^*}(\xi \otimes d))=\rho(a)\tau_{U_1^*}(\eta \otimes \xi \otimes d)=\rho(a)\tau_{U_1^*}(\xi' \otimes d).\end{equation*}
\begin{equation*}=\rho(a)(\eta \otimes \tau_{U_1^*}(\xi \otimes d))=\rho(a)\tau_{U_1^*}(\eta \otimes \xi \otimes d)=\rho(a)\tau_{U_1^*}(\xi' \otimes d).\end{equation*}This proves (3.32).
To prove (3.33), we will use (i) and (ii) that were proved in the proof of lemma 3.15. In fact, we shall use the adjoints, namely,
(i*)
 $ \rho_{\mathcal{D}}(a)UP_2^*(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2^*)=UP_2^*(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2^*)(\varphi_2(a)\otimes I_{\mathcal{D}})$ and
$ \rho_{\mathcal{D}}(a)UP_2^*(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2^*)=UP_2^*(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2^*)(\varphi_2(a)\otimes I_{\mathcal{D}})$ and(ii*)
 $(i_1')^*(\varphi_2(a)\otimes I_{\mathcal{D}})=(\varphi_{1n}(a) \otimes I_{\mathcal{D}_{\hat{T}_1}})(i_1')^*.$
$(i_1')^*(\varphi_2(a)\otimes I_{\mathcal{D}})=(\varphi_{1n}(a) \otimes I_{\mathcal{D}_{\hat{T}_1}})(i_1')^*.$
As in the proof of (3.32), we shall first prove it for ![]() $\xi \otimes d\in E_n\otimes \mathcal{D}$.
$\xi \otimes d\in E_n\otimes \mathcal{D}$.
So, we compute
 \begin{equation*}\tau_{U_n^*}(\varphi_2(a)\xi \otimes d)=UP_2^*(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2^*)(\varphi_2(a)\xi \otimes d) \oplus (I_{1n}\otimes Ui_1)(i_1')^*(\varphi_2(a)\xi\otimes d).\end{equation*}
\begin{equation*}\tau_{U_n^*}(\varphi_2(a)\xi \otimes d)=UP_2^*(I_{E_n\otimes \mathcal{D}_{1n}}\oplus u_2^*)(\varphi_2(a)\xi \otimes d) \oplus (I_{1n}\otimes Ui_1)(i_1')^*(\varphi_2(a)\xi\otimes d).\end{equation*}For the first summand, we use (i*) to find that it is equal to
For the second summand, we use (ii*) to write it as
and this is equal to
Putting it together, we get (3.33) for ![]() $E_2\otimes \mathcal{D})$.
$E_2\otimes \mathcal{D})$.
Now, we apply the left-hand side of (3.32) to ![]() $\xi' \otimes d\in E_n\otimes E^{\alpha} \otimes \mathcal{D}$ (for
$\xi' \otimes d\in E_n\otimes E^{\alpha} \otimes \mathcal{D}$ (for  $\alpha\in\mathbb{Z}_+^{n-1},\alpha \gt 0$). But
$\alpha\in\mathbb{Z}_+^{n-1},\alpha \gt 0$). But ![]() $E_n\otimes E^{\alpha}= E^{\alpha}\otimes E_n$, so it suffices to apply it to
$E_n\otimes E^{\alpha}= E^{\alpha}\otimes E_n$, so it suffices to apply it to ![]() $\xi'=\eta \otimes \xi$, where
$\xi'=\eta \otimes \xi$, where ![]() $\eta\in E^{\alpha} $ (α > 0) and
$\eta\in E^{\alpha} $ (α > 0) and ![]() $\xi\in E_n$, to get
$\xi\in E_n$, to get
 \begin{equation*}\tau_{U_n^*}(\varphi_2(a)\otimes I_{E_2\otimes E^{\alpha} \otimes \mathcal{D}})(\xi'\otimes d)=\tau_{U_n^*}(\varphi_{E^{\alpha}}(a)\eta \otimes \xi \otimes d)=\rho(a)\tau_{U_n^*}(\xi'\otimes d),\end{equation*}
\begin{equation*}\tau_{U_n^*}(\varphi_2(a)\otimes I_{E_2\otimes E^{\alpha} \otimes \mathcal{D}})(\xi'\otimes d)=\tau_{U_n^*}(\varphi_{E^{\alpha}}(a)\eta \otimes \xi \otimes d)=\rho(a)\tau_{U_n^*}(\xi'\otimes d),\end{equation*}proving (3.33).
For the remaining part of the proposition, we only prove that M 1 commutes with Li for all ![]() $i=2,\ldots,n-1$ as commutativity with Mn can be shown in a similar way. For all
$i=2,\ldots,n-1$ as commutativity with Mn can be shown in a similar way. For all ![]() $\xi_1\in E_1$,
$\xi_1\in E_1$, ![]() $\xi_i\in E_i$ and
$\xi_i\in E_i$ and ![]() $f=\eta\otimes d\in \mathcal{F}(E)\otimes\mathcal{D}$, we verify the following:
$f=\eta\otimes d\in \mathcal{F}(E)\otimes\mathcal{D}$, we verify the following:
 \begin{align*}
\tilde{M}_1(I_1\otimes \tilde{L}_i)(\xi_1\otimes\xi_i\otimes\eta\otimes d)=&\tau_{U_1^*}(\xi_1\otimes\xi_i\otimes\eta\otimes d)\\
=& \big[I_{\mathcal{F}(E)}\otimes\big(A^*+[I_{1n}\otimes C^*]B^*\big)\big](\xi_i\otimes\eta \otimes \xi_1\otimes d)\\
=& \xi_i\otimes\eta\otimes \big(A^*+[I_{1n}\otimes C^*]B^*\big)(\xi_1\otimes d)\\
=& \xi_i\otimes \big[I_{\mathcal{F}(E)}\otimes\big(A^*+[I_{1n}\otimes C^*]B^*\big)\big](\eta\otimes\xi_1\otimes d)\\
=& \xi_i\otimes\tau_{U_1^*}(\eta\otimes\xi_1\otimes d)\\
=& \tilde{L}_i\big( \xi_i\otimes\tau_{U_1^*}(\xi_1\otimes\eta\otimes d)\big)\\
=&\tilde{L}_i(I_i\otimes \tau_{U_1^*})(\xi_i\otimes\xi_1\otimes\eta\otimes d)\\
=& \tilde{L}_i(I_i\otimes \tilde{M}_1)(\xi_1\otimes\xi_i\otimes\eta\otimes d).
\end{align*}
\begin{align*}
\tilde{M}_1(I_1\otimes \tilde{L}_i)(\xi_1\otimes\xi_i\otimes\eta\otimes d)=&\tau_{U_1^*}(\xi_1\otimes\xi_i\otimes\eta\otimes d)\\
=& \big[I_{\mathcal{F}(E)}\otimes\big(A^*+[I_{1n}\otimes C^*]B^*\big)\big](\xi_i\otimes\eta \otimes \xi_1\otimes d)\\
=& \xi_i\otimes\eta\otimes \big(A^*+[I_{1n}\otimes C^*]B^*\big)(\xi_1\otimes d)\\
=& \xi_i\otimes \big[I_{\mathcal{F}(E)}\otimes\big(A^*+[I_{1n}\otimes C^*]B^*\big)\big](\eta\otimes\xi_1\otimes d)\\
=& \xi_i\otimes\tau_{U_1^*}(\eta\otimes\xi_1\otimes d)\\
=& \tilde{L}_i\big( \xi_i\otimes\tau_{U_1^*}(\xi_1\otimes\eta\otimes d)\big)\\
=&\tilde{L}_i(I_i\otimes \tau_{U_1^*})(\xi_i\otimes\xi_1\otimes\eta\otimes d)\\
=& \tilde{L}_i(I_i\otimes \tilde{M}_1)(\xi_1\otimes\xi_i\otimes\eta\otimes d).
\end{align*} This proves the commutativity of M 1 with Li, for all ![]() $i=2,\ldots,n-1$.
$i=2,\ldots,n-1$.
Now we consider the map  $\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})$, which is a product of the maps
$\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})$, which is a product of the maps ![]() $\tau_{U_n^*}:\mathcal{F}(E)\otimes E_n \otimes \mathcal{D} \rightarrow \mathcal{F}(E)\otimes \mathcal{D}$ and
$\tau_{U_n^*}:\mathcal{F}(E)\otimes E_n \otimes \mathcal{D} \rightarrow \mathcal{F}(E)\otimes \mathcal{D}$ and ![]() $I_1\otimes \tau_{U_n^*}:\mathcal{F}(E)\otimes E_1 \otimes E_n \otimes \mathcal{D} \rightarrow \mathcal{F}(E)\otimes E_1 \otimes \mathcal{D}$, respectively. Therefore, their product is well-defined, and it is
$I_1\otimes \tau_{U_n^*}:\mathcal{F}(E)\otimes E_1 \otimes E_n \otimes \mathcal{D} \rightarrow \mathcal{F}(E)\otimes E_1 \otimes \mathcal{D}$, respectively. Therefore, their product is well-defined, and it is
 \begin{equation*}\tau_{U_1^*}(I_1\otimes\tau_{U_n^*}):\mathcal{F}(E) \otimes E_{1n}\otimes \mathcal{D} \rightarrow \mathcal{F}(E)\otimes \mathcal{D}, \end{equation*}
\begin{equation*}\tau_{U_1^*}(I_1\otimes\tau_{U_n^*}):\mathcal{F}(E) \otimes E_{1n}\otimes \mathcal{D} \rightarrow \mathcal{F}(E)\otimes \mathcal{D}, \end{equation*} where ![]() $\mathcal{F}(E)\otimes E_{1n}\otimes \mathcal{D}$ can be viewed as a subspace of
$\mathcal{F}(E)\otimes E_{1n}\otimes \mathcal{D}$ can be viewed as a subspace of ![]() $\mathcal{F}(E)\otimes \mathcal{D}$.
$\mathcal{F}(E)\otimes \mathcal{D}$.
For the following theorem, we recall the definition of ![]() $\tilde{L}_1$ from (3.19) with the replacement of the coefficient space H by
$\tilde{L}_1$ from (3.19) with the replacement of the coefficient space H by ![]() $\mathcal{D}$ and so the map
$\mathcal{D}$ and so the map ![]() $\tilde{L}_1:E_{1n}\otimes\mathcal{F}(E)\otimes \mathcal{D} \to \mathcal{F}(E)\otimes \mathcal{D}$ is defined by
$\tilde{L}_1:E_{1n}\otimes\mathcal{F}(E)\otimes \mathcal{D} \to \mathcal{F}(E)\otimes \mathcal{D}$ is defined by
It is clear from the definition itself that ![]() $\tilde{L}_1$ is the inclusion of
$\tilde{L}_1$ is the inclusion of ![]() $E_{1n}\otimes\mathcal{F}(E)\otimes \mathcal{D}$ into
$E_{1n}\otimes\mathcal{F}(E)\otimes \mathcal{D}$ into ![]() $ \mathcal{F}(E)\otimes \mathcal{D}$. Now, we are ready to state the factorization results for the left-creation operator
$ \mathcal{F}(E)\otimes \mathcal{D}$. Now, we are ready to state the factorization results for the left-creation operator ![]() $\tilde{L}_1$.
$\tilde{L}_1$.
 \begin{equation*}\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})=\tilde{L}_1. \end{equation*}
\begin{equation*}\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})=\tilde{L}_1. \end{equation*}Proof. To calculate the map  $\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})$, we recall that
$\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})$, we recall that
 \begin{equation*}
P_1:\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} ) \oplus \mathcal{E}_1\rightarrow E_{1n}\otimes \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus E_1\otimes\mathcal{E}_2
\end{equation*}
\begin{equation*}
P_1:\mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} ) \oplus \mathcal{E}_1\rightarrow E_{1n}\otimes \mathcal{D}_{\hat{T}_n} \oplus (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus E_1\otimes\mathcal{E}_2
\end{equation*} is the projection onto the space  $E_1\otimes \mathcal{D}_{\hat{T}_1} $ and
$E_1\otimes \mathcal{D}_{\hat{T}_1} $ and
 \begin{equation*}
P_2: (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_2\rightarrow (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_2
\end{equation*}
\begin{equation*}
P_2: (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_2\rightarrow (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_2
\end{equation*} is the projection onto the space ![]() $(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2$. Now, observe that
$(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2$. Now, observe that
 \begin{align*}
I_1\otimes i_1^{'*}=I_{1n} \otimes \bar{i}_1^{'*},
\end{align*}
\begin{align*}
I_1\otimes i_1^{'*}=I_{1n} \otimes \bar{i}_1^{'*},
\end{align*} where  $\bar{i}_1^{'}: (E_1 \otimes \mathcal{D}_{\hat{T}_1}) \to (E_1 \otimes \mathcal{D}_{\hat{T}_1}) \oplus \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 $ is an inclusion. Using this, we have
$\bar{i}_1^{'}: (E_1 \otimes \mathcal{D}_{\hat{T}_1}) \to (E_1 \otimes \mathcal{D}_{\hat{T}_1}) \oplus \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 $ is an inclusion. Using this, we have
 \begin{align*}
& \Big[I_{\mathcal{F}(E)} \otimes P_1^*(I_1 \otimes U^*) \Big]
\Big[I_{\mathcal{F}(E)} \otimes I_1\otimes \big(I_{1n}\otimes Ui_1 \big)i_1^{'*} \Big] \\
& \quad = \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes P_1^*(I_1 \otimes U^*) \Big] \Big[\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes \big( I_1\otimes Ui_1 \big) \bar{i}_1^{'*} \Big]\\
& \quad = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes P_1^*(I_1 \otimes U^*) \big( I_1\otimes Ui_1 \big)\bar{i}_1^{'*} \\
& \quad = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes I_{1n} \otimes P_1^* \big( I_1\otimes i_1 \big) \bar{i}_1^{'*} \\
& \quad = I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes P_1^* \big( I_1\otimes i_1 \big) \Big) \Big( I_{1n} \otimes \bar{i}_1^{'*} \Big)
\\
& \quad = I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes P_1^* \big( I_1\otimes i_1 \big) \Big) \Big( I_1 \otimes i_1^{'*} \Big).
\end{align*}
\begin{align*}
& \Big[I_{\mathcal{F}(E)} \otimes P_1^*(I_1 \otimes U^*) \Big]
\Big[I_{\mathcal{F}(E)} \otimes I_1\otimes \big(I_{1n}\otimes Ui_1 \big)i_1^{'*} \Big] \\
& \quad = \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes P_1^*(I_1 \otimes U^*) \Big] \Big[\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes \big( I_1\otimes Ui_1 \big) \bar{i}_1^{'*} \Big]\\
& \quad = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes P_1^*(I_1 \otimes U^*) \big( I_1\otimes Ui_1 \big)\bar{i}_1^{'*} \\
& \quad = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes I_{1n} \otimes P_1^* \big( I_1\otimes i_1 \big) \bar{i}_1^{'*} \\
& \quad = I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes P_1^* \big( I_1\otimes i_1 \big) \Big) \Big( I_{1n} \otimes \bar{i}_1^{'*} \Big)
\\
& \quad = I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes P_1^* \big( I_1\otimes i_1 \big) \Big) \Big( I_1 \otimes i_1^{'*} \Big).
\end{align*}Similarly, since U is unitary, we also have
 \begin{align*}
&\Big[ I_{\mathcal{F}(E)} \otimes (I_{1n} \otimes i_2) j_2^{'*} (I_1 \otimes U^*) \Big] \Big[I_{\mathcal{F}(E)} \otimes I_1\otimes \big(I_{1n}\otimes Ui_1 \big)i_1^{'*} \Big] \\
& \quad = \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes (I_{1n} \otimes i_2) j_2^{'*} (I_1 \otimes U^*) \Big]
\Big[\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes \big( I_1\otimes Ui_1 \big)\bar{i}_1^{'*} \Big]\\
& \quad = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes (I_{1n} \otimes i_2) j_2^{'*} (I_1 \otimes U^*)
\big( I_1\otimes Ui_1 \big)\bar{i}_1^{'*} \\
& \quad = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes (I_{1n} \otimes i_2) j_2^{'*} ( I_1\otimes i_1 ) \bar{i}_1^{'*} \\
& \quad = I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes (I_{1n} \otimes i_2) j_2^{'*} ( I_1\otimes i_1 \big) \Big) \Big( I_{1n} \otimes \bar{i}_1^{'*} \Big) \\
& \quad = I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes (I_{1n} \otimes i_2) j_2^{'*} ( I_1\otimes i_1 \big) \Big) \Big( I_1 \otimes i_1^{'*} \Big).
\end{align*}
\begin{align*}
&\Big[ I_{\mathcal{F}(E)} \otimes (I_{1n} \otimes i_2) j_2^{'*} (I_1 \otimes U^*) \Big] \Big[I_{\mathcal{F}(E)} \otimes I_1\otimes \big(I_{1n}\otimes Ui_1 \big)i_1^{'*} \Big] \\
& \quad = \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes (I_{1n} \otimes i_2) j_2^{'*} (I_1 \otimes U^*) \Big]
\Big[\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes \big( I_1\otimes Ui_1 \big)\bar{i}_1^{'*} \Big]\\
& \quad = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes (I_{1n} \otimes i_2) j_2^{'*} (I_1 \otimes U^*)
\big( I_1\otimes Ui_1 \big)\bar{i}_1^{'*} \\
& \quad = \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes (I_{1n} \otimes i_2) j_2^{'*} ( I_1\otimes i_1 ) \bar{i}_1^{'*} \\
& \quad = I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes (I_{1n} \otimes i_2) j_2^{'*} ( I_1\otimes i_1 \big) \Big) \Big( I_{1n} \otimes \bar{i}_1^{'*} \Big) \\
& \quad = I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes (I_{1n} \otimes i_2) j_2^{'*} ( I_1\otimes i_1 \big) \Big) \Big( I_1 \otimes i_1^{'*} \Big).
\end{align*}By using the above identities, we compute the product of transfer functions corresponding to the unitaries U 1 and Un.
 \begin{align*}
&\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})\\
& \quad = \Big[I_{\mathcal{F}(E)}\otimes P_1^*(I_1\otimes U^*)\Big] \Big[I_{\mathcal{F}(E)}\otimes I_1\otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big]\\
& \qquad + \Big[I_{\mathcal{F}(E)} \otimes P_1^*(I_1 \otimes U^*) \Big]
\Big[I_{\mathcal{F}(E)} \otimes I_1\otimes \big(I_{1n}\otimes Ui_1 \big)i_1^{'*} \Big] \\
& \qquad + I_{\mathcal{F}(E)}\otimes \Big[ (I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes U^*)\Big(I_1\otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) \Big] \\
& \qquad + \Big[ I_{\mathcal{F}(E)} \otimes (I_{1n} \otimes i_2) j_2^{'*} (I_1 \otimes U^*) \Big] \Big[I_{\mathcal{F}(E)} \otimes I_1\otimes \big(I_{1n}\otimes Ui_1 \big)i_1^{'*} \Big] \\
& \quad = I_{\mathcal{F}(E)}\otimes P_1^*\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) + I_{\mathcal{F}(E)} \otimes\\
& \qquad \times \Big( I_{1n} \otimes P_1^* \big( I_1\otimes i_1 \big) \Big) \Big( I_1 \otimes i_1^{'*} \Big) \\
& \qquad + I_{\mathcal{F}(E)}\otimes (I_{1n}\otimes i_2)j_2^{'*}\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) \\
& \qquad + I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes (I_{1n} \otimes i_2) j_2^{'*} ( I_1\otimes i_1 \big) \Big) \Big( I_1 \otimes i_1^{'*} \Big) \\
& \quad =I_{\mathcal{F}(E)}\otimes\Big[P_1^*\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) + \big(I_{1n}\otimes P_1^*(I_1\otimes i_1)\big)(I_1\otimes i_1^{'*})\\
& \qquad +
(I_{1n}\otimes i_2)j_2^{'*} \Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big)\\
& \qquad +
\big(I_{1n}\otimes(I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes i_1)\big)(I_1\otimes i_1^{'*}) \Big].
\end{align*}
\begin{align*}
&\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})\\
& \quad = \Big[I_{\mathcal{F}(E)}\otimes P_1^*(I_1\otimes U^*)\Big] \Big[I_{\mathcal{F}(E)}\otimes I_1\otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big]\\
& \qquad + \Big[I_{\mathcal{F}(E)} \otimes P_1^*(I_1 \otimes U^*) \Big]
\Big[I_{\mathcal{F}(E)} \otimes I_1\otimes \big(I_{1n}\otimes Ui_1 \big)i_1^{'*} \Big] \\
& \qquad + I_{\mathcal{F}(E)}\otimes \Big[ (I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes U^*)\Big(I_1\otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) \Big] \\
& \qquad + \Big[ I_{\mathcal{F}(E)} \otimes (I_{1n} \otimes i_2) j_2^{'*} (I_1 \otimes U^*) \Big] \Big[I_{\mathcal{F}(E)} \otimes I_1\otimes \big(I_{1n}\otimes Ui_1 \big)i_1^{'*} \Big] \\
& \quad = I_{\mathcal{F}(E)}\otimes P_1^*\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) + I_{\mathcal{F}(E)} \otimes\\
& \qquad \times \Big( I_{1n} \otimes P_1^* \big( I_1\otimes i_1 \big) \Big) \Big( I_1 \otimes i_1^{'*} \Big) \\
& \qquad + I_{\mathcal{F}(E)}\otimes (I_{1n}\otimes i_2)j_2^{'*}\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) \\
& \qquad + I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes (I_{1n} \otimes i_2) j_2^{'*} ( I_1\otimes i_1 \big) \Big) \Big( I_1 \otimes i_1^{'*} \Big) \\
& \quad =I_{\mathcal{F}(E)}\otimes\Big[P_1^*\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) + \big(I_{1n}\otimes P_1^*(I_1\otimes i_1)\big)(I_1\otimes i_1^{'*})\\
& \qquad +
(I_{1n}\otimes i_2)j_2^{'*} \Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big)\\
& \qquad +
\big(I_{1n}\otimes(I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes i_1)\big)(I_1\otimes i_1^{'*}) \Big].
\end{align*}For the first term, note that
 \begin{align*}
\text{range}\Big(I_1 \otimes \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) = (E_{1n} \otimes \mathcal{D}_{\hat{T}_n}) \oplus (E_1\otimes E_{1n} \otimes \mathcal{D}_{\hat{T}_1})\oplus (E_1\otimes \mathcal{E}_2)
\end{align*}
\begin{align*}
\text{range}\Big(I_1 \otimes \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) = (E_{1n} \otimes \mathcal{D}_{\hat{T}_n}) \oplus (E_1\otimes E_{1n} \otimes \mathcal{D}_{\hat{T}_1})\oplus (E_1\otimes \mathcal{E}_2)
\end{align*}and
 \begin{align*}
& (I_1 \otimes P_2^*)\big((E_{1n} \otimes \mathcal{D}_{\hat{T}_n}) \oplus (E_1\otimes E_{1n} \otimes \mathcal{D}_{\hat{T}_1})\oplus (E_1\otimes \mathcal{E}_2)\big)\\
& \quad = (E_{1n} \otimes \mathcal{D}_{\hat{T}_n}) \oplus (E_1\otimes \mathcal{E}_2)\\
& \quad \subseteq (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_1\otimes \mathcal{E}_2)
\end{align*}
\begin{align*}
& (I_1 \otimes P_2^*)\big((E_{1n} \otimes \mathcal{D}_{\hat{T}_n}) \oplus (E_1\otimes E_{1n} \otimes \mathcal{D}_{\hat{T}_1})\oplus (E_1\otimes \mathcal{E}_2)\big)\\
& \quad = (E_{1n} \otimes \mathcal{D}_{\hat{T}_n}) \oplus (E_1\otimes \mathcal{E}_2)\\
& \quad \subseteq (E_1\otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} ) \oplus (E_1\otimes \mathcal{E}_2)
\end{align*} and P 1 is a projection on  $E_1 \otimes \mathcal{D}_{\hat{T}_1} $. So
$E_1 \otimes \mathcal{D}_{\hat{T}_1} $. So ![]() $(E_{1n} \otimes \mathcal{D}_{\hat{T}_n})\oplus (E_1\otimes \mathcal{E}_2) \subseteq \text{ker}P_1^*$ and hence
$(E_{1n} \otimes \mathcal{D}_{\hat{T}_n})\oplus (E_1\otimes \mathcal{E}_2) \subseteq \text{ker}P_1^*$ and hence
 \begin{equation*}P_1^*\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) = 0.\end{equation*}
\begin{equation*}P_1^*\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) = 0.\end{equation*}For the second term, we already have observed that
 \begin{equation*}
\big(I_{1n}\otimes P_1^*(I_1\otimes i_1)\big)(I_1\otimes i_1^{'*}) = I_{1n}\otimes \Big(P_1^*(I_1\otimes i_1) \bar{i}_1^{'*} \Big) .
\end{equation*}
\begin{equation*}
\big(I_{1n}\otimes P_1^*(I_1\otimes i_1)\big)(I_1\otimes i_1^{'*}) = I_{1n}\otimes \Big(P_1^*(I_1\otimes i_1) \bar{i}_1^{'*} \Big) .
\end{equation*}Now,
 \begin{equation*}
(E_1 \otimes \mathcal{D}_{\hat{T}_1})\oplus \mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_1 \xrightarrow{\bar{i}_1^{'*}} \ (E_1 \otimes \mathcal{D}_{\hat{T}_1}) \xrightarrow{I_1 \otimes i_1} \big( E_1 \otimes \mathcal{D}_{\hat{T}_1} \big) \oplus \big( E_{1n} \otimes \mathcal{D}_{\hat{T}_n} \big) \oplus \big( E_1 \otimes \mathcal{E}_2 \big).
\end{equation*}
\begin{equation*}
(E_1 \otimes \mathcal{D}_{\hat{T}_1})\oplus \mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_1 \xrightarrow{\bar{i}_1^{'*}} \ (E_1 \otimes \mathcal{D}_{\hat{T}_1}) \xrightarrow{I_1 \otimes i_1} \big( E_1 \otimes \mathcal{D}_{\hat{T}_1} \big) \oplus \big( E_{1n} \otimes \mathcal{D}_{\hat{T}_n} \big) \oplus \big( E_1 \otimes \mathcal{E}_2 \big).
\end{equation*} This tells us that  $(I_1\otimes i_1) \bar{i}_1^{'*}$ is an inclusion map with the range
$(I_1\otimes i_1) \bar{i}_1^{'*}$ is an inclusion map with the range  $E_1 \otimes \mathcal{D}_{\hat{T}_1}$. Since P 1 is a projection with range
$E_1 \otimes \mathcal{D}_{\hat{T}_1}$. Since P 1 is a projection with range  $E_1\otimes \mathcal{D}_{\hat{T}_1} $, so
$E_1\otimes \mathcal{D}_{\hat{T}_1} $, so  $\Big(P_1^*(I_1\otimes i_1) \bar{i}_1^{'*} \Big)$ is a projection with range
$\Big(P_1^*(I_1\otimes i_1) \bar{i}_1^{'*} \Big)$ is a projection with range  $E_1 \otimes \mathcal{D}_{\hat{T}_1}$ and hence
$E_1 \otimes \mathcal{D}_{\hat{T}_1}$ and hence
 \begin{equation*}
I_{1n}\otimes \Big(P_1^*(I_1\otimes i_1)\bar{i}_1^{'*} \Big) = P_{E_{1n} \otimes E_1 \otimes \mathcal{D}_{\hat{T}_1}}.
\end{equation*}
\begin{equation*}
I_{1n}\otimes \Big(P_1^*(I_1\otimes i_1)\bar{i}_1^{'*} \Big) = P_{E_{1n} \otimes E_1 \otimes \mathcal{D}_{\hat{T}_1}}.
\end{equation*}Now, we will calculate the third term. Observe that
 \begin{align*}
& (I_{1n}\otimes i_2)j_2^{'*}\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big)\\
& \quad =(I_{1n}\otimes i_2)\Big(I_{E_{1n}\otimes\mathcal{D}_{\hat{T}_n} }\oplus (I_1\otimes u_2)\Big)i_2^{'*}(I_1\otimes P_2^*)\Big(I_{E_{1n}\otimes\mathcal{D}_{1n}}\oplus (I_1\otimes u_2^*)\Big).
\end{align*}
\begin{align*}
& (I_{1n}\otimes i_2)j_2^{'*}\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big)\\
& \quad =(I_{1n}\otimes i_2)\Big(I_{E_{1n}\otimes\mathcal{D}_{\hat{T}_n} }\oplus (I_1\otimes u_2)\Big)i_2^{'*}(I_1\otimes P_2^*)\Big(I_{E_{1n}\otimes\mathcal{D}_{1n}}\oplus (I_1\otimes u_2^*)\Big).
\end{align*} The range of ![]() $I_{E_{1n}\otimes\mathcal{D}_{1n}}\oplus (I_1\otimes u_2^*)$ is
$I_{E_{1n}\otimes\mathcal{D}_{1n}}\oplus (I_1\otimes u_2^*)$ is  $(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes E_{1n} \otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_1\otimes\mathcal{E}_2)$. Also,
$(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes E_{1n} \otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_1\otimes\mathcal{E}_2)$. Also,
 \begin{align*}
& (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes E_{1n} \otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_1\otimes\mathcal{E}_2)\xrightarrow{I_1\otimes P_2^*} (E_1 \otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_{1n} \otimes\mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes\mathcal{E}_2)\\
& \quad \xrightarrow{i_2^{'*}} (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes\mathcal{E}_2).
\end{align*}
\begin{align*}
& (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes E_{1n} \otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_1\otimes\mathcal{E}_2)\xrightarrow{I_1\otimes P_2^*} (E_1 \otimes \mathcal{D}_{\hat{T}_1} )\oplus (E_{1n} \otimes\mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes\mathcal{E}_2)\\
& \quad \xrightarrow{i_2^{'*}} (E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes\mathcal{E}_2).
\end{align*}From the above inclusion, it follows that
 \begin{equation*}
i_2^{'*}(I_1\otimes P_2^*)=P_{(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes\mathcal{E}_2)}.
\end{equation*}
\begin{equation*}
i_2^{'*}(I_1\otimes P_2^*)=P_{(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes\mathcal{E}_2)}.
\end{equation*} Hence, keeping in mind that ![]() $i_2: \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1\to \mathcal{D} $ is an inclusion map, we conclude
$i_2: \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1\to \mathcal{D} $ is an inclusion map, we conclude
 \begin{align*}
& (I_{1n}\otimes i_2)j_2^{'*}\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big)\\
& \quad =(I_{1n}\otimes i_2)\Big(I_{E_{1n}\otimes\mathcal{D}_{\hat{T}_n} }\oplus (I_1\otimes u_2)\Big)P_{(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes\mathcal{E}_2)}\Big(I_{E_{1n}\otimes\mathcal{D}_{1n}}\oplus (I_1\otimes u_2^*)\Big)\\
& \quad = P_{(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_{1n}\otimes \mathcal{E}_1)}.
\end{align*}
\begin{align*}
& (I_{1n}\otimes i_2)j_2^{'*}\Big(I_1\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big)\\
& \quad =(I_{1n}\otimes i_2)\Big(I_{E_{1n}\otimes\mathcal{D}_{\hat{T}_n} }\oplus (I_1\otimes u_2)\Big)P_{(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_1\otimes\mathcal{E}_2)}\Big(I_{E_{1n}\otimes\mathcal{D}_{1n}}\oplus (I_1\otimes u_2^*)\Big)\\
& \quad = P_{(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_{1n}\otimes \mathcal{E}_1)}.
\end{align*} For the last term, observe that  $\text{ran}(I_1\otimes i_1)=E_1\otimes \mathcal{D}_{\hat{T}_1} $ which lies in the kernel of
$\text{ran}(I_1\otimes i_1)=E_1\otimes \mathcal{D}_{\hat{T}_1} $ which lies in the kernel of ![]() $j_2^{'*}$. So,
$j_2^{'*}$. So,  $j_2^{'*}(I_1\otimes i_1)=0$ and hence
$j_2^{'*}(I_1\otimes i_1)=0$ and hence
 \begin{equation*}
\big(I_{1n}\otimes(I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes i_1)\big)(I_1\otimes i_1^{'*}).
\end{equation*}
\begin{equation*}
\big(I_{1n}\otimes(I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes i_1)\big)(I_1\otimes i_1^{'*}).
\end{equation*}Therefore,
 \begin{align*}
\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})=&I_{\mathcal{F}(E)}\otimes
\Big[0 + P_{E_{1n} \otimes E_1 \otimes \mathcal{D}_{\hat{T}_1}} + P_{(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_{1n}\otimes \mathcal{E}_1)}+0\Big] \\
=&I_{\mathcal{F}(E)}\otimes I_{E_{1n} \otimes \big((E_1\otimes \mathcal{D}_{\hat{T}_1})\oplus\mathcal{D}_{\hat{T}_n}\oplus \mathcal{E}_1\big)}\\=&\tilde{L}_1.
\end{align*}
\begin{align*}
\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})=&I_{\mathcal{F}(E)}\otimes
\Big[0 + P_{E_{1n} \otimes E_1 \otimes \mathcal{D}_{\hat{T}_1}} + P_{(E_{1n} \otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_{1n}\otimes \mathcal{E}_1)}+0\Big] \\
=&I_{\mathcal{F}(E)}\otimes I_{E_{1n} \otimes \big((E_1\otimes \mathcal{D}_{\hat{T}_1})\oplus\mathcal{D}_{\hat{T}_n}\oplus \mathcal{E}_1\big)}\\=&\tilde{L}_1.
\end{align*} Below, we state another kind of factorization result for the left creation operator ![]() $\tilde{L}_1$.
$\tilde{L}_1$.
 \begin{equation*}\tau_{U_n^*}(I_n\otimes\tau_{U_1^*})=\tilde{L}_1.\end{equation*}
\begin{equation*}\tau_{U_n^*}(I_n\otimes\tau_{U_1^*})=\tilde{L}_1.\end{equation*}Proof. Observe that
 \begin{align*}
I_n\otimes j_2^{'*} & = I_n \otimes \Big[ \Big(I_{E_{1n} \otimes \mathcal{D}_{\hat{T}_n} } \oplus (I_1 \otimes u_2) \Big) \circ i_2^{'*} \Big] \\
& = \Big( I_n \otimes \Big[ I_{E_{1n} \otimes \mathcal{D}_{\hat{T}_n} } \oplus (I_1 \otimes u_2) \Big] \Big) \Big(I_n \otimes i_2^{'*} \Big) \\
&= \Big[ (I_n \otimes I_{1n} \otimes I_{\mathcal{D}_{\hat{T}_n} } ) \oplus (I_{1n} \otimes u_2) \Big] \Big(I_{1n} \otimes \bar{i}_2^{'*} \Big) \\
&= I_{1n} \otimes \Big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \Big) \bar{i}_2^{'*},
\end{align*}
\begin{align*}
I_n\otimes j_2^{'*} & = I_n \otimes \Big[ \Big(I_{E_{1n} \otimes \mathcal{D}_{\hat{T}_n} } \oplus (I_1 \otimes u_2) \Big) \circ i_2^{'*} \Big] \\
& = \Big( I_n \otimes \Big[ I_{E_{1n} \otimes \mathcal{D}_{\hat{T}_n} } \oplus (I_1 \otimes u_2) \Big] \Big) \Big(I_n \otimes i_2^{'*} \Big) \\
&= \Big[ (I_n \otimes I_{1n} \otimes I_{\mathcal{D}_{\hat{T}_n} } ) \oplus (I_{1n} \otimes u_2) \Big] \Big(I_{1n} \otimes \bar{i}_2^{'*} \Big) \\
&= I_{1n} \otimes \Big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \Big) \bar{i}_2^{'*},
\end{align*} where  $\bar{i}_2^{'}: (E_n \otimes \mathcal{D}_{\hat{T}_n}) \oplus \mathcal{E}_2 \to (E_n \otimes \mathcal{D}_{\hat{T}_n}) \oplus \mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_2 $ is an inclusion. So
$\bar{i}_2^{'}: (E_n \otimes \mathcal{D}_{\hat{T}_n}) \oplus \mathcal{E}_2 \to (E_n \otimes \mathcal{D}_{\hat{T}_n}) \oplus \mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_2 $ is an inclusion. So
 \begin{align*}
I_n\otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \big(I_1 \otimes U^*)
&= \big(I_{1n} \otimes I_n \otimes i_2 \big) \big( I_n \otimes j_2^{'*} \big) \big(I_{1n} \otimes U^*) \\
&= \big(I_{1n} \otimes I_n \otimes i_2 \big) \big( I_{1n} \otimes \Big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \Big) \bar{i}_2^{'*} \big) \big(I_{1n} \otimes U^* \big) \\
&= I_{1n} \otimes \big(I_n \otimes i_2 \big) \big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*}U^*.
\end{align*}
\begin{align*}
I_n\otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \big(I_1 \otimes U^*)
&= \big(I_{1n} \otimes I_n \otimes i_2 \big) \big( I_n \otimes j_2^{'*} \big) \big(I_{1n} \otimes U^*) \\
&= \big(I_{1n} \otimes I_n \otimes i_2 \big) \big( I_{1n} \otimes \Big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \Big) \bar{i}_2^{'*} \big) \big(I_{1n} \otimes U^* \big) \\
&= I_{1n} \otimes \big(I_n \otimes i_2 \big) \big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*}U^*.
\end{align*}Using the above identities, we have
 \begin{align*}
& \Big[I_{\mathcal{F}(E)} \otimes UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big]
\Big[I_{\mathcal{F}(E)} \otimes I_n \otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*}(I_1 \otimes U^*) \Big] \\
& \quad = \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big] \\
& \qquad \times \Big[\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes \big( I_n \otimes i_2 \big) \big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*} U^* \Big].
\end{align*}
\begin{align*}
& \Big[I_{\mathcal{F}(E)} \otimes UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big]
\Big[I_{\mathcal{F}(E)} \otimes I_n \otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*}(I_1 \otimes U^*) \Big] \\
& \quad = \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big] \\
& \qquad \times \Big[\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes \big( I_n \otimes i_2 \big) \big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*} U^* \Big].
\end{align*}Following the calculations at the beginning of the proof of theorem 3.18, the above quantity is equal to
 \begin{align*}
&I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big)
\Big( I_{1n} \otimes \big( I_n\otimes i_2 \big) \big(I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*}U^* \Big)
\\
&\quad \!\!\!\!\!= I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big)
\Big( I_n\otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \big(I_1 \otimes U^*) \Big)\\
&\quad \!\!\!\!\!= I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes U \Big) \Big( I_{1n} \otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big) \Big( I_n\otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \Big) \Big(I_{1n} \otimes U^* \Big). \end{align*}
\begin{align*}
&I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big)
\Big( I_{1n} \otimes \big( I_n\otimes i_2 \big) \big(I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*}U^* \Big)
\\
&\quad \!\!\!\!\!= I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big)
\Big( I_n\otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \big(I_1 \otimes U^*) \Big)\\
&\quad \!\!\!\!\!= I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes U \Big) \Big( I_{1n} \otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big) \Big( I_n\otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \Big) \Big(I_{1n} \otimes U^* \Big). \end{align*}Similarly, we also have
 \begin{align*}
&\Big[ I_{\mathcal{F}(E)} \otimes (I_{1n} \otimes Ui_1) i_1^{'*} \Big] \Big[I_{\mathcal{F}(E)} \otimes I_n \otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} (I_1 \otimes U^*) \Big] \\
&\quad = \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U \big)
\Big[ I_{\mathcal{F}(E)} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big] \Big[I_{\mathcal{F}(E)} \otimes I_n \otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \Big]\\
&\qquad \times \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U^* \big) \\
&\quad = \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U \big) \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big] \\
&\qquad \times \Big[\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes \big( I_n \otimes i_2 \big)
\big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*} \Big]
\big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U^* \big) \\
&\quad = \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U \big)
\Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes (I_{1n} \otimes i_1) i_1^{'*} (I_n \otimes i_2)\\
& \qquad \times \big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*} \Big]
\big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U^* \big) \\
&\quad = \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U \big) \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes I_{1n} \otimes (I_{1n} \otimes i_1) i_1^{'*} (I_n \otimes i_2)\\
& \qquad \times
\big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*} \Big]\big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U^* \big) \\
&\quad \!= I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes I_{1n} \otimes U\Big)\Big( I_{1n} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big) \Big( I_n \otimes \big( I_{1n} \otimes i_2 \big) j_2^{'*} \Big) \big( I_{1n} \otimes U^* \big) .
\end{align*}
\begin{align*}
&\Big[ I_{\mathcal{F}(E)} \otimes (I_{1n} \otimes Ui_1) i_1^{'*} \Big] \Big[I_{\mathcal{F}(E)} \otimes I_n \otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} (I_1 \otimes U^*) \Big] \\
&\quad = \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U \big)
\Big[ I_{\mathcal{F}(E)} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big] \Big[I_{\mathcal{F}(E)} \otimes I_n \otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \Big]\\
&\qquad \times \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U^* \big) \\
&\quad = \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U \big) \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big] \\
&\qquad \times \Big[\bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes \big( I_n \otimes i_2 \big)
\big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*} \Big]
\big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U^* \big) \\
&\quad = \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U \big)
\Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{(\alpha+e_1)}} \otimes (I_{1n} \otimes i_1) i_1^{'*} (I_n \otimes i_2)\\
& \qquad \times \big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*} \Big]
\big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U^* \big) \\
&\quad = \big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U \big) \Big[ \bigoplus_{\alpha \in \mathbb{Z}_+^{n-1}} I_{E^{\alpha}} \otimes I_{1n} \otimes (I_{1n} \otimes i_1) i_1^{'*} (I_n \otimes i_2)\\
& \qquad \times
\big( I_{E_n \otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 \big) \bar{i}_2^{'*} \Big]\big( I_{\mathcal{F}(E)} \otimes I_{1n} \otimes U^* \big) \\
&\quad \!= I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes I_{1n} \otimes U\Big)\Big( I_{1n} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big) \Big( I_n \otimes \big( I_{1n} \otimes i_2 \big) j_2^{'*} \Big) \big( I_{1n} \otimes U^* \big) .
\end{align*}Combining all the above identities, we compute the following:
 \begin{align*}
&\tau_{U_n^*}(I_n\otimes\tau_{U_1^*})\\
& \quad =\Big(I_{\mathcal{F}(E)}\otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big)\Big(I_{\mathcal{F}(E)}\otimes I_n\otimes P_1^*(I_1\otimes U^*)\Big)\\
&\qquad+ \Big(I_{\mathcal{F}(E)} \otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) \Big(I_{\mathcal{F}(E)}\otimes I_n\otimes (I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes U^*)\Big)\\
&\qquad+ \Big(I_{\mathcal{F}(E)} \otimes [I_{1n}\otimes Ui_1]i_1^{'*}\Big) \Big(I_{\mathcal{F}(E)}\otimes I_n\otimes P_1^*(I_1\otimes U^*)\Big)\\
&\qquad+ \Big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes Ui_1]i_1^{'*}\Big)
\Big(I_{\mathcal{F}(E)}\otimes I_n\otimes (I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes U^*)\Big)\\
& \quad =I_{\mathcal{F}(E)}\otimes UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \big( I_n\otimes P_1^* \big) (I_{1n}\otimes U^*)\\
&\qquad+ I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes U \Big) \Big( I_{1n} \otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big) \Big( I_n\otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \Big) \Big(I_{1n} \otimes U^* \Big)\\
&\qquad+ I_{\mathcal{F}(E)}\otimes \big(I_{1n}\otimes U \big)
\big( I_{1n} \otimes i_1 \big) i_1^{'*} \big( I_n\otimes P_1^* \big) \big(I_{1n} \otimes U^* \big)\\
&\qquad+ I_{\mathcal{F}(E)} \otimes \big( I_{1n} \otimes I_{1n} \otimes U \big) \Big( I_{1n} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big) \Big( I_n \otimes \big( I_{1n} \otimes i_2 \big) j_2^{'*} \Big) \big(I_{1n} \otimes U^* \big).
\end{align*}
\begin{align*}
&\tau_{U_n^*}(I_n\otimes\tau_{U_1^*})\\
& \quad =\Big(I_{\mathcal{F}(E)}\otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big)\Big(I_{\mathcal{F}(E)}\otimes I_n\otimes P_1^*(I_1\otimes U^*)\Big)\\
&\qquad+ \Big(I_{\mathcal{F}(E)} \otimes UP_2^* \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)\Big) \Big(I_{\mathcal{F}(E)}\otimes I_n\otimes (I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes U^*)\Big)\\
&\qquad+ \Big(I_{\mathcal{F}(E)} \otimes [I_{1n}\otimes Ui_1]i_1^{'*}\Big) \Big(I_{\mathcal{F}(E)}\otimes I_n\otimes P_1^*(I_1\otimes U^*)\Big)\\
&\qquad+ \Big(I_{\mathcal{F}(E)}\otimes [I_{1n}\otimes Ui_1]i_1^{'*}\Big)
\Big(I_{\mathcal{F}(E)}\otimes I_n\otimes (I_{1n}\otimes i_2)j_2^{'*}(I_1\otimes U^*)\Big)\\
& \quad =I_{\mathcal{F}(E)}\otimes UP_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \big( I_n\otimes P_1^* \big) (I_{1n}\otimes U^*)\\
&\qquad+ I_{\mathcal{F}(E)} \otimes \Big( I_{1n} \otimes U \Big) \Big( I_{1n} \otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big) \Big) \Big( I_n\otimes \big(I_{1n}\otimes i_2 \big)j_2^{'*} \Big) \Big(I_{1n} \otimes U^* \Big)\\
&\qquad+ I_{\mathcal{F}(E)}\otimes \big(I_{1n}\otimes U \big)
\big( I_{1n} \otimes i_1 \big) i_1^{'*} \big( I_n\otimes P_1^* \big) \big(I_{1n} \otimes U^* \big)\\
&\qquad+ I_{\mathcal{F}(E)} \otimes \big( I_{1n} \otimes I_{1n} \otimes U \big) \Big( I_{1n} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big) \Big( I_n \otimes \big( I_{1n} \otimes i_2 \big) j_2^{'*} \Big) \big(I_{1n} \otimes U^* \big).
\end{align*}For the first term, note that
 \begin{equation*}
\text{range}(I_n \otimes P_1^*) = E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \subseteq (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_{1n} \otimes \mathcal{D}_{\hat{T}_1} ) \oplus (E_n\otimes \mathcal{E}_1),
\end{equation*}
\begin{equation*}
\text{range}(I_n \otimes P_1^*) = E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \subseteq (E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus (E_{1n} \otimes \mathcal{D}_{\hat{T}_1} ) \oplus (E_n\otimes \mathcal{E}_1),
\end{equation*} and it follows that  $\text{range}\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n \otimes P_1^*) = E_{1n} \otimes \mathcal{D}_{\hat{T}_1}$, which lies in the kernel of
$\text{range}\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n \otimes P_1^*) = E_{1n} \otimes \mathcal{D}_{\hat{T}_1}$, which lies in the kernel of ![]() $P_2^*$ and hence
$P_2^*$ and hence  $P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes P_1^*) = 0$.
$P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes P_1^*) = 0$.
For the second term, we already have observed that
 \begin{align*}
& \big(I_{1n}\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes i_2)\big)(I_n\otimes j_2^{'*})\\
& \quad = I_{1n}\otimes \Big(P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 ) \bar{i}_2^{'*} \Big).
\end{align*}
\begin{align*}
& \big(I_{1n}\otimes P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes i_2)\big)(I_n\otimes j_2^{'*})\\
& \quad = I_{1n}\otimes \Big(P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 ) \bar{i}_2^{'*} \Big).
\end{align*}Now,
 \begin{align*}
& \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 )\\
& \quad =\big(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_1} }\oplus I_{E_n\otimes \mathcal{D}_{\hat{T}_n} }\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 )\\
& \quad =\big(0_{E_{1n}\otimes \mathcal{D}_{\hat{T}_1} }\oplus I_{E_n\otimes \mathcal{D}_{\hat{T}_n} }\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 )\\
& \quad = i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2},
\end{align*}
\begin{align*}
& \big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 )\\
& \quad =\big(I_{E_{1n}\otimes \mathcal{D}_{\hat{T}_1} }\oplus I_{E_n\otimes \mathcal{D}_{\hat{T}_n} }\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 )\\
& \quad =\big(0_{E_{1n}\otimes \mathcal{D}_{\hat{T}_1} }\oplus I_{E_n\otimes \mathcal{D}_{\hat{T}_n} }\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 )\\
& \quad = i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2},
\end{align*} where  $i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2}:(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2\to \big( E_n \otimes \mathcal{D}_{\hat{T}_n} \big) \oplus \big( E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \big) \oplus \mathcal{E}_2$ is an inclusion and the last line follows since
$i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2}:(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2\to \big( E_n \otimes \mathcal{D}_{\hat{T}_n} \big) \oplus \big( E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \big) \oplus \mathcal{E}_2$ is an inclusion and the last line follows since ![]() $I_n \otimes i_2$ is an inclusion map with range
$I_n \otimes i_2$ is an inclusion map with range  $E_n \otimes \big( \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 \big)$. So,
$E_n \otimes \big( \mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1 \big)$. So,
 \begin{equation*}
P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 ) \bar{i}_2^{'*}=P_2^* (i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2}) \bar{i}_2^{'*}.
\end{equation*}
\begin{equation*}
P_2^*\big(I_{E_n\otimes\mathcal{D}_{1n}}\oplus u_2^*\big)(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 ) \bar{i}_2^{'*}=P_2^* (i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2}) \bar{i}_2^{'*}.
\end{equation*}Observe that
 \begin{align*}
& (E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus\mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_2\xrightarrow{\bar{i}_2^{'*}} (E_n \otimes \mathcal{D}_{\hat{T}_n}) \oplus \mathcal{E}_2\xrightarrow{i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2}}\\
& \quad \times \big( E_n \otimes \mathcal{D}_{\hat{T}_n} \big) \oplus \big( E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \big) \oplus \mathcal{E}_2\xrightarrow{P_2^*} (E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus \mathcal{E}_2.
\end{align*}
\begin{align*}
& (E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus\mathcal{D}_{\hat{T}_1} \oplus \mathcal{E}_2\xrightarrow{\bar{i}_2^{'*}} (E_n \otimes \mathcal{D}_{\hat{T}_n}) \oplus \mathcal{E}_2\xrightarrow{i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2}}\\
& \quad \times \big( E_n \otimes \mathcal{D}_{\hat{T}_n} \big) \oplus \big( E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \big) \oplus \mathcal{E}_2\xrightarrow{P_2^*} (E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus \mathcal{E}_2.
\end{align*}So,
 \begin{equation*}
P_2^* (i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2})\bar{i}_2^{'*} =P_{(E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus \mathcal{E}_2}.
\end{equation*}
\begin{equation*}
P_2^* (i_{(E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2})\bar{i}_2^{'*} =P_{(E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus \mathcal{E}_2}.
\end{equation*}Hence,
 \begin{equation*}
I_{1n}\otimes \Big(P_2^*(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 ) \bar{i}_2^{'*} \Big) = P_{E_{1n} \otimes \big((E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus \mathcal{E}_2\big)}.
\end{equation*}
\begin{equation*}
I_{1n}\otimes \Big(P_2^*(I_n\otimes i_2) (I_{E_n\otimes \mathcal{D}_{\hat{T}_n} } \oplus u_2 ) \bar{i}_2^{'*} \Big) = P_{E_{1n} \otimes \big((E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus \mathcal{E}_2\big)}.
\end{equation*}Now, for the third term, we consider the following diagram:
 \begin{align*}
& E_{1n}\otimes \mathcal{D}_{\hat{T}_1} \xrightarrow[]{I_n \otimes P_1^*} E_n \otimes \big(\mathcal{D}_{\hat{T}_n} \oplus ( E_{1} \otimes \mathcal{D}_{\hat{T}_1} ) \oplus \mathcal{E}_1 \big)\\
& \quad \xrightarrow[]{i_1^{'*}} \big( E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \big)
\xrightarrow[]{I_{1n}\otimes i_1}\ E_{1n} \otimes \big(\mathcal{D}_{\hat{T}_1} \oplus( E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2 \big)
\end{align*}
\begin{align*}
& E_{1n}\otimes \mathcal{D}_{\hat{T}_1} \xrightarrow[]{I_n \otimes P_1^*} E_n \otimes \big(\mathcal{D}_{\hat{T}_n} \oplus ( E_{1} \otimes \mathcal{D}_{\hat{T}_1} ) \oplus \mathcal{E}_1 \big)\\
& \quad \xrightarrow[]{i_1^{'*}} \big( E_{1n} \otimes \mathcal{D}_{\hat{T}_1} \big)
\xrightarrow[]{I_{1n}\otimes i_1}\ E_{1n} \otimes \big(\mathcal{D}_{\hat{T}_1} \oplus( E_n\otimes \mathcal{D}_{\hat{T}_n} )\oplus \mathcal{E}_2 \big)
\end{align*} with the help of range $(I_n \otimes P_1^*) = E_{1n} \otimes \mathcal{D}_{\hat{T}_1} $ it is easy to observe that
$(I_n \otimes P_1^*) = E_{1n} \otimes \mathcal{D}_{\hat{T}_1} $ it is easy to observe that
 \begin{equation*} (I_{1n}\otimes i_1)i_1^{'*}(I_n\otimes P_1^*) = P_{E_{1n} \otimes \mathcal{D}_{\hat{T}_1} }. \end{equation*}
\begin{equation*} (I_{1n}\otimes i_1)i_1^{'*}(I_n\otimes P_1^*) = P_{E_{1n} \otimes \mathcal{D}_{\hat{T}_1} }. \end{equation*} For the last term, first note that  $\text{ran}\, j_2^{'*} = E_{1n} \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)$, so
$\text{ran}\, j_2^{'*} = E_{1n} \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)$, so  $\text{ran}(I_{1n}\otimes i_2) j_2^{'*} = E_{1n} \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)$ and hence
$\text{ran}(I_{1n}\otimes i_2) j_2^{'*} = E_{1n} \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)$ and hence  $\text{ran}\big(I_n\otimes (I_{1n}\otimes i_2) j_2^{'*}\big) = E_{1n}\otimes E_n \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)$. On the other hand,
$\text{ran}\big(I_n\otimes (I_{1n}\otimes i_2) j_2^{'*}\big) = E_{1n}\otimes E_n \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)$. On the other hand,  $E_n \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)\subseteq \text{ker}\, i_1^{'*}$, which implies
$E_n \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)\subseteq \text{ker}\, i_1^{'*}$, which implies  $E_{1n}\otimes E_n \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)\subseteq \text{ker}(I_{1n}\otimes i_1^{'*})$. Therefore,
$E_{1n}\otimes E_n \otimes (\mathcal{D}_{\hat{T}_n} \oplus \mathcal{E}_1)\subseteq \text{ker}(I_{1n}\otimes i_1^{'*})$. Therefore,
 \begin{align*}
& \big( I_{1n} \otimes I_{1n} \otimes U \big) \Big( I_{1n} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big) \Big( I_n \otimes \big( I_{1n} \otimes i_2 \big) j_2^{'*} \Big) \big(I_{1n} \otimes U^* \big)\\
& \quad =\big(\! I_{1n} \otimes I_{1n} \otimes U \big)(I_{1n} \otimes I_{1n} \otimes i_1)(I_{1n}\otimes i_1^{'*}) \Big(\! I_n \otimes \big( I_{1n} \otimes i_2 \big) j_2^{'*} \Big) \big(I_{1n} \otimes U^* \big)=0.
\end{align*}
\begin{align*}
& \big( I_{1n} \otimes I_{1n} \otimes U \big) \Big( I_{1n} \otimes (I_{1n} \otimes i_1) i_1^{'*} \Big) \Big( I_n \otimes \big( I_{1n} \otimes i_2 \big) j_2^{'*} \Big) \big(I_{1n} \otimes U^* \big)\\
& \quad =\big(\! I_{1n} \otimes I_{1n} \otimes U \big)(I_{1n} \otimes I_{1n} \otimes i_1)(I_{1n}\otimes i_1^{'*}) \Big(\! I_n \otimes \big( I_{1n} \otimes i_2 \big) j_2^{'*} \Big) \big(I_{1n} \otimes U^* \big)=0.
\end{align*}Therefore,
 \begin{align*}
& \tau_{U_n^*}(I_n\otimes\tau_{U_1^*})\\
&\quad =I_{\mathcal{F}(E)} \otimes (I_{1n}\otimes U)
\Big[0 + P_{E_{1n} \otimes \big((E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus \mathcal{E}_2\big)} +
P_{E_{1n}\otimes \mathcal{D}_{\hat{T}_1}} + 0 \Big](I_{1n}\otimes U^*) \\
&\quad =I_{\mathcal{F}(E)}\otimes(I_{1n}\otimes U)
\Big[ I_{E_{1n} \otimes \big((E_n\otimes \mathcal{D}_{\hat{T}_n})\oplus\mathcal{D}_{\hat{T}_1}\oplus \mathcal{E}_2\big)} \Big](I_{1n}\otimes U^*) \\
&\quad =I_{\mathcal{F}(E)}\otimes I_{E_{1n} \otimes \big((E_1\otimes \mathcal{D}_{\hat{T}_1})\oplus\mathcal{D}_{\hat{T}_n}\oplus \mathcal{E}_1\big)}\\
&\quad =\tilde{L}_1.
\end{align*}
\begin{align*}
& \tau_{U_n^*}(I_n\otimes\tau_{U_1^*})\\
&\quad =I_{\mathcal{F}(E)} \otimes (I_{1n}\otimes U)
\Big[0 + P_{E_{1n} \otimes \big((E_n \otimes \mathcal{D}_{\hat{T}_n})\oplus \mathcal{E}_2\big)} +
P_{E_{1n}\otimes \mathcal{D}_{\hat{T}_1}} + 0 \Big](I_{1n}\otimes U^*) \\
&\quad =I_{\mathcal{F}(E)}\otimes(I_{1n}\otimes U)
\Big[ I_{E_{1n} \otimes \big((E_n\otimes \mathcal{D}_{\hat{T}_n})\oplus\mathcal{D}_{\hat{T}_1}\oplus \mathcal{E}_2\big)} \Big](I_{1n}\otimes U^*) \\
&\quad =I_{\mathcal{F}(E)}\otimes I_{E_{1n} \otimes \big((E_1\otimes \mathcal{D}_{\hat{T}_1})\oplus\mathcal{D}_{\hat{T}_n}\oplus \mathcal{E}_1\big)}\\
&\quad =\tilde{L}_1.
\end{align*}Combining the above results, we have the following dilation theorem:
Theorem 3.20 Let ![]() $(\sigma,T_1,\ldots,T_n)\in\mathcal{T}_{1,n}^n(\sigma,\,M,\,E_1,\ldots,E_n,H)$ and let E,
$(\sigma,T_1,\ldots,T_n)\in\mathcal{T}_{1,n}^n(\sigma,\,M,\,E_1,\ldots,E_n,H)$ and let E, ![]() $\mathcal{D}$,
$\mathcal{D}$, ![]() $\Pi_{1n,V}:H\to \mathcal{F}(E)\otimes \mathcal{D}$ and
$\Pi_{1n,V}:H\to \mathcal{F}(E)\otimes \mathcal{D}$ and ![]() $L_i\, (i=2,\ldots,n)$ as above. Then,
$L_i\, (i=2,\ldots,n)$ as above. Then, ![]() $\Pi_{1n,V}$ is an isometry and
$\Pi_{1n,V}$ is an isometry and
 \begin{equation*}\begin{cases}
(I_1\otimes\Pi_{1n,V})(\tilde{T}_1)^*=\tau_{U_1^*}^*\Pi_{1n,V}\\
(I_i\otimes\Pi_{1n,V})(\tilde{T}_i)^*=(\tilde{L}_i)^*\Pi_{1n,V}\quad \text{for}\,\,\,2\leq i\leq n-1\\
(I_n\otimes\Pi_{1n,V})(\tilde{T_n})^*=\tau_{U_n^*}^*\Pi_{1n,V},
\end{cases}
\end{equation*}
\begin{equation*}\begin{cases}
(I_1\otimes\Pi_{1n,V})(\tilde{T}_1)^*=\tau_{U_1^*}^*\Pi_{1n,V}\\
(I_i\otimes\Pi_{1n,V})(\tilde{T}_i)^*=(\tilde{L}_i)^*\Pi_{1n,V}\quad \text{for}\,\,\,2\leq i\leq n-1\\
(I_n\otimes\Pi_{1n,V})(\tilde{T_n})^*=\tau_{U_n^*}^*\Pi_{1n,V},
\end{cases}
\end{equation*} where ![]() $\tau_{U_1^*}$ and
$\tau_{U_1^*}$ and ![]() $\tau_{U_n^*}$ are the multiplication operators that are isometries and have transfer function-type representations with respect to some unitaries U 1 and Un, respectively. Moreover,
$\tau_{U_n^*}$ are the multiplication operators that are isometries and have transfer function-type representations with respect to some unitaries U 1 and Un, respectively. Moreover, ![]() $\tau_{U_1^*}$ and
$\tau_{U_1^*}$ and ![]() $\tau_{U_n^*}$ satisfy the following relation:
$\tau_{U_n^*}$ satisfy the following relation:
 \begin{equation*}
\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})=\tilde{L}_1=\tau_{U_n^*}(I_n\otimes\tau_{U_1^*}),
\end{equation*}
\begin{equation*}
\tau_{U_1^*}(I_1\otimes\tau_{U_n^*})=\tilde{L}_1=\tau_{U_n^*}(I_n\otimes\tau_{U_1^*}),
\end{equation*} and there is an isometric representation ![]() $(\rho, M_1, L_2,\ldots,L_{n-1},M_n)$ of the product system that dilates the representation
$(\rho, M_1, L_2,\ldots,L_{n-1},M_n)$ of the product system that dilates the representation ![]() $(\sigma,T_1,\ldots,T_n)$ and such that
$(\sigma,T_1,\ldots,T_n)$ and such that  $\tau_{U_i^*}=\tilde{M_i}$ for
$\tau_{U_i^*}=\tilde{M_i}$ for ![]() $i=1,n$.
$i=1,n$.
4. Applications
Theorem 4.1 Let M be a von Neumann algebra and ![]() $\alpha_1,\alpha_2,\ldots,\alpha_n$ be
$\alpha_1,\alpha_2,\ldots,\alpha_n$ be ![]() $*$-automorphisms of M that pairwise commute. Also, let σ be a normal representation of M on a Hilbert space H and let
$*$-automorphisms of M that pairwise commute. Also, let σ be a normal representation of M on a Hilbert space H and let ![]() $t:=(t_1,t_2,\ldots,t_n )$ be a commuting tuple of operators in B(H) such that
$t:=(t_1,t_2,\ldots,t_n )$ be a commuting tuple of operators in B(H) such that
(i) t satisfies the conditions from [Reference Barik, Das, Haria and Sarkar4] :
 $\hat{t}_1$ and
$\hat{t}_1$ and  $\hat{t}_n$ satisfy Szegö positivity and
$\hat{t}_n$ satisfy Szegö positivity and  $\hat{t}_n$ is pure.
$\hat{t}_n$ is pure.(ii) for every
 $a\in M$ and
$a\in M$ and  $1\leq i \leq n$,
(4.1)
$1\leq i \leq n$,
(4.1) \begin{equation}
t_i\sigma(\alpha_i(a))=\sigma(a)t_i.
\end{equation}
\begin{equation}
t_i\sigma(\alpha_i(a))=\sigma(a)t_i.
\end{equation}
Then, there is a Hilbert space K, an isometry ![]() $V:H\rightarrow K$, a representation ρ of M on K and commuting isometries
$V:H\rightarrow K$, a representation ρ of M on K and commuting isometries ![]() $v_1,\ldots.v_n$ in B(K) that satisfy
$v_1,\ldots.v_n$ in B(K) that satisfy
and dilate ![]() $(\sigma,t_1,\ldots,t_n)$, that is,
$(\sigma,t_1,\ldots,t_n)$, that is,
(i)
 $\sigma(a)=V^*\rho(a)V$ for all
$\sigma(a)=V^*\rho(a)V$ for all  $a\in M$ and
$a\in M$ and(ii)
 $Vt_i^*=v_i^*V$ for all i
$Vt_i^*=v_i^*V$ for all i
Setting ![]() $\alpha_i=id_M$ above, we get
$\alpha_i=id_M$ above, we get
Corollary 4.2. Let M be a von Neumann algebra, σ be a normal representation of M on a Hilbert space H, and ![]() $t:=(t_1,t_2,\ldots,t_n )$ be a commuting tuple of operators in B(H) such that
$t:=(t_1,t_2,\ldots,t_n )$ be a commuting tuple of operators in B(H) such that
(i) t satisfies the conditions from [Reference Barik, Das, Haria and Sarkar4] :
 $\hat{t}_1$ and
$\hat{t}_1$ and  $\hat{t}_n$ satisfy Szegö positivity and
$\hat{t}_n$ satisfy Szegö positivity and  $\hat{t}_n$ is pure.
$\hat{t}_n$ is pure.(ii) for every
 $1\leq i \leq n$,
$1\leq i \leq n$,  $t_i\in \sigma(M)'$.
$t_i\in \sigma(M)'$.
Then, there is a Hilbert space K , an isometry ![]() $V:H\rightarrow K$, a representation ρ of M on K, and commuting isometries
$V:H\rightarrow K$, a representation ρ of M on K, and commuting isometries ![]() $v_1,\ldots.v_n$ in
$v_1,\ldots.v_n$ in ![]() $\rho(M)'$ that dilate
$\rho(M)'$ that dilate ![]() $(\sigma,t_1,\ldots,t_n)$, that is,
$(\sigma,t_1,\ldots,t_n)$, that is,
(i)
 $\sigma(a)=V^*\rho(a)V$ for all
$\sigma(a)=V^*\rho(a)V$ for all  $a\in M$ and
$a\in M$ and(ii)
 $Vt_i^*=v_i^*V$ for all i.
$Vt_i^*=v_i^*V$ for all i.
To prove the theorem, we explain how theorem 4.1 is related to theorem 3.20.
For this, we first note that, given an ![]() $*$-automorphism α of a von Neumann algebra M, one can associate a
$*$-automorphism α of a von Neumann algebra M, one can associate a ![]() $W^*$-correspondence, written
$W^*$-correspondence, written ![]() $_{\alpha}M$, with it. As a vector space,
$_{\alpha}M$, with it. As a vector space, ![]() $_{\alpha}M$ is M. The M-valued inner product is
$_{\alpha}M$ is M. The M-valued inner product is ![]() $\langle a,b \rangle =a^*b$, the left multiplication is
$\langle a,b \rangle =a^*b$, the left multiplication is ![]() $m \cdot a=ma$, and the right multiplication is
$m \cdot a=ma$, and the right multiplication is ![]() $\varphi(m)a=\alpha(m)a$ (where m and a are in M but a here is viewed as an element of the correspondence).
$\varphi(m)a=\alpha(m)a$ (where m and a are in M but a here is viewed as an element of the correspondence).
If α and β are two automorphisms of M, then
where the isomorphism is given by ![]() $a\otimes b \mapsto \beta(a)b$. Thus, we will identify
$a\otimes b \mapsto \beta(a)b$. Thus, we will identify ![]() $_{\alpha}M\otimes _{\beta}M $ with
$_{\alpha}M\otimes _{\beta}M $ with ![]() $ _{\beta \alpha}M $, and when α and β commute, we identify
$ _{\beta \alpha}M $, and when α and β commute, we identify ![]() $_{\alpha}M\otimes _{\beta}M $ with
$_{\alpha}M\otimes _{\beta}M $ with ![]() $_{\beta}M\otimes _{\alpha}M $.
$_{\beta}M\otimes _{\alpha}M $.
Now, let ![]() $(T,\sigma)$ be a representation of
$(T,\sigma)$ be a representation of ![]() $_{\alpha}M$. We have, for
$_{\alpha}M$. We have, for ![]() $a,b\in M$,
$a,b\in M$, ![]() $T(\alpha(a)b)=T(\varphi(a)b)=\sigma(a)T(b)$. Setting b = I, we get
$T(\alpha(a)b)=T(\varphi(a)b)=\sigma(a)T(b)$. Setting b = I, we get ![]() $T(\alpha(a))=\sigma(a)T(I)$. But
$T(\alpha(a))=\sigma(a)T(I)$. But ![]() $T(\alpha(a))=T(I\cdot \alpha(a))=T(I)\sigma(\alpha(a))$, and writing
$T(\alpha(a))=T(I\cdot \alpha(a))=T(I)\sigma(\alpha(a))$, and writing ![]() $t:=T(I)$, we get
$t:=T(I)$, we get ![]() $t\sigma(\alpha(a))=\sigma(a)t$ for every
$t\sigma(\alpha(a))=\sigma(a)t$ for every ![]() $a\in M$. So, a representation of this correspondence is given by a normal representation σ on H and a contraction
$a\in M$. So, a representation of this correspondence is given by a normal representation σ on H and a contraction ![]() $t\in B(H)$ satisfying the intertwining relation
$t\in B(H)$ satisfying the intertwining relation
for all ![]() $a\in M$ (see [Reference Muhly and Solel10] for details). Note also that
$a\in M$ (see [Reference Muhly and Solel10] for details). Note also that ![]() $_{\alpha}M\otimes_{\sigma}H\cong H$ via the isomorphism
$_{\alpha}M\otimes_{\sigma}H\cong H$ via the isomorphism ![]() $a\otimes h\mapsto \sigma(a)h$. Identifying
$a\otimes h\mapsto \sigma(a)h$. Identifying ![]() $_{\alpha}M\otimes_{\sigma}H$ with H, we find that
$_{\alpha}M\otimes_{\sigma}H$ with H, we find that ![]() $\tilde{T}$ can be viewed as an operator in B(H). With these identifications, we write
$\tilde{T}$ can be viewed as an operator in B(H). With these identifications, we write
In fact, ![]() $t=\tilde{T}(I\otimes h)$ and
$t=\tilde{T}(I\otimes h)$ and ![]() $t\sigma(a)h=\tilde{T}(I\otimes_{\sigma}\sigma(a)h)=\tilde{T}(a\otimes h)$.
$t\sigma(a)h=\tilde{T}(I\otimes_{\sigma}\sigma(a)h)=\tilde{T}(a\otimes h)$.
Now, suppose that ![]() $(\sigma,T)$ is a representation of
$(\sigma,T)$ is a representation of ![]() $_{\alpha}M$ and
$_{\alpha}M$ and ![]() $(\sigma,S)$ is a representation of
$(\sigma,S)$ is a representation of ![]() $_{\beta}M$. Recall that, when we identify
$_{\beta}M$. Recall that, when we identify ![]() $_{\alpha}M\otimes _{\beta}M$ with
$_{\alpha}M\otimes _{\beta}M$ with ![]() $_{\beta \alpha}M$,
$_{\beta \alpha}M$,  $I_{_{\beta \alpha}M}$ is identified with
$I_{_{\beta \alpha}M}$ is identified with  $I_{_{\alpha}M}\otimes I_{_{\beta}M}$ and, thus,
$I_{_{\alpha}M}\otimes I_{_{\beta}M}$ and, thus,
 \begin{equation} \tilde{S}(I_{_{\beta}M}\otimes \tilde{T})(I_{_{\beta \alpha}M}\otimes h)=\tilde{S}(I_{_{\beta}M}\otimes \tilde{T})(I_{_{\alpha}M}\otimes I_{_{\beta}M}\otimes h)=\tilde{S}(I_{_\beta M}\otimes th)=sth.\end{equation}
\begin{equation} \tilde{S}(I_{_{\beta}M}\otimes \tilde{T})(I_{_{\beta \alpha}M}\otimes h)=\tilde{S}(I_{_{\beta}M}\otimes \tilde{T})(I_{_{\alpha}M}\otimes I_{_{\beta}M}\otimes h)=\tilde{S}(I_{_\beta M}\otimes th)=sth.\end{equation} Thus,  $\tilde{S}(I_{_{\beta}M}\otimes \tilde{T})$ is associated with st. A straightforward computation using the identifications above shows that
$\tilde{S}(I_{_{\beta}M}\otimes \tilde{T})$ is associated with st. A straightforward computation using the identifications above shows that ![]() $(\tilde{T})^*k=t^*k$ and
$(\tilde{T})^*k=t^*k$ and
For every representation ![]() $(\sigma,T)$,
$(\sigma,T)$,
and we conclude that ![]() $(\sigma,T)$ is isometric if and only if t is an isometry.
$(\sigma,T)$ is isometric if and only if t is an isometry.
We now turn to prove theorem 4.1.
Proof. We now fix the setting of theorem 4.1. That is, we fix a von Neumann algebra M and pairwise commuting automorphisms ![]() $\alpha_1,\alpha_2,\ldots,\alpha_n$ on M. Also, we fix a normal representation σ of M on a Hilbert space H, and let
$\alpha_1,\alpha_2,\ldots,\alpha_n$ on M. Also, we fix a normal representation σ of M on a Hilbert space H, and let ![]() $t:=(t_1,t_2,\ldots,t_n )$ be a commuting tuple of operators in B(H) such that
$t:=(t_1,t_2,\ldots,t_n )$ be a commuting tuple of operators in B(H) such that
(i) t satisfies the conditions from [Reference Barik, Das, Haria and Sarkar4] :
 $\hat{t}_1$ and
$\hat{t}_1$ and  $\hat{t}_n$ satisfy Szegö positivity and
$\hat{t}_n$ satisfy Szegö positivity and  $\hat{t}_n$ is pure.
$\hat{t}_n$ is pure.(ii) for every
 $a\in M$ and
$a\in M$ and  $1\leq i \leq n$,
(4.6)
$1\leq i \leq n$,
(4.6) \begin{equation}
t_i\sigma(\alpha_i(a))=\sigma(a)t_i.
\end{equation}
\begin{equation}
t_i\sigma(\alpha_i(a))=\sigma(a)t_i.
\end{equation}
Since ![]() $\{\alpha_i\}$ pairwise commute, we can identify
$\{\alpha_i\}$ pairwise commute, we can identify  $_{\alpha_i}M\otimes _{\alpha_j}M $ with
$_{\alpha_i}M\otimes _{\alpha_j}M $ with  $_{\alpha_j}M\otimes _{\alpha_i}M $ (as above), and
$_{\alpha_j}M\otimes _{\alpha_i}M $ (as above), and ![]() $(M,_{\alpha_1}M,\ldots,_{\alpha_n}M)$ defines a product system. Equation (4.6) implies that each ti gives rise to a representation
$(M,_{\alpha_1}M,\ldots,_{\alpha_n}M)$ defines a product system. Equation (4.6) implies that each ti gives rise to a representation ![]() $(\sigma, T_i)$ of
$(\sigma, T_i)$ of ![]() $_{\alpha_i}M$ and the associated
$_{\alpha_i}M$ and the associated ![]() $\tilde{T_i}$ satisfies
$\tilde{T_i}$ satisfies ![]() $t_i=\tilde{T_i}(I\otimes h)$ and
$t_i=\tilde{T_i}(I\otimes h)$ and ![]() $t_i\sigma(a)h=\tilde{T_i}(I\otimes_{\sigma}\sigma(a)h)=\tilde{T_i}(a\otimes h)$. Equation (4.4) shows that these representations pairwise commute and, thus, define a representation of the product system.
$t_i\sigma(a)h=\tilde{T_i}(I\otimes_{\sigma}\sigma(a)h)=\tilde{T_i}(a\otimes h)$. Equation (4.4) shows that these representations pairwise commute and, thus, define a representation of the product system.
Since the Szegö condition and the pureness conditions involve expressions of the form ![]() $t_it_j^*$ (for operators) or
$t_it_j^*$ (for operators) or  $\tilde{T}_i\tilde{T_j}^*$ (for representations), it follows from (4.5) that (i) in theorem 4.1 implies that
$\tilde{T}_i\tilde{T_j}^*$ (for representations), it follows from (4.5) that (i) in theorem 4.1 implies that ![]() $(\sigma,T_1,\ldots,T_n)\in\mathcal{T}_{1,n}^n(\sigma,\,M,\,E_1,\ldots,E_n,H)$ and, thus, theorem 3.20 applies.
$(\sigma,T_1,\ldots,T_n)\in\mathcal{T}_{1,n}^n(\sigma,\,M,\,E_1,\ldots,E_n,H)$ and, thus, theorem 3.20 applies.
We conclude that there is an isometric representation ![]() $(\rho, M_1, L_2,\ldots,L_{n-1},M_n)$ of the product system that dilates the representation
$(\rho, M_1, L_2,\ldots,L_{n-1},M_n)$ of the product system that dilates the representation ![]() $(\sigma,T_1,\ldots,T_n)$ and such that
$(\sigma,T_1,\ldots,T_n)$ and such that  $\tau_{U_i^*}=\tilde{M_i}$ for
$\tau_{U_i^*}=\tilde{M_i}$ for ![]() $i=1,2$.
$i=1,2$.
Writing the isometric representation ![]() $(\rho, M_1, L_2,\ldots,L_{n-1},M_n)$ as
$(\rho, M_1, L_2,\ldots,L_{n-1},M_n)$ as ![]() $(\rho, V_1, V_2,\ldots,V_{n-1},V_n)$ (and let
$(\rho, V_1, V_2,\ldots,V_{n-1},V_n)$ (and let ![]() $v_i=V_i(I)$ as above), this completes the proof of the theorem.
$v_i=V_i(I)$ as above), this completes the proof of the theorem.
(i) The isometries vi can be written explicitly as shown in theorem 3.20.
(ii) For
 $M=\mathbb{C}$ (and writing vi explicitly as noted in (i)), we get the main result of [Reference Barik, Das, Haria and Sarkar4].
$M=\mathbb{C}$ (and writing vi explicitly as noted in (i)), we get the main result of [Reference Barik, Das, Haria and Sarkar4].
Acknowledgements
We are grateful to the referees for their careful and rigorous reading of the article and for making several fruitful comments/suggestions to enhance the quality of the article. S.B. and M.B. are grateful to Prof. Bata Krishna Das for some insightful discussions at the beginning of this project. Part of S.B.’s research was carried out at the Ben-Gurion University, and the research is partially supported by the Israel Science Foundation grant number 2196-20. M.B.’s research is supported by the DST-INSPIRE Faculty Fellowship No. DST/INSPIRE/04/2020/001250.