Published online by Cambridge University Press: 25 September 2020
A directed space is a topological space 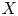 $X$ together with a subspace
$X$ together with a subspace 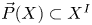 $\vec {P}(X)\subset X^I$ of directed paths on
$\vec {P}(X)\subset X^I$ of directed paths on 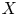 $X$. A symmetry of a directed space should therefore respect both the topology of the underlying space and the topology of the associated spaces
$X$. A symmetry of a directed space should therefore respect both the topology of the underlying space and the topology of the associated spaces 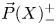 $\vec {P}(X)_-^+$ of directed paths between a source (
$\vec {P}(X)_-^+$ of directed paths between a source ( $-$) and a target (
$-$) and a target (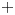 $+$)—up to homotopy. If it is, moreover, homotopic to the identity map—in a directed sense—such a symmetry will be called an inessential d-map, and the paper explores the algebra and topology of inessential d-maps. Comparing two d-spaces
$+$)—up to homotopy. If it is, moreover, homotopic to the identity map—in a directed sense—such a symmetry will be called an inessential d-map, and the paper explores the algebra and topology of inessential d-maps. Comparing two d-spaces  $X$ and
$X$ and 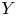 $Y$ ‘up to symmetry’ yields the notion of a directed homotopy equivalence between them. Under appropriate conditions, all directed homotopy equivalences are shown to satisfy a 2-out-of-3 property. Our notion of directed homotopy equivalence does not agree completely with the one defined in Goubault (2017, arxiv:1709:05702v2) and Goubault, Farber and Sagnier (2020, J. Appl. Comput. Topol. 4, 11–27); the deviation is motivated by examples. Nevertheless, directed topological complexity, introduced in Goubault, Farber and Sagnier (2020) is shown to be invariant under our notion of directed homotopy equivalence. Finally, we show that directed homotopy equivalences result in isomorphisms on the pair component categories of directed spaces introduced in Goubault, Farber and Sagnier (2020).
$Y$ ‘up to symmetry’ yields the notion of a directed homotopy equivalence between them. Under appropriate conditions, all directed homotopy equivalences are shown to satisfy a 2-out-of-3 property. Our notion of directed homotopy equivalence does not agree completely with the one defined in Goubault (2017, arxiv:1709:05702v2) and Goubault, Farber and Sagnier (2020, J. Appl. Comput. Topol. 4, 11–27); the deviation is motivated by examples. Nevertheless, directed topological complexity, introduced in Goubault, Farber and Sagnier (2020) is shown to be invariant under our notion of directed homotopy equivalence. Finally, we show that directed homotopy equivalences result in isomorphisms on the pair component categories of directed spaces introduced in Goubault, Farber and Sagnier (2020).