Hostname: page-component-745bb68f8f-lrblm Total loading time: 0 Render date: 2025-01-13T09:52:28.371Z Has data issue: false hasContentIssue false
  • English
  • Français

The idempotent generated subsemigroup of the semigroup of continuous endomorphisms of a separable Hilbert space

Published online by Cambridge University Press:  14 November 2011

R. J. H. Dawlings
R. J. H. Dawlings
Affiliation:
Bayero University, PMB 3011, Kano, Nigeria
Get access Rights & Permissions [Opens in a new window]

Extract

Let H be a separable Hilbert space and let CL(H) be the semigroup of continuous, linear maps from H to H. Let E+ be the idempotents of CL(H). Let Ker ɑ and Im ɑ be the null-space and range, respectively, of an element ɑ of CL(H) and let St ɑ be the subspace {x∊H: xɑ = x} of H. It is shown that 〈E+〉 = I∪F∪{i}, where

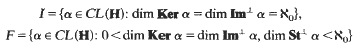
and ι is the identity map. From the proof it is clear that I and F both form subsemigroups of 〈E+〉 and that the depth of I is 3. It is also shown that the depths of F and 〈E+〉 are infinite.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 94 , Issue 3-4 , 1983 , pp. 351 - 360
Copyright
Copyright © Royal Society of Edinburgh 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Berberian, S. K.. Introduction to Hilbert Space (Oxford University Press, 1961).Google Scholar
2Dawlings, R. J. H.. Semigroups of Singular Endomorphisms of Vector Spaces (Ph.D. Thesis, Univ. of St Andrews, 1980).Google Scholar
3Dawlings, R. J. H.. Products of idempotents in the semigroup of singular endomorphisms of a finite-dimensional vector space. Proc. Roy. Soc. Edinburgh Sect. A 91 (1981), 123–133.CrossRefGoogle Scholar
4Erdos, J. A.. On products of idempotent matrices. Glasgow Math. J. 8 (1967), 118–122.CrossRefGoogle Scholar
5Howie, J. M.. The subsemigroup generated by the idempotents of a full transformation semigroup. J. London Math. Soc. 41 (1966), 707–716.CrossRefGoogle Scholar
6Howie, J. M.. Some subsemigroups of infinite full transformation semigroups. Proc. Roy. Soc. Edinburgh Sect. A 88 (1981), 159–167.CrossRefGoogle Scholar
7Simmons, G. F.. Introduction to Topology and Modern Analysis (New York: McGraw–Hill, 1963).Google Scholar