Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-16T15:50:23.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Holomorphically embedded discs with rapidly growing area

Published online by Cambridge University Press:  14 November 2011

Josip Globevnik
Josip Globevnik
Affiliation:
Department of Mathematics, University of Ljubljana, 19 Jadranska, 1000 Ljubljana, Slovenia
Get access Rights & Permissions [Opens in a new window]

Abstract

It is shown that if V is a closed submanifold of the open unit ball 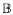of ℂ2 biholomorphically equivalent to a disc, then the area of V ∩ r 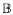can grow arbitrarily rapidly as r ↗ 1. It is also shown that if V is a closed submanifold of ℂ2 biholomorphically equivalent to a disc, then the area of V ∩ r 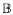can grow arbitrarily rapidly as r ↗ ∞.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 129 , Issue 2 , 1999 , pp. 343 - 349
Copyright
Copyright © Royal Society of Edinburgh 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Forstnerič, F., Globevnik, J. and Rosay, J.-P.. Non straightenable complex lines in ℂ2. Ark. Mat. 34 (1996), 97–101.CrossRefGoogle Scholar
2Forstnerič, F., Globevnik, J. and Stensones, B.. Embedding holomorphic discs through discrete sets. Math. Ann. 305 (1996), 559–569.CrossRefGoogle Scholar
3Globevnik, J. and Stensones, B.. Holomorphic embeddings of planar domains into ℂ2. Math. Ann. 303 (1995), 579–597.CrossRefGoogle Scholar
4Globevnik, J. and Stout, E. L.. The ends of varieties. Am. J. Math. 108 (1986), 1355–1410.CrossRefGoogle Scholar
5Narasimhan, R.. Imbeddings of holomorphically complete spaces. Am. J. Math. 82 (1960), 917–934.CrossRefGoogle Scholar