Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-19T11:26:59.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher order Wirtinger inequalities

Published online by Cambridge University Press:  14 November 2011

Kurt Kreith  and
Charles A. Swanson
Kurt Kreith
Affiliation:
University of California, Davis, Calif., U.S.A.
Charles A. Swanson
Affiliation:
University of British Columbia, Vancouver, Canada
Get access Rights & Permissions [Opens in a new window]

Synopsis

Wirtinger-type inequalities of order n are inequalities between quadratic forms involving derivatives of order k ≦ n of admissible functions in an interval (a, b). Several methods for establishing these inequalities are investigated, leading to improvements of classical results as well as systematic generation of new ones. A Wirtinger inequality for Hamiltonian systems is obtained in which standard regularity hypotheses are weakened and singular intervals are permitted, and this is employed to generalize standard inequalities for linear differential operators of even order. In particular second order inequalities of Beesack's type are developed, in which the admissible functions satisfy only the null boundary conditions at the endpoints of [a, b] and b does not exceed the first systems conjugate point 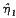(a) of a. Another approach is presented involving the standard minimization theory of quadratic forms and the theory of “natural boundary conditions”. Finally, inequalities of order n + k are described in terms of (n, n)-disconjugacy of associated 2nth order differential operators.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 85 , Issue 1-2 , 1980 , pp. 87 - 110
Copyright
Copyright © Royal Society of Edinburgh 1980

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Agmon, S.. Lectures on Elliptic Boundary Value Problems (Princeton, N.J.: Van Nostrana, 1965).Google Scholar
2Banks, D. O.. Bounds for eigenvalues and conditions for existence of conjugate points. SIAM J. Appl. Math. 27 (1974), 365–375.CrossRefGoogle Scholar
3Barrett, J.. Systems-disconjugacy of a fourth order differential equation. Proc. Amer. Math. Soc. 12 (1961), 205–213.Google Scholar
4Beesack, P. R.. Integral inequalities of the Wirtinger type. Duke Math. J. 25 (1958), 477–498.CrossRefGoogle Scholar
5Benson, D. C.. Inequalities involving integrals of functions and their derivatives. J. Math. Anal. Appl. 17 (1967), 292–308.CrossRefGoogle Scholar
6Cheng, S. S.. Systems-conjugate and focal points of fourth order non-selfadjoint differential equations. Trans. Amer. Math. Soc. 223 (1976), 155–165.CrossRefGoogle Scholar
7Cimmino, G.. Estensione dell’ identità di Picone alla più generale equazione differenziale lineare ordinaria autoaggiunta. Atti Accad. Naz. Lincei Rend. Cl. Sci. Fis. Mat. Natur. 28 (1939), 354–364.Google Scholar
8Coddington, E. A. and Levinson, N.. Theory of Ordinary Differential Equations (New York: McGraw-Hill, 1955).Google Scholar
9Coles, W. J.. A general Wirtinger-type inequality. Duke Math. J. 27 (1960), 133–138.CrossRefGoogle Scholar
10Collatz, L.. Eingewertprobleme und ihre Numerische Behandlung (New York: Chelsea, 1948).Google Scholar
11Coppel, W. A.. Disconjugacy. Lecture Notes in Mathematics 220 (Berlin: Springer, 1971).Google Scholar
12Courant, R. and Hilbert, D.. Methods of Mathematical Physics, Vol. 1 (New York: Interscience, 1953).Google Scholar
13Easwaran, S.. Quadratic functionals of n-th order. Canad. Math. Bull. 19 (1976), 159–167.CrossRefGoogle Scholar
14Eastham, M. S. P.. The Picone identity for selfadjoint differential equations of even order. Mathematika 20 (1973), 197–200.CrossRefGoogle Scholar
15Fan, K., Taussky, O. and Todd, J.. Discrete analogs of inequalities of Wirtinger. Monatsh. Math. 59 (1955), 73–90.CrossRefGoogle Scholar
16Kamke, E.. Über die definiten selbstadjungierten Eigenwertaufgaben bei gewöhnlichen linearen Differentialgleichungen I. Math. Z. 45 (1939), 759–787; II, ibid. 46 (1940), 231–250; III, ibid. 46 (1940), 251–286; IV, ibid, 48 (1942), 67–100.CrossRefGoogle Scholar
17Kreith, K.. Oscillation Theory. Lecture Notes in Mathematics 324 (Berlin: Springer, 1974).Google Scholar
18Leighton, W.. Quadratic functionals of second order. Trans. Amer. Math. Soc. 151 (1970), 309–322.CrossRefGoogle Scholar
19Mikhlin, S. G.. The Problem of the Minimum of a Quadratic Functional (San Francisco: Holden-Day, 1965).Google Scholar
20Nečas, J.. Les Méthodes Directes en Théorie des Équations Elliptiques (Paris: Masson, 1967).Google Scholar
21Reid, W. T.. Ordinary Differential Equations (New York: Wiley, 1971).Google Scholar
22Schmitt, K. and Smith, H. L.. Positive solutions and conjugate points for systems of differential equations. Nonlinear Anal. 2 (1978), 93–105.CrossRefGoogle Scholar
23Swanson, C. A.. Wirtinger's inequality. SIAM J. Math. Anal. 9 (1978), 484–491.CrossRefGoogle Scholar