Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T05:55:41.033Z Has data issue: false hasContentIssue false
  • English
  • Français

Heteroclinic orbits between rotating waves in hyperbolic balance laws

Published online by Cambridge University Press:  14 November 2011

Jörg Härterich
Jörg Härterich
Affiliation:
Freie Universität Berlin, Arnimallee 2-6, D-14195 Berlin, Germany, ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We deal with the large-time behaviour of scalar hyperbolic conservation laws with source terms

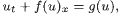
which are often called hyperbolic balance laws. Fan and Hale have proved existence of a global attractor 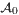for this equation with x ∈ S1. 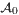consists of spatially homogeneous equilibria, a large number of rotating waves and of heteroclinic orbits between these objects. In this paper, we solve the connection problem and show which equilibria and rotating waves are connected by a heteroclinic orbit. Apart from existence results, our approach via generalized characteristics also gives geometric information about the heteroclinic solutions, e.g. about the shock curves and their strength.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 129 , Issue 3 , 1999 , pp. 519 - 538
Copyright
Copyright © Royal Society of Edinburgh 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Angenent, S. and Fiedler, B.. The dynamics of rotating waves in scalar reaction diffusion equations. Trans. AMS 307 (1988), 545–568.CrossRefGoogle Scholar
2Dafermos, C.. Generalized characteristics and the structure of solutions of hyperbolic conservation laws. Indiana Univ. Math. 26 (1977), 1097–1119.CrossRefGoogle Scholar
3Fan, H. and Hale, J. K.. Large-time behavior in inhomogeneous conservation laws. Arch. Ration. Mech. Analysis 125 (1993), 201–216.CrossRefGoogle Scholar
4Fan, H. and Hale, J. K.. Attractors in inhomogeneous conservation laws and parabolic regularizations. Trans. Am. Math. Soc. 347 (1995), 1239–1254.CrossRefGoogle Scholar
5Härterich, J.. Equilibrium solutions of viscous scalar balance laws with a convex flux. Preprint, Freie Universität Berlin (1997). Nonlin. Diff. Eqns Appl. (In the press.)Google Scholar
6Härterich, J.. Attractors of viscous balance laws: Uniform estimates for the dimension. J. Diff. Eqns 142 (1998), 188–211.CrossRefGoogle Scholar
7Kruzhkov, S. N.. First order quasilinear equations in several independent variables. Math. USSR-Sbornik 10 (1970), 217–243.CrossRefGoogle Scholar
8Lax, P.. Hyperbolic systems of conservation laws. II. Commun. Pure Appl. Math. 10 (1957), 537–566.CrossRefGoogle Scholar
9Lax, P.. Hyperbolic systems of conservation laws and the mathematical theory of shock waves (Philadelphia, PA: SIAM, 1973).CrossRefGoogle Scholar
10Lyberopoulos, A. N.. A Poincaré–Bendixson theorem for scalar balance laws. Proc. R. Soc. Edinb. A 124, (1994), 589–607.CrossRefGoogle Scholar
11Matano, H. and Nakamura, K.-I.. The global attractor of semilinear parabolic equations on S 1. Discr. Cont. Dyn. Systems 3 (1997), 1–24.CrossRefGoogle Scholar
12Sinestrari, C.. Large time behaviour of solutions of balance laws with periodic initial data. Nonlin. Diff. Eqns Appl. 2 (1995), 111–131.CrossRefGoogle Scholar
13Sinestrari, C.. Instabilities of discontinuous travelling waves for hyperbolic balance laws. J. Diff. Eqns 134 (1997), 269–285.CrossRefGoogle Scholar