Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T01:51:01.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat flow with tangent penalisation converging to mean curvature motion

Published online by Cambridge University Press:  14 November 2011

Jian Zhai
Jian Zhai
Affiliation:
Department of Mathematics, Hokkaido University, Sapporo 060, Japan
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove that mean curvature motion can be regarded as the singular limit of the following model:

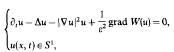
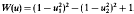where ε > 0 is a small parameter and . This model is related to the Landau–Lifshitz equation of ferromagnetism. Local existence of classical solutions of the Dirichlet problem and global existence of the travelling wave solutions are also obtained.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 4 , 1998 , pp. 875 - 894
Copyright
Copyright © Royal Society of Edinburgh 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bronsard, L. and Kohn, R. V.. Motion by mean curvature as the singular limit of Ginzburg-Landau dynamics. J. Differential Equations 90 (1991), 211–37.CrossRefGoogle Scholar
2Chen, Y.-G., Giga, Y. and Goto, S.. Uniqueness and existence of viscosity solutions of generalized mean curvature flow equations. J. Differential Geom., 33 (1991), 749–86.CrossRefGoogle Scholar
3Crandall, M. G., Ishii, H. and Lions, P. L.. User's guide to viscosity solutions of second order partial differential equations. Bull. Amer. Math. Soc. 27 (1992), 1–67.CrossRefGoogle Scholar
4Evans, L. C., Soner, H. M. and Souganidis, P. E.. Phase transitions and generalized motion by mean curvature. Comm. Pure Appl. Math. 45 (1992), 1097–123.CrossRefGoogle Scholar
5Evans, L. C. and Spruck, J.. Motion of level sets by mean curvature I. J. Differential Geom. 33 (1991), 635–81.CrossRefGoogle Scholar
6Guo, B. and Hong, M-C.. The Landau–Lifshitz equation of the ferromagnetic spin chain and harmonic maps. Calc. Var. 1 (1993), 311–34.Google Scholar
7Hamilton, R.. Harmonic maps of manifolds with boundary, Lecture Notes in Mathematics 471 45 (Berlin: Springer, 1975).CrossRefGoogle Scholar
8Ilmanen, T.. Convergence of the Allen–Cahn equation to Brakke's motion by mean curvature. J. Differential Geom. 38 (1993), 417–61.CrossRefGoogle Scholar
9Ladyzhenskaya, O., Solonnikov, V. and Ural'ceva, N.. Linear and quasilinear equations of parabolic type, Translocations of Mathematical Monographs 23 (Providence, RI: American Mathematical Society, 1968).CrossRefGoogle Scholar
10Ohta, T., Jasnow, D. and Kawasaki, K.. Universal scaling in the motion of random interfaces. Phys. Rev. Lett. 49 (1982), 1223–6.CrossRefGoogle Scholar
11Osher, S. and Sethian, J. A.. Fronts propagating with curvature dependent speed. Algorithms based on Hamilton-Jacobi formations. J. Comput. Phys. 79 (1988), 12–49.CrossRefGoogle Scholar
12Rubinstein, J., Sternberg, P. and Keller, J. B.. Fast reaction, slow diffusion, and curve shortening. SIAM J. Appl. Math. 49 (1989), 116–33.CrossRefGoogle Scholar
13Rubinstein, J., Sternberg, P. and Keller, J. B.. Reaction–diffusion processes and evolution to harmonic map. SIAM J. Appl. Math. 49 (1989), 1722–33.CrossRefGoogle Scholar
14Struwe, M.. On the evolution of harmonic maps of Riemannian surfaces. Comment Math. Helv. 60 (1985), 558–81.CrossRefGoogle Scholar
15Zhai, J.. Heat flow with tangent penalization. Nonlinear Anal, (to appear).Google Scholar