Published online by Cambridge University Press: 14 November 2011
We obtain an explicit formula for the essential norm of a Hankel operator with its symbol in the space PC, which is the closure in L∞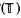 of the space of piecewise continuous functions on the unit circle
of the space of piecewise continuous functions on the unit circle 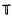 . It follows from this formula that functions in PC can be approximated as closely by functions in C, the continuous functions on the circle, as by functions in the much larger space H∞ + C. This is an example of the way in which properties of the Hardy spaces can be derived from properties of Hankel operators.
. It follows from this formula that functions in PC can be approximated as closely by functions in C, the continuous functions on the circle, as by functions in the much larger space H∞ + C. This is an example of the way in which properties of the Hardy spaces can be derived from properties of Hankel operators.