Half-eigenvalues of elliptic operators
Published online by Cambridge University Press: 12 July 2007
Abstract
Suppose that L is a second-order self-adjoint elliptic partial differential operator on a bounded domain Ω ⊂ Rn, n ≥ 2, and a, b ∈ L∞(Ω). If the equation Lu = au+ − bu− + λu (where λ ∈ R and u±(x) = max{±u(x), 0}) has a non-trivial solution u, then λ is said to be a half-eigenvalue of (L; a, b). In this paper, we obtain some general properties of the half-eigenvalues of (L; a, b) and also show that, generically, the half-eigenvalues are ‘simple’.
We also consider the semilinear problem
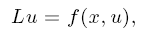 where f : Ω × R → R is a Carathéodory function such that, for a.e. x ∈ Ω,
where f : Ω × R → R is a Carathéodory function such that, for a.e. x ∈ Ω,
 and we relate the solvability properties of this problem to the location of the half-eigenvalues of (L; a, b).
and we relate the solvability properties of this problem to the location of the half-eigenvalues of (L; a, b).
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 132 , Issue 6 , December 2002 , pp. 1439 - 1451
- Copyright
- Copyright © Royal Society of Edinburgh 2002
- 6
- Cited by


