Published online by Cambridge University Press: 14 November 2011
We give here a group extension sequence for calculating, for a non-simply-connected space X, the group of self-homotopy-equivalence classes which induce the identity automorphism of the fundamental group, that is the kernel 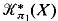 of the representation
of the representation 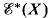 → aut (π1(X)). This group extension sequence gives
→ aut (π1(X)). This group extension sequence gives 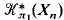 in terms of
in terms of 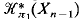 , where Xn is the n-th stage of a Postnikov decomposition. As special cases, we calculate
, where Xn is the n-th stage of a Postnikov decomposition. As special cases, we calculate 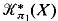 for non-simply-connected spaces having at most two non-trivial homotopy groups, in dimensions 1 and n, as the unit group of a semigroup structure on
for non-simply-connected spaces having at most two non-trivial homotopy groups, in dimensions 1 and n, as the unit group of a semigroup structure on 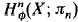 ; and we calculate
; and we calculate 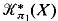 up to extension for non-simply-connected spaces having at most three non-trivial homotopy groups. The group
up to extension for non-simply-connected spaces having at most three non-trivial homotopy groups. The group 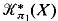 is, for nice spaces, isomorphic to the groups
is, for nice spaces, isomorphic to the groups 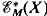 and
and 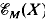 of self-homotopy-equivalence classes of X in the categories top*M and top M, respectively, where X→M = K1(π1(X)) is a top fibration which determines an isomorphism of the fundamental group; and our results are obtained initially in topM.
of self-homotopy-equivalence classes of X in the categories top*M and top M, respectively, where X→M = K1(π1(X)) is a top fibration which determines an isomorphism of the fundamental group; and our results are obtained initially in topM.