No CrossRef data available.
Article contents
Functions with small BMO norm
Published online by Cambridge University Press: 08 January 2025
Abstract
We characterize the functions with ‘small’ bounded mean oscillation (BMO) norm by establishing the precise connection between the space BMO and class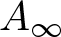 
$A_\infty$ of Muckenhoupt weights. We prove that there exists a universal constant 
$c^*_2$ such that 
$\Vert f \Vert_{BMO} \lt c^*_2$ if and only if 
$\exp f \in A_2$, where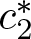 
$c^*_2$ is the sharp constant in the John and Nirenberg inequality. Similarly, in dimension one, we prove that 
$\Vert f \Vert_{BLO} \lt 1$ if and only if 
$\exp f \in A_1$. As application we introduce a structure of metric space in 
$A_\infty$ and prove that the closed unit ball of 
$A_\infty$ is a Banach space.
Keywords
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Coifman, R. R. and Rochberg, R.. Another characterization of BMO. Proc. Am. Math. Soc. 79 (1980), 249–254.CrossRefGoogle Scholar
Dafni, G., Gibara, R. and Lavigne, A.. BMO and the John-Nirenberg inequality on measure spaces. Anal. Geom. Metr. Spaces 8 (2020), 335–362.CrossRefGoogle Scholar
Fefferman, C.. Characterizations of bounded mean oscillation. Bull. Amer. Math. Soc. 77 (1971), 587–588.CrossRefGoogle Scholar
Garcia-Cuerva, J. and Rubio de Francia, J. L.. Weighted norm inequalities and related topics. North-Holland Math. Stud. 116 (1985).Google Scholar
Hytönen, T. and Pérez, C.. Sharp weighted bounds involving 
$A_\infty$. Analysis & PDE 6 (2013), 777–818.CrossRefGoogle Scholar
$A_\infty$. Analysis & PDE 6 (2013), 777–818.CrossRefGoogle ScholarJohn, F. and Nirenberg, L.. On functions of bounded mean oscillation. Comm. Pure Appl. Math. 14 (1961), 415–426.CrossRefGoogle Scholar
Jones, P. W.. Homeomorphisms of the line which preserve BMO. Arkiv för Matematik 21 (1983), 229–231.CrossRefGoogle Scholar
Kinnunen, J. and Shula, P.. The distance of
$L^\infty$ from BMO on metric measure spaces. Adv. Pure Appl. Math. 5 (2014), 117–129.CrossRefGoogle Scholar
$L^\infty$ from BMO on metric measure spaces. Adv. Pure Appl. Math. 5 (2014), 117–129.CrossRefGoogle ScholarKorenovskii, A.. Mean oscillations and equimeasurable rearrangements of functions, Lecture Notes of the Unione Matematica Italiana, Vol. 4 (Springer, Berlin, 2007).Google Scholar
Korey, M. B.. Ideal weights: asymptotically optimal versions of doubling absolute continuity and mean oscillation. J. Fourier Anal. Appl. 4 (1998), 491–519.CrossRefGoogle Scholar
Lerner, A.. The John–Nirenberg inequality with sharp constants. C. R. Acad. Sci. Paris, Ser. I. 351 (2013), 463–466.CrossRefGoogle Scholar
Nielsen, M. and Šikić, H.. Muckenhoupt class weight decomposition and BMO distance to bounded functions. Proc. Edinb. Math. Soc. 62 (2019), 1017–1031.CrossRefGoogle Scholar
Osȩkowski, A.. Sharp estimates for functions of bounded lower oscillation. Bull. Aust. Math. Soc. 87 (2013), 68–81.CrossRefGoogle Scholar
Ou, W.. Near-symmetry in
$A_\infty$ and refined Jones factorization. Proc. Am. Math. Soc. 136 (2008), 3239–3245.CrossRefGoogle Scholar
$A_\infty$ and refined Jones factorization. Proc. Am. Math. Soc. 136 (2008), 3239–3245.CrossRefGoogle ScholarPattakos, N. and Volberg, A.. The Muckenhoupt
$A_\infty$ class as a metric space and continuity of weighted estimates. Math. Res. Lett. 19 (2012), 499–510.CrossRefGoogle Scholar
$A_\infty$ class as a metric space and continuity of weighted estimates. Math. Res. Lett. 19 (2012), 499–510.CrossRefGoogle ScholarPopoli, A.. Limits of the Ap constants. J. Math. Anal. Appl. 478 (2019), 1218–1229.CrossRefGoogle Scholar
Popoli, A.. Homeomorphisms preserving BMO and BLO. Anal. Math. 47 (2021), 893–906.CrossRefGoogle Scholar