We define and prove the existence of free Banach lattices in the category of Banach lattices and contractive lattice homomorphisms, and establish some of their fundamental properties. We give much more detailed results about their structure in the case when there are only a finite number of generators, and give several Banach lattice characterizations of the number of generators being, respectively, one, finite or countable. 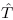We define a Banach lattice P to be projective if, whenever X is a Banach lattice, J is a closed ideal in X, Q : X → X/J is the quotient map, T : P → X/J is a linear lattice homomorphism and ε > 0, there exists a linear lattice homomorphism : P → X such that T = Q º 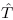and ∥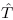∥ ≤ (1 + ε)∥T∥. We establish the connection between projective Banach lattices and free Banach lattices, describe several families of Banach lattices that are projective and prove that some are not.