No CrossRef data available.
Published online by Cambridge University Press: 12 May 2022
In this paper, we establish a new fractional interpolation inequality for radially symmetric measurable functions on the whole space $R^{N}$ and a new compact imbedding result about radially symmetric measurable functions. We show that the best constant in the new interpolation inequality can be achieved by a radially symmetric function. As applications of this compactness result, we study the existence of ground states of the nonlinear fractional Schrödinger equation on the whole space $R^{N}$
and a new compact imbedding result about radially symmetric measurable functions. We show that the best constant in the new interpolation inequality can be achieved by a radially symmetric function. As applications of this compactness result, we study the existence of ground states of the nonlinear fractional Schrödinger equation on the whole space $R^{N}$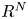 . We also prove an existence result of standing waves and prove their orbital stability.
. We also prove an existence result of standing waves and prove their orbital stability.