Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-28T09:58:56.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Focusing blow-up for quasilinear parabolic equations

Published online by Cambridge University Press:  14 November 2011

C. J. Budd ,
V. A. Galaktionov  and
Jianping Chen
C. J. Budd
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, U.K.
V. A. Galaktionov
Affiliation:
Department of Mathematical Sciences, University of Bath, Bath BA2 7AY, U.K.
Jianping Chen
Affiliation:
Department of Maths and Stats, Simon Fraser University, Burnaby B.C. V5 1S6, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the behaviour of the non-negative blowing up solutions to the quasilinear parabolic equation with a typical reaction–diffusion right-hand side and with a singularity in the space variable which takes the form

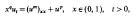
where m ≧ 1, p > 1 are arbitrary constants, in the critical exponent case q = (p–1)/m > 0. We impose zero Dirichlet boundary conditions at the singular point x = 0 and at x = 1, and take large initial data. For a class of ‘concave’ initial functions, we prove focusing at the origin of the solutions as t approaches the blow-up time T in the sense that x = 0 belongs to the blow-up set. The proof is based on an application of the intersection comparison method with an explicit ‘separable’ solution which has the same blow-up time as u. The method has a natural generalisation to the case of more general nonlinearities in the equation. A description of different fine structures of blow-up patterns in the semilinear case m = 1 and in the quasilinear one m > 1 is also presented. A numerical study of the semilinear equation is also made using an adaptive collocation method. This is shown to give very close agreement with the fine structure predicted and allows us to make some conjectures about the general behaviour.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 5 , 1998 , pp. 965 - 992
Copyright
Copyright © Royal Society of Edinburgh 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ad'jutov, M. M. and Lepin, L. A.. Absence of blowing up similarity structures in a medium with a source for constant thermal conductivity. Differentsial'nye Uravneniya 20 (1984), 1279–81 [in Russian].Google Scholar
2Amadori, D.. Unstable blow-up patterns. Differential Integral Equations 8 (1995), 1977–96.CrossRefGoogle Scholar
3Bateman, H. and Erdelyi, E.. Higher Transcendental Functions, vol. 1 (New York: McGraw-Hill, 1953).Google Scholar
4Berbernes, J., Bricher, S. and Galaktionov, V. A.. Asymptotics of blow-up for weakly quasilinear parabolic equations. Nonlinear Anal. 23 (1994), 489–514.CrossRefGoogle Scholar
5Budd, C. J. and Galaktionov, V. A.. Critical diffusion exponents for self-similar blow-up solutions of a quasilinear parabolic equation with an exponential source. Proc. Roy. Soc. Edinburgh Sect. A 126 (1996), 413–41.CrossRefGoogle Scholar
6Budd, C. J., Chen, J., Huang, W. and Russell, R. D.. Moving mesh methods with applications to blow-up problems for PDEs. In Numerical Analysis 1995, Pitman Research Notes in Mathematics 44, pp. 1–18 (Harlow: Longman, 1995).Google Scholar
7Budd, C. J., Dold, B. and Galaktionov, V. A.. Self-similar blow-up for a quasilinear parabolic equation with gradient diffusion and exponential source. Adv. Differential Equations 2 (1997), 85–124.CrossRefGoogle Scholar
8Budd, C. J., Huang, W. and Russell, R. D.. Moving mesh methods for problems with blow-up. SIAM J. Sci. Comp. 17 (1996), 305–27.CrossRefGoogle Scholar
9Dorfi, E. A. and O'c, L.. Drury. Simple adaptive grids for 1-D initial value problems. J. Comput. Phys. 69 (1987), 175–95.CrossRefGoogle Scholar
10Filippas, S. and Kohn, R. V.. Refined asymptotics for the blow-up of ut – ∆u = u p. Comm. Pure Appl. Math. 45 (1992), 821–69.CrossRefGoogle Scholar
11Floater, M. S.. Blow-up at the boundary for degenerate semilinear parabolic equations. Arch. Rational Mech. Anal. 114 (1991), 57–77.CrossRefGoogle Scholar
12Friedman, A. and McLeod, B.. Blow-up of positive solutions of semilinear heat equations. Indiana Univ. Math. J. 34 (1985), 425–47.CrossRefGoogle Scholar
13Galaktionov, V. A.. On asymptotic self-similar behaviour for a quasilinear heat equation: single point blow-up. SIAM J. Math. Anal. 29 (1995), 675–93.CrossRefGoogle Scholar
14Galaktionov, V. A. and Peletier, L. A.. Asymptotic behaviour near finite time extinction for the fast diffusion equation. Arch. Rational Mech. Anal, (to appear).Google Scholar
15Galaktionov, V. A. and Posashkov, S. A.. The equation ut = uxx + u β. Localization, asymptotic behaviour of unbounded solutions (Preprint No. 97, Ketdysh Inst. Appl. Math. Acad. Sci. USSR, Moscow, 1985).Google Scholar
16Galaktionov, V. A. and Posashkov, S. A.. Application of new comparison theorem in the investigation of unbounded solutions of nonlinear parabolic equations. Differential Equations 22 (1986), 809–15.Google Scholar
17Galaktionov, V. A. and Vazquez, J. L.. Extinction for a quasilinear heat equation with absorption II. A dynamical systems approach. Comm. Partial Differential Equations 19 (1994). 1107–37.CrossRefGoogle Scholar
18Giga, Y. and Kohn, R. V.. Asymptotically self-similar blow-up of semilinear heat equations. Comm. Pure Appl. Math. 38 (1985), 297–319.CrossRefGoogle Scholar
19Giga, Y. and Kohn, R. V.. Characterizing blow-up using similarity variables. Indiana Univ. Math. J. 36 (1987), 1–40.CrossRefGoogle Scholar
20Herrero, M. A. and Velazquez, J. J. L.. Blow-up behaviour of one-dimensional semilinear parabolic equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 10 (1993), 131–89.CrossRefGoogle Scholar
21Hocking, L. M., Stuartson, K. and Stuart, J. T.. A non-linear instability burst in plane parallel flow. J. Fluid Mech. 51 (1972), 705–35.CrossRefGoogle Scholar
22Huang, W.-Z. and Russell, R. D. R.. A moving collocation method for solving time dependent partial differential equations. Appl. Numer. Math. 20 (1996), 101–16.CrossRefGoogle Scholar
23Huang, W.-Z.s, Ren, Y. and Russell, R. D. R.. Moving mesh methods based on moving mesh partial differential equations. J. Comput. Phys. 113 (1994), 279–90.CrossRefGoogle Scholar
24Kalashnikov, A. S.. Some problems of the qualitative theory of non-linear degenerate second-order parabolic equations. Russian Math. Surveys 42 (1987), 169–222.CrossRefGoogle Scholar
25Kamin, S. and Rosenau, P.. Non-linear diffusion in a finite mass medium. Comm. Pure Appl. Math. 35 (1982), 113–27.Google Scholar
26Lacey, A. A.. The form of blow-up for nonlinear parabolic equations. Proc. Roy. Soc. Edinburgh Sect. A 98 (1984), 183–202.CrossRefGoogle Scholar
27Ockendon, H.. Channel flows with temperature-dependent viscosity and internal viscous dissipation. J. Fluid Mech. 93 (1979), 737–46.CrossRefGoogle Scholar
28Petzold, L. R.. A description of DASSL: A differential/algebraic system solver (Sandia Natinal Labs. Report SAND82-8637, 1982).Google Scholar
29Pohozaev, S. I.. Eigenfunction of the equation ∆u + ℷf(u) = 0. Soviet Math. Dokl. 6 (1965), 1408–11.Google Scholar
30Richtmyer, R. D.. Principles of Advanced Mathematical Physics, Vol. 1 (Berlin: Springer, 1978).CrossRefGoogle Scholar
31Samarskii, A. A., Galaktionov, V. A., Kurdyumov, S. P. and Mikhailov, A. P.. Blow-up in Quasilinear Parabolic Equations (Moscow: Nauka, 1987 [in Russian]; English translation: Berlin/New York: Walter de Gruyter, 1995).CrossRefGoogle Scholar
32Velázquez, J. J. L., Galaktionov, V. A. and Herrero, M. A.. The space structure near a blow-up point for semilinear heat equations: a formal approach. Zh. Vychisl. Mat. i Mat. Fiz. 31 (1991), 399–411; USSR Comput. Math. Math. Phys. 31 (1991), 3–11.Google Scholar