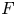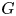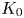1. Introduction
The classical problem of what are the possible homotopy types of fixed sets of cellular group actions on contractible finite CW-complexes was solved by L. Jones [Reference Jones8] in the case of $p$![]() -groups, and R. Oliver [Reference Oliver10] for non-$p$
-groups, and R. Oliver [Reference Oliver10] for non-$p$![]() -groups. Our aim in this paper is to put the work of Oliver into a more general context, exposing where the fundamental group does and where it does not play a role. The analogous generalization of Jones’ work has very different features, which we discuss in the companion paper [Reference Cappell, Weinberger and Yan4].
-groups. Our aim in this paper is to put the work of Oliver into a more general context, exposing where the fundamental group does and where it does not play a role. The analogous generalization of Jones’ work has very different features, which we discuss in the companion paper [Reference Cappell, Weinberger and Yan4].
The following is our original motivation. Suppose $G$![]() is a finite group acting by isometries on a compact Riemannian manifold $X$
is a finite group acting by isometries on a compact Riemannian manifold $X$![]() with non-positive curvature, and the centre of the fundamental group $\pi _1(X)$
with non-positive curvature, and the centre of the fundamental group $\pi _1(X)$![]() is trivial. Then the $G$
is trivial. Then the $G$![]() -action has a fixed point if and only if the induced homomorphism $G\to \text {Out}(\pi _1(X))$
-action has a fixed point if and only if the induced homomorphism $G\to \text {Out}(\pi _1(X))$![]() lifts to $\text {Aut}(\pi _1(X))$
lifts to $\text {Aut}(\pi _1(X))$![]() . Here $\text {Out}(\pi _1(X))$
. Here $\text {Out}(\pi _1(X))$![]() is the group of outer automorphisms, and $\text {Aut}(\pi _1(X))$
is the group of outer automorphisms, and $\text {Aut}(\pi _1(X))$![]() is the group of genuine automorphisms. By taking the fundamental group to be based at a fixed point, we see the lift is necessary. The sufficiency of the condition follows by considering the group $\Gamma$
is the group of genuine automorphisms. By taking the fundamental group to be based at a fixed point, we see the lift is necessary. The sufficiency of the condition follows by considering the group $\Gamma$![]() of lifts of $G$
of lifts of $G$![]() to the universal cover. Since the centre of $\pi _1(X)$
to the universal cover. Since the centre of $\pi _1(X)$![]() is trivial, the map $\Gamma \to G$
is trivial, the map $\Gamma \to G$![]() splits. By Cartan's fixed point theorem [Reference Bridson and Haefliger3], any finite group of isometries of a simply connected non-positively curved manifold has a fixed point.
splits. By Cartan's fixed point theorem [Reference Bridson and Haefliger3], any finite group of isometries of a simply connected non-positively curved manifold has a fixed point.
If the action is not required to be by isometries, would the action still have a fixed point? For a $p$![]() -group acting on a finite $K(\pi,1)$
-group acting on a finite $K(\pi,1)$![]() CW-complex with centreless $\pi$
CW-complex with centreless $\pi$![]() , Smith theory implies that any action satisfying the lifting condition must have a fixed point.
, Smith theory implies that any action satisfying the lifting condition must have a fixed point.
What about actions by a non-$p$![]() -group?
-group?
Theorem 1.1 For any finite group $G$![]() of not prime power order, there is a $G$
of not prime power order, there is a $G$![]() -action on some compact aspherical manifold $X$
-action on some compact aspherical manifold $X$![]() , with centreless $\pi =\pi _1(X)$
, with centreless $\pi =\pi _1(X)$![]() , such that the induced homomorphism $G\to \text {Out}(\pi _1(X))$
, such that the induced homomorphism $G\to \text {Out}(\pi _1(X))$![]() lifts to $\text {Aut}(\pi _1(X))$
lifts to $\text {Aut}(\pi _1(X))$![]() , and yet the action has no fixed point.
, and yet the action has no fixed point.
This result uses the method of Davis [Reference Davis5], which promotes constructions involving finite CW-complexes and compact aspherical manifolds with boundary to closed aspherical manifolds. Consequently, we were led to investigate the role of the fundamental group in generalizing the theory of Oliver. In [Reference Cappell, Weinberger and Yan4], we will see a contrastingly different role in generalizing the theory of Jones.
It would be reasonable to believe that $\pi _1(X)$![]() plays a role in understanding the possible fixed sets of group actions on $X$
plays a role in understanding the possible fixed sets of group actions on $X$![]() . In both [Reference Jones8, Reference Oliver10], at key points in the construction, an obstruction in $\widetilde {K}_0({\mathbb {Z}}[G])$
. In both [Reference Jones8, Reference Oliver10], at key points in the construction, an obstruction in $\widetilde {K}_0({\mathbb {Z}}[G])$![]() arises, and one would expect that for non-simply connected $X$
arises, and one would expect that for non-simply connected $X$![]() , an analogous element of $\widetilde {K}_0({\mathbb {Z}}[\Gamma ])$
, an analogous element of $\widetilde {K}_0({\mathbb {Z}}[\Gamma ])$![]() arises. However, in this paper, we shall see that the fundamental group does not intervene in this way for non-$p$
arises. However, in this paper, we shall see that the fundamental group does not intervene in this way for non-$p$![]() -groups (though, as we shall see, it does affect the possible trade-offs between Euler characteristics of different components of fixed points). On the other hand, we shall see in [Reference Cappell, Weinberger and Yan4] that this is the case for $p$
-groups (though, as we shall see, it does affect the possible trade-offs between Euler characteristics of different components of fixed points). On the other hand, we shall see in [Reference Cappell, Weinberger and Yan4] that this is the case for $p$![]() -groups.
-groups.
We begin with some definitions. We say that a $G$![]() -map $f\colon X \to Y$
-map $f\colon X \to Y$![]() between two finite $G$
between two finite $G$![]() -CW-complexes is a pseudo-equivalence if it is an unequivariant homotopy equivalence. The pseudo-equivalence property is equivalent to requiring that the induced map $X\times EG\to Y\times EG$
-CW-complexes is a pseudo-equivalence if it is an unequivariant homotopy equivalence. The pseudo-equivalence property is equivalent to requiring that the induced map $X\times EG\to Y\times EG$![]() on the Borel constructions is a $G$
on the Borel constructions is a $G$![]() -homotopy equivalence. Note that $X\times EG\to X$
-homotopy equivalence. Note that $X\times EG\to X$![]() is a $G$
is a $G$![]() -map and an unequivariant homotopy equivalence. However, the Borel construction is usually not a finite CW-complex, so that the map is not a pseudo-equivalence in the sense of the present paper.
-map and an unequivariant homotopy equivalence. However, the Borel construction is usually not a finite CW-complex, so that the map is not a pseudo-equivalence in the sense of the present paper.
A pseudo-equivalent $G$![]() -map does not necessarily have an inverse pseudo-equivalent $G$
-map does not necessarily have an inverse pseudo-equivalent $G$![]() -map. To make pseudo-equivalence into an equivalence relation, therefore, we need to allow two finite $G$
-map. To make pseudo-equivalence into an equivalence relation, therefore, we need to allow two finite $G$![]() -CW-complexes $X,Y$
-CW-complexes $X,Y$![]() to be pseudo-equivalent if they are related by a zig-zag sequence of pseudo-equivalent $G$
to be pseudo-equivalent if they are related by a zig-zag sequence of pseudo-equivalent $G$![]() -maps (all $Z_i,W_i$
-maps (all $Z_i,W_i$![]() are finite $G$
are finite $G$![]() -CW-complexes)
-CW-complexes)
Then for any $p$![]() -subgroup $P$
-subgroup $P$![]() of $G$
of $G$![]() , the Smith theory [Reference Smith17] can be applied to the fixed sets of $P$
, the Smith theory [Reference Smith17] can be applied to the fixed sets of $P$![]() to give $H_*(X^P;{\mathbb {F}}_p)\cong H_*(Y^P;{\mathbb {F}}_p)$
to give $H_*(X^P;{\mathbb {F}}_p)\cong H_*(Y^P;{\mathbb {F}}_p)$![]() . In particular, this implies that, if a $p$
. In particular, this implies that, if a $p$![]() -group $G$
-group $G$![]() acts freely on $X$
acts freely on $X$![]() , then the $G$
, then the $G$![]() -action on $Y$
-action on $Y$![]() must also be free. If we allowed infinite CW-complexes in our definition, we could not make this assertion as $EG\to *$
must also be free. If we allowed infinite CW-complexes in our definition, we could not make this assertion as $EG\to *$![]() would be a pseudo-equivalence.
would be a pseudo-equivalence.
If $G$![]() is not a $p$
is not a $p$![]() -group, however, it is still possible for $X$
-group, however, it is still possible for $X$![]() to have no $G$
to have no $G$![]() -fixed point, and for $Y$
-fixed point, and for $Y$![]() to have $G$
to have $G$![]() -fixed point. For the case $Y$
-fixed point. For the case $Y$![]() is a single point, i.e., $X$
is a single point, i.e., $X$![]() is contractible, Oliver [Reference Oliver10] proved the following.
is contractible, Oliver [Reference Oliver10] proved the following.
Theorem (Oliver): For any finite group $G$![]() of not prime power order, there is a number $n(G)$
of not prime power order, there is a number $n(G)$![]() , such that a contractible finite CW-complexes $F$
, such that a contractible finite CW-complexes $F$![]() is (homotopy equivalent to) the fixed set of a finite contractible $G$
is (homotopy equivalent to) the fixed set of a finite contractible $G$![]() -CW-complex, if and only if $\chi (F)=1$
-CW-complex, if and only if $\chi (F)=1$![]() mod $n(G)$
mod $n(G)$![]() .
.
By [Reference Oliver10, theorem 5] and the subsequent corollary, we know $n(G)=1$![]() , i.e., there is no condition at all on $F$
, i.e., there is no condition at all on $F$![]() , if and only if $G$
, if and only if $G$![]() is not of the form $P\lhd H\lhd G$
is not of the form $P\lhd H\lhd G$![]() , with $P$
, with $P$![]() and $G/H$
and $G/H$![]() having prime power orders, and $H/P$
having prime power orders, and $H/P$![]() cyclic. For example, for $G$
cyclic. For example, for $G$![]() a non-solvable group or an abelian group with at least three non-cyclic Sylow subgroups, we have $n(G)=1$
a non-solvable group or an abelian group with at least three non-cyclic Sylow subgroups, we have $n(G)=1$![]() .
.
We also know $n(G)=0$![]() , i.e., the obstruction is exactly the Euler characteristic, if and only if $G$
, i.e., the obstruction is exactly the Euler characteristic, if and only if $G$![]() has a normal subgroup $P$
has a normal subgroup $P$![]() of prime power order, such that $G/P$
of prime power order, such that $G/P$![]() is cyclic. In particular, a cyclic group has $n(G)=0$
is cyclic. In particular, a cyclic group has $n(G)=0$![]() .
.
For the complete determination of $n(G)$![]() , see [Reference Oliver12, Reference Oliver13].
, see [Reference Oliver12, Reference Oliver13].
The following is our extension of Oliver's theorem to general $Y$![]() .
.
Theorem 1.2 Suppose $G$![]() is a group of not prime power order, and $Y$
is a group of not prime power order, and $Y$![]() is a finite $G$
is a finite $G$![]() -CW-complex with non-empty and connected fixed set $Y^G$
-CW-complex with non-empty and connected fixed set $Y^G$![]() . Then a finite CW-complex $F$
. Then a finite CW-complex $F$![]() is the fixed set of a finite $G$
is the fixed set of a finite $G$![]() -CW-complex pseudo-equivalent to $Y$
-CW-complex pseudo-equivalent to $Y$![]() if and only if $\chi (F)=\chi (Y^G)$
if and only if $\chi (F)=\chi (Y^G)$![]() mod $n(G)$
mod $n(G)$![]() .
.
Remark 1.3 Given the Euler characteristic condition, we actually construct a finite $G$![]() -CW-complex $X$
-CW-complex $X$![]() and a pseudo-equivalence $X\to Y$
and a pseudo-equivalence $X\to Y$![]() , such that $F=X^G$
, such that $F=X^G$![]() . In particular, there is no need to use a zig-zag sequence of maps for the pseudo-equivalence between $X$
. In particular, there is no need to use a zig-zag sequence of maps for the pseudo-equivalence between $X$![]() and $Y$
and $Y$![]() .
.
Oliver introduces another number $m(G)$![]() . This number is the largest square-free factor of $n(G)$
. This number is the largest square-free factor of $n(G)$![]() ; it is the number for which the congruence $\chi (F) = 1$
; it is the number for which the congruence $\chi (F) = 1$![]() mod $m(G)$
mod $m(G)$![]() follows directly from the combination of the Lefshetz theorem and Smith theory. The extra divisibility by $n(G)$
follows directly from the combination of the Lefshetz theorem and Smith theory. The extra divisibility by $n(G)$![]() in Oliver's theorem above for finite $G$
in Oliver's theorem above for finite $G$![]() -CW complexes comes from deeper algebraic $K$
-CW complexes comes from deeper algebraic $K$![]() -theory considerations. As shown in [Reference Quinn15, § 2], this arises in answering the question about fixed sets of compact $G$
-theory considerations. As shown in [Reference Quinn15, § 2], this arises in answering the question about fixed sets of compact $G$![]() -ANRs (equivariant absolute neighbourhood retracts) that are not necessarily homotopy finite.Footnote 1 The same method, combined with the arguments of the present paper, proves the $G$
-ANRs (equivariant absolute neighbourhood retracts) that are not necessarily homotopy finite.Footnote 1 The same method, combined with the arguments of the present paper, proves the $G$![]() -ANR analogues of all our results, with $m(G)$
-ANR analogues of all our results, with $m(G)$![]() replacing $n(G)$
replacing $n(G)$![]() . Such results are relevant to locally linear group actions on topological manifolds. The following is the $G$
. Such results are relevant to locally linear group actions on topological manifolds. The following is the $G$![]() -ANR analogue of theorem 1.2. Of course, the statement requires us to slightly extend pseudo-equivalence to the compact $G$
-ANR analogue of theorem 1.2. Of course, the statement requires us to slightly extend pseudo-equivalence to the compact $G$![]() -ANR category.
-ANR category.
Theorem 1.4 Suppose $G$![]() is a group of not prime power order, and $Y$
is a group of not prime power order, and $Y$![]() is a compact $G$
is a compact $G$![]() -ANR with non-empty and connected fixed set $Y^G$
-ANR with non-empty and connected fixed set $Y^G$![]() . Then a finite CW-complex $F$
. Then a finite CW-complex $F$![]() is the fixed set of a compact $G$
is the fixed set of a compact $G$![]() -ANR pseudo-equivalent to $Y$
-ANR pseudo-equivalent to $Y$![]() if and only if $\chi (F)=\chi (Y^G)$
if and only if $\chi (F)=\chi (Y^G)$![]() mod $m(G)$
mod $m(G)$![]() .
.
An interesting class of actions is pseudo-trivial action, which means a finite $G$![]() -CW-complex $X$
-CW-complex $X$![]() equivariantly homotopy equivalent to $X$
equivariantly homotopy equivalent to $X$![]() with trivial action. This is tantamount to saying that the G-map $X\to X/G$
with trivial action. This is tantamount to saying that the G-map $X\to X/G$![]() splits. Any action on a contractible CW-complex is pseudo-trivial. These actions frequently arise as $G$
splits. Any action on a contractible CW-complex is pseudo-trivial. These actions frequently arise as $G$![]() -subspaces of more general $G$
-subspaces of more general $G$![]() -spaces, and their analysis is important for inductive arguments. Indeed this is implicit in the proof of our theorem 1.7 below, and is also used in solving our motivating problem about aspherical manifolds.
-spaces, and their analysis is important for inductive arguments. Indeed this is implicit in the proof of our theorem 1.7 below, and is also used in solving our motivating problem about aspherical manifolds.
If we apply theorem 1.2 to the case the action on $Y$![]() is trivial, we find that $F$
is trivial, we find that $F$![]() is the fixed set of a pseudo-trivial, finite $G$
is the fixed set of a pseudo-trivial, finite $G$![]() -CW-complex homotopy equivalent to $Y$
-CW-complex homotopy equivalent to $Y$![]() if and only if $\chi (F)=\chi (Y)$
if and only if $\chi (F)=\chi (Y)$![]() mod $n(G)$
mod $n(G)$![]() .
.
The fundamental group does not appear in theorem 1.2. However, there is an important role for the fundamental group when $Y^G$![]() is not connected. The fundamental group and the action group interact as follows: As before, let $\Gamma$
is not connected. The fundamental group and the action group interact as follows: As before, let $\Gamma$![]() be the group of liftings of $G$
be the group of liftings of $G$![]() -actions on $Y$
-actions on $Y$![]() to the universal cover $\widetilde {Y}$
to the universal cover $\widetilde {Y}$![]() . We have an exact sequence, with some modification needed if the action is not effective [see discussion after (6.1)],
. We have an exact sequence, with some modification needed if the action is not effective [see discussion after (6.1)],
If $\widetilde {y}\in \widetilde {Y}$![]() covers $y\in Y$
covers $y\in Y$![]() , then we have isomorphism of isotropy groups $\Gamma _{\widetilde {y}}\cong G_y$
, then we have isomorphism of isotropy groups $\Gamma _{\widetilde {y}}\cong G_y$![]() . For $y\in Y^G$
. For $y\in Y^G$![]() , this gives a splitting of the exact sequence. Various choices of $\widetilde {y}$
, this gives a splitting of the exact sequence. Various choices of $\widetilde {y}$![]() over $y$
over $y$![]() give a conjugacy class of splittings, and the conjugacy class depends only on the connected component of $Y^G$
give a conjugacy class of splittings, and the conjugacy class depends only on the connected component of $Y^G$![]() containing $y$
containing $y$![]() .
.
To see the interaction of $G$![]() with $\pi _1(Y)$
with $\pi _1(Y)$![]() at the level of fixed sets, we introduce the following definition.
at the level of fixed sets, we introduce the following definition.
Definition A $G$![]() -action on $Y$
-action on $Y$![]() is weakly $G$
is weakly $G$![]() -connected if each connected component of $Y^G$
-connected if each connected component of $Y^G$![]() corresponds to a different conjugacy class of lifts of $G$
corresponds to a different conjugacy class of lifts of $G$![]() to $\Gamma$
to $\Gamma$![]() .
.
Recall that a $G$![]() -space $Y$
-space $Y$![]() is said to be $G$
is said to be $G$![]() -connected, if $Y^H$
-connected, if $Y^H$![]() is non-empty and connected for every subgroup $H$
is non-empty and connected for every subgroup $H$![]() of $G$
of $G$![]() . Evidently, $G$
. Evidently, $G$![]() -connected implies weakly $G$
-connected implies weakly $G$![]() -connected, but the converse is often false. For example, a free action is weakly $G$
-connected, but the converse is often false. For example, a free action is weakly $G$![]() -connected but not $G$
-connected but not $G$![]() -connected. Another example is actions by isometries on non-positively curved spaces, again by Cartan's fixed point theorem.
-connected. Another example is actions by isometries on non-positively curved spaces, again by Cartan's fixed point theorem.
Theorem 1.5 Suppose $G$![]() is a cyclic group or more generally satisfies $n(G)=0$
is a cyclic group or more generally satisfies $n(G)=0$![]() , $F$
, $F$![]() is a finite CW-complex, and $Y$
is a finite CW-complex, and $Y$![]() is a finite $G$
is a finite $G$![]() -CW-complex. If $Y$
-CW-complex. If $Y$![]() is weakly $G$
is weakly $G$![]() -connected, then a $G$
-connected, then a $G$![]() -map $f\colon F\to Y$
-map $f\colon F\to Y$![]() can be extended to a pseudo-equivalence $g\colon X\to Y$
can be extended to a pseudo-equivalence $g\colon X\to Y$![]() , with $X$
, with $X$![]() a finite $G$
a finite $G$![]() -CW-complex satisfying $F=X^G$
-CW-complex satisfying $F=X^G$![]() , if and only if for each connected component $C$
, if and only if for each connected component $C$![]() of $Y^G$
of $Y^G$![]() , we have $\chi (f^{-1}(C))=\chi (C)$
, we have $\chi (f^{-1}(C))=\chi (C)$![]() .
.
As in [Reference Cappell, Weinberger and Yan4], we call $g\colon X\to Y$![]() a pseudo-equivalence extension of $f\colon F\to Y$
a pseudo-equivalence extension of $f\colon F\to Y$![]() . Specifically, in such an extension, we require all spaces to be finite $G$
. Specifically, in such an extension, we require all spaces to be finite $G$![]() -CW-complexes (unless otherwise stated), and $F=X^G$
-CW-complexes (unless otherwise stated), and $F=X^G$![]() .
.
Since connected $Y^G$![]() implies weakly $G$
implies weakly $G$![]() -connected, theorem 1.5 generalizes theorem 1.2 in case $n(G)=0$
-connected, theorem 1.5 generalizes theorem 1.2 in case $n(G)=0$![]() .
.
The theorem allows $f^{-1}(C)=\emptyset$![]() for some connected components. It also allows $f^{-1}(C)$
for some connected components. It also allows $f^{-1}(C)$![]() to be disconnected for some connected component $C$
to be disconnected for some connected component $C$![]() . Then $X$
. Then $X$![]() will no longer be weakly $G$
will no longer be weakly $G$![]() -connected, but our weakly $G$
-connected, but our weakly $G$![]() -connected hypothesis is on $Y$
-connected hypothesis is on $Y$![]() . Our proof of the theorem uses the Hattori–Stallings trace [Reference Bass2, Reference Hattori7, Reference Stallings18], perhaps the most classical of the trace maps from $K$
. Our proof of the theorem uses the Hattori–Stallings trace [Reference Bass2, Reference Hattori7, Reference Stallings18], perhaps the most classical of the trace maps from $K$![]() -theory to Hochschild (or even cyclic) homology.
-theory to Hochschild (or even cyclic) homology.
Even without the weakly $G$![]() -connected assumption, our methods apply to give some new constructions of actions, and some new necessary congruence conditions. In this general setting, our results can be profitably compared to earlier work of Oliver and Petrie [Reference Oliver and Petrie14] (which deals with a somewhat different problem) and Morimoto and Iizuka [Reference Morimoto and Iizuka9] (which is about pseudo-equivalence of $G$
-connected assumption, our methods apply to give some new constructions of actions, and some new necessary congruence conditions. In this general setting, our results can be profitably compared to earlier work of Oliver and Petrie [Reference Oliver and Petrie14] (which deals with a somewhat different problem) and Morimoto and Iizuka [Reference Morimoto and Iizuka9] (which is about pseudo-equivalence of $G$![]() -CW-complexes with finite fundamental groups).
-CW-complexes with finite fundamental groups).
Theorem 1.6 Suppose $G$![]() is a finite group of not prime power order, and $Y$
is a finite group of not prime power order, and $Y$![]() is a finite $G$
is a finite $G$![]() -CW-complex. Then there is a subgroup $N(Y)$
-CW-complex. Then there is a subgroup $N(Y)$![]() of ${\mathbb {Z}}^{\pi _0Y^G}$
of ${\mathbb {Z}}^{\pi _0Y^G}$![]() , such that a $G$
, such that a $G$![]() -map $f\colon F\to Y$
-map $f\colon F\to Y$![]() from a finite CW-complex $F$
from a finite CW-complex $F$![]() with trivial $G$
with trivial $G$![]() -action has pseudo-equivalence extension, if and only if
-action has pseudo-equivalence extension, if and only if
For $f\colon F\to Y$![]() to have pseudo-equivalence extension $g\colon X\to Y$
to have pseudo-equivalence extension $g\colon X\to Y$![]() , it is necessary that the global Euler characteristic condition $\chi (F)=\chi (Y^G)$
, it is necessary that the global Euler characteristic condition $\chi (F)=\chi (Y^G)$![]() mod $n(G)$
mod $n(G)$![]() is satisfied. The reason is that the mapping cone $cX\cup _g Y$
is satisfied. The reason is that the mapping cone $cX\cup _g Y$![]() of the homotopy equivalence $g$
of the homotopy equivalence $g$![]() is a contractible $G$
is a contractible $G$![]() -CW-complex with fixed set $(cX\cup _g Y)^G=cF\cup Y^G$
-CW-complex with fixed set $(cX\cup _g Y)^G=cF\cup Y^G$![]() . Then Oliver's theorem implies $\chi (cF\cup Y^G)=1+\chi (Y^G)-\chi (F)=1$
. Then Oliver's theorem implies $\chi (cF\cup Y^G)=1+\chi (Y^G)-\chi (F)=1$![]() mod $n(G)$
mod $n(G)$![]() .
.
Conversely, the following result says that, if the local Euler characteristic condition is satisfied for each connected component of $Y^G$![]() , then we have the pseudo-equivalence extension.
, then we have the pseudo-equivalence extension.
Theorem 1.7 Suppose $G$![]() is a group of not prime power order, $F$
is a group of not prime power order, $F$![]() is a finite CW-complex with trivial $G$
is a finite CW-complex with trivial $G$![]() -action, $Y$
-action, $Y$![]() is a connected finite $G$
is a connected finite $G$![]() -CW-complex, and $f\colon F\to Y$
-CW-complex, and $f\colon F\to Y$![]() is a $G$
is a $G$![]() -map. If $\chi (f^{-1}(C))=\chi (C)$
-map. If $\chi (f^{-1}(C))=\chi (C)$![]() mod $n(G)$
mod $n(G)$![]() for every connected component $C$
for every connected component $C$![]() of $Y^G$
of $Y^G$![]() , then $f$
, then $f$![]() has pseudo-equivalence extension.
has pseudo-equivalence extension.
The discussion on global versus local Euler characteristic conditions means exactly that the group $N(Y)$![]() introduced in theorem 1.6 satisfies
introduced in theorem 1.6 satisfies
We note two cases in which the two bounds for $N(Y)$![]() coincide. If $Y^G$
coincide. If $Y^G$![]() is connected, then $N(Y)=n(G){\mathbb {Z}}$
is connected, then $N(Y)=n(G){\mathbb {Z}}$![]() , and we recover theorem 1.2. If $n(G)=1$
, and we recover theorem 1.2. If $n(G)=1$![]() , then $N(Y)={\mathbb {Z}}^A$
, then $N(Y)={\mathbb {Z}}^A$![]() , which means there is no obstruction at all.
, which means there is no obstruction at all.
Under the condition of theorem 1.5, we know $N(Y)$![]() is the lower bound $n(G){\mathbb {Z}}^A$
is the lower bound $n(G){\mathbb {Z}}^A$![]() , i.e., the local Euler characteristic condition is sufficient. To get a somewhat non-trivial example where $N(Y)$
, i.e., the local Euler characteristic condition is sufficient. To get a somewhat non-trivial example where $N(Y)$![]() is isomorphic to the upper bound, we consider a finite contractible $G$
is isomorphic to the upper bound, we consider a finite contractible $G$![]() -CW-complex $Y$
-CW-complex $Y$![]() , and any $G$
, and any $G$![]() -map $f\colon F\to Y$
-map $f\colon F\to Y$![]() satisfying the global Euler characteristic condition $\chi (F)=\chi (Y^G)=1$
satisfying the global Euler characteristic condition $\chi (F)=\chi (Y^G)=1$![]() mod $n(G)$
mod $n(G)$![]() . By Oliver's theory [Reference Oliver10], there is a finite contractible $G$
. By Oliver's theory [Reference Oliver10], there is a finite contractible $G$![]() -CW-complex $X$
-CW-complex $X$![]() , such that $F=X^G$
, such that $F=X^G$![]() . If we extend $f\colon F\to Y$
. If we extend $f\colon F\to Y$![]() to a $G$
to a $G$![]() -map $g\colon X\to Y$
-map $g\colon X\to Y$![]() , then $g$
, then $g$![]() is a pseudo-equivalence due to the contractibility of $X$
is a pseudo-equivalence due to the contractibility of $X$![]() and $Y$
and $Y$![]() . The extension exists as long as all the fixed sets $Y^H$
. The extension exists as long as all the fixed sets $Y^H$![]() are sufficiently highly connected. There is a $G$
are sufficiently highly connected. There is a $G$![]() -representation $V$
-representation $V$![]() , such that the representation sphere $S(V)$
, such that the representation sphere $S(V)$![]() has no fixed point by $G$
has no fixed point by $G$![]() , and is highly connected for the fixed sets of proper subgroups (see the first remark after the proof of lemma 4.2). Then $Z=Y*S(V)$
, and is highly connected for the fixed sets of proper subgroups (see the first remark after the proof of lemma 4.2). Then $Z=Y*S(V)$![]() is still contractible, and satisfies $Z^G=Y^G$
is still contractible, and satisfies $Z^G=Y^G$![]() . Moreover, $Z$
. Moreover, $Z$![]() becomes highly connected for the fixed sets of proper subgroups. The contractibility implies that the natural map $h\colon Y\to Z$
becomes highly connected for the fixed sets of proper subgroups. The contractibility implies that the natural map $h\colon Y\to Z$![]() is a pseudo-equivalence. Therefore, $h\circ f\colon F\to Z$
is a pseudo-equivalence. Therefore, $h\circ f\colon F\to Z$![]() can be extended to a pseudo-equivalent $G$
can be extended to a pseudo-equivalent $G$![]() -map $g\colon X\to Z$
-map $g\colon X\to Z$![]() .
.
In general, we have not yet completely ascertained the pattern which determines where between the two given extremes $N(Y)$![]() actually is, although one can easily produce examples where either extreme is realized.
actually is, although one can easily produce examples where either extreme is realized.
Remark 1.8 That being said, if $Y^G=\emptyset$![]() , then it is impossible to construct a pseudo-equivalent action with non-empty fixed set in the context of this paper. However, using zig-zag compositions of pseudo-equivalence maps, sometimes, but not always, it is possible to get from such an action to one whose fixed set is arbitrary.
, then it is impossible to construct a pseudo-equivalent action with non-empty fixed set in the context of this paper. However, using zig-zag compositions of pseudo-equivalence maps, sometimes, but not always, it is possible to get from such an action to one whose fixed set is arbitrary.
Our results about finite $G$![]() -CW-complexes (and compact $G$
-CW-complexes (and compact $G$![]() -ANRs) apply to compact Lie group actions, as well. In [Reference Oliver11], Oliver extended his theorem to the case $G$
-ANRs) apply to compact Lie group actions, as well. In [Reference Oliver11], Oliver extended his theorem to the case $G$![]() is a compact Lie group. He calls $G$
is a compact Lie group. He calls $G$![]() $p$
$p$![]() -toral if the identity component $G_0$
-toral if the identity component $G_0$![]() is a torus, and $G/G_0$
is a torus, and $G/G_0$![]() is a $p$
is a $p$![]() -group. This is precisely the case Smith theory applies. Then Oliver's (and Quinn's) results apply to his problem in the case when $G$
-group. This is precisely the case Smith theory applies. Then Oliver's (and Quinn's) results apply to his problem in the case when $G$![]() is not $p$
is not $p$![]() -toral, for any prime $p$
-toral, for any prime $p$![]() . This means two possibilities: (1) if $G/G_0$
. This means two possibilities: (1) if $G/G_0$![]() is not of prime power order and $G_0$
is not of prime power order and $G_0$![]() is a torus, then the results for $G$
is a torus, then the results for $G$![]() are the same as those for $G/G_0$
are the same as those for $G/G_0$![]() ; (2) if $G_0$
; (2) if $G_0$![]() is not a torus, then we have $n(G)=1$
is not a torus, then we have $n(G)=1$![]() , and there is no Euler characteristic obstruction to making fixed sets. By the direct geometric arguments in § 3 and 4, this also holds in our general setting.
, and there is no Euler characteristic obstruction to making fixed sets. By the direct geometric arguments in § 3 and 4, this also holds in our general setting.
The paper is organized as follows. In § 2 and 3, we prove theorem 1.7 for the case all $F_C=f^{-1}(C)$![]() are not empty. The case some $F_C=\emptyset$
are not empty. The case some $F_C=\emptyset$![]() requires separate treatment, and we prove this case in § 4. This completes the proof of theorem 1.7. Theorem 1.2 immediately follows from theorem 1.7. The special case $F_C=\emptyset$
requires separate treatment, and we prove this case in § 4. This completes the proof of theorem 1.7. Theorem 1.2 immediately follows from theorem 1.7. The special case $F_C=\emptyset$![]() is geometrically significant because it gives actions without fixed points. In fact, we also prove theorem 1.1 in § 4.
is geometrically significant because it gives actions without fixed points. In fact, we also prove theorem 1.1 in § 4.
In § 5, we use a formal construction and theorem 1.7 to prove theorem 1.6. In § 6, we prove two results that give necessary conditions on the Euler characteristics. Theorem 6.2 is for rational pseudo-equivalence under a cyclic group action. Theorem 6.3 is for pseudo-equivalence under the action by a group satisfying $n(G)=0$![]() . Theorem 1.5 is a consequence of the two theorems.
. Theorem 1.5 is a consequence of the two theorems.
We would like to thank K. Pawałowski, R. Oliver and M. Morimoto for valuable conversations about this work. We would also like to thank the referee for suggesting a number of improvements to the exposition.
2. Cell-wise partition of Euler characteristic
The proof of theorem 1.7 starts with the observation that we can inductively apply Oliver's construction to cells of $Y^G$![]() . Recall that a CW-complex $Y$
. Recall that a CW-complex $Y$![]() is regular if every cell $\sigma$
is regular if every cell $\sigma$![]() is given by an embedding $D^k\to Y$
is given by an embedding $D^k\to Y$![]() . This implies that the boundary $\partial \sigma$
. This implies that the boundary $\partial \sigma$![]() of the cell is a sphere $S^{k-1}$
of the cell is a sphere $S^{k-1}$![]() embedded in $Y$
embedded in $Y$![]() . Then $\chi (\sigma )=\chi (D^{\dim \sigma })=1$
. Then $\chi (\sigma )=\chi (D^{\dim \sigma })=1$![]() , and $\chi (\partial \sigma )=\chi (S^{\dim \sigma -1})=1-(-1)^{\dim \sigma }$
, and $\chi (\partial \sigma )=\chi (S^{\dim \sigma -1})=1-(-1)^{\dim \sigma }$![]() .
.
Lemma 2.1 Suppose $Y$![]() is a finite CW-complex, and $f\colon F\to Y$
is a finite CW-complex, and $f\colon F\to Y$![]() is a map. If $\chi (f^{-1}(\sigma ))=1$
is a map. If $\chi (f^{-1}(\sigma ))=1$![]() mod $n$
mod $n$![]() for every cell $\sigma$
for every cell $\sigma$![]() of $Y$
of $Y$![]() , then $\chi (F)=\chi (Y)$
, then $\chi (F)=\chi (Y)$![]() mod $n$
mod $n$![]() .
.
The lemma allows $n=0$![]() , which means dropping ‘mod $n$
, which means dropping ‘mod $n$![]() ’ in the statement. In the following proof, all Euler characteristic equalities are true mod $n$
’ in the statement. In the following proof, all Euler characteristic equalities are true mod $n$![]() .
.
Proof. If $\dim Y=0$![]() , then $Y$
, then $Y$![]() consists of finitely many points $y_1,y_2,\dots,y_k$
consists of finitely many points $y_1,y_2,\dots,y_k$![]() , and $F=\cup _{i=1}^k f^{-1}(y_i)$
, and $F=\cup _{i=1}^k f^{-1}(y_i)$![]() is a disjoint union. By the assumption, we have $\chi (f^{-1}(y_i))=1$
is a disjoint union. By the assumption, we have $\chi (f^{-1}(y_i))=1$![]() . Therefore, $\chi (F)=\sum _{i=1}^k \chi (f^{-1}(y_i))=k=\chi (Y)$
. Therefore, $\chi (F)=\sum _{i=1}^k \chi (f^{-1}(y_i))=k=\chi (Y)$![]() .
.
Suppose $\dim Y=d$![]() , and the lemma is proved for finite CW-complexes of dimension $< d$
, and the lemma is proved for finite CW-complexes of dimension $< d$![]() . We have $Y^{d-1}=Y_0\subset Y_1\subset \cdots \subset Y_{k-1}\subset Y_k=Y$
. We have $Y^{d-1}=Y_0\subset Y_1\subset \cdots \subset Y_{k-1}\subset Y_k=Y$![]() , where $Y^{d-1}$
, where $Y^{d-1}$![]() is the $(d-1)$
is the $(d-1)$![]() -skeleton of $Y$
-skeleton of $Y$![]() , and $Y_i$
, and $Y_i$![]() is obtained by attaching one $d$
is obtained by attaching one $d$![]() -cell to $Y_{i-1}$
-cell to $Y_{i-1}$![]() . By the inductive assumption, we have $\chi (f^{-1}(Y^{d-1}))=\chi (Y^{d-1})$
. By the inductive assumption, we have $\chi (f^{-1}(Y^{d-1}))=\chi (Y^{d-1})$![]() . Suppose we already proved $\chi (f^{-1}(Y_{i-1}))=\chi (Y_{i-1})$
. Suppose we already proved $\chi (f^{-1}(Y_{i-1}))=\chi (Y_{i-1})$![]() . Let $Y_i=Y_{i-1}\cup \sigma$
. Let $Y_i=Y_{i-1}\cup \sigma$![]() for a $d$
for a $d$![]() -cell $\sigma$
-cell $\sigma$![]() . Then $Y_{i-1}\cap \sigma$
. Then $Y_{i-1}\cap \sigma$![]() is a CW-complex of dimension $< d$
is a CW-complex of dimension $< d$![]() . Therefore, we have $\chi (f^{-1}(Y_{i-1}\cap \sigma ))=\chi (Y_{i-1}\cap \sigma )$
. Therefore, we have $\chi (f^{-1}(Y_{i-1}\cap \sigma ))=\chi (Y_{i-1}\cap \sigma )$![]() by the inductive assumption. Combined with $\chi (f^{-1}(\sigma ))=1=\chi (\sigma )$
by the inductive assumption. Combined with $\chi (f^{-1}(\sigma ))=1=\chi (\sigma )$![]() , we get
, we get

Inductively, this proves $\chi (F)=\chi (f^{-1}(Y_k))=\chi (Y_k)=\chi (Y)$![]() .
.
The converse of lemma 2.1 is true up to homotopy equivalence.
Lemma 2.2 Suppose $Y$![]() is a finite connected regular CW-complex. Suppose $F\ne \emptyset$
is a finite connected regular CW-complex. Suppose $F\ne \emptyset$![]() and $f\colon F\to Y$
and $f\colon F\to Y$![]() is a map, such that $\chi (F)=\chi (Y)$
is a map, such that $\chi (F)=\chi (Y)$![]() mod $n$
mod $n$![]() . Then there is a homotopy equivalence $\phi \colon F\simeq \widehat {F}$
. Then there is a homotopy equivalence $\phi \colon F\simeq \widehat {F}$![]() and a map $\widehat {f}\colon \widehat {F}\to Y$
and a map $\widehat {f}\colon \widehat {F}\to Y$![]() , such that $\widehat {f}\phi \simeq f$
, such that $\widehat {f}\phi \simeq f$![]() , and $\chi (\widehat {f}^{-1}(\sigma ))=1$
, and $\chi (\widehat {f}^{-1}(\sigma ))=1$![]() mod $n$
mod $n$![]() for every cell $\sigma$
for every cell $\sigma$![]() of $Y$
of $Y$![]() .
.
Proof. We call a cell top cell if it is not in the boundary of any other cell. Fix $c\in F$![]() and a top cell $\beta$
and a top cell $\beta$![]() containing $f(c)$
containing $f(c)$![]() . We regard $\beta$
. We regard $\beta$![]() as the ‘base cell’ of $Y$
as the ‘base cell’ of $Y$![]() . For each top cell $\sigma$
. For each top cell $\sigma$![]() different from $\beta$
different from $\beta$![]() , there is a continuous path $\gamma \colon [-1,1]\to Y$
, there is a continuous path $\gamma \colon [-1,1]\to Y$![]() , such that $\gamma (-1)=f(c)$
, such that $\gamma (-1)=f(c)$![]() , $\gamma (-1,0)\cap \sigma =\emptyset$
, $\gamma (-1,0)\cap \sigma =\emptyset$![]() and $\gamma (0,1]\subset \mathring {\sigma }=\sigma -\partial \sigma$
and $\gamma (0,1]\subset \mathring {\sigma }=\sigma -\partial \sigma$![]() . This implies that $\gamma (0)\in \partial \sigma$
. This implies that $\gamma (0)\in \partial \sigma$![]() , and $f(c)$
, and $f(c)$![]() is the only other possible point on the path lying inside $\partial \sigma$
is the only other possible point on the path lying inside $\partial \sigma$![]() .
.

For any two spaces $A$![]() and $B$
and $B$![]() , we glue cones $cA$
, we glue cones $cA$![]() and $cB$
and $cB$![]() to $F$
to $F$![]() by identifying the cone points with $c$
by identifying the cone points with $c$![]() . The new space $F'=F\cup _c(cA\cup cB)$
. The new space $F'=F\cup _c(cA\cup cB)$![]() is homotopy equivalent to $F$
is homotopy equivalent to $F$![]() . We further extend $f$
. We further extend $f$![]() to $f'\colon F'\to Y$
to $f'\colon F'\to Y$![]() by mapping the cones to the path $\gamma$
by mapping the cones to the path $\gamma$![]() in $Y$
in $Y$![]() . The map is ‘straightforward’ on $cA$
. The map is ‘straightforward’ on $cA$![]() and is ‘twisted’ on $cB$
and is ‘twisted’ on $cB$![]() , as illustrated by the picture. Let $\chi (A)=a$
, as illustrated by the picture. Let $\chi (A)=a$![]() and $\chi (B)=b$
and $\chi (B)=b$![]() . Then we have
. Then we have

It is therefore possible to choose $a$![]() and $b$
and $b$![]() , such that $\chi (f'^{-1}(\sigma ))=\chi (\sigma )=1$
, such that $\chi (f'^{-1}(\sigma ))=\chi (\sigma )=1$![]() and $\chi (f'^{-1}(\partial \sigma ))=\chi (\partial \sigma )=1-(-1)^{\dim \sigma }$
and $\chi (f'^{-1}(\partial \sigma ))=\chi (\partial \sigma )=1-(-1)^{\dim \sigma }$![]() . By $\chi (F)=\chi (Y)$
. By $\chi (F)=\chi (Y)$![]() mod $n$
mod $n$![]() , this implies that $\chi (f'^{-1}(Y-\mathring {\sigma }))=\chi (Y-\mathring {\sigma })$
, this implies that $\chi (f'^{-1}(Y-\mathring {\sigma }))=\chi (Y-\mathring {\sigma })$![]() mod $n$
mod $n$![]() .
.
The basic construction above reduces the problem to the restriction map $f'|\colon f'^{-1}(Y-\mathring {\sigma })\to Y-\mathring {\sigma }$![]() , which still satisfies the Euler characteristic condition in the lemma. This accommodates an inductive argument. We make the stronger inductive assumption that $f'^{-1}(Y-\mathring {\sigma })$
, which still satisfies the Euler characteristic condition in the lemma. This accommodates an inductive argument. We make the stronger inductive assumption that $f'^{-1}(Y-\mathring {\sigma })$![]() can be extended to $F''$
can be extended to $F''$![]() by glueing cones (identifying cone points with $c$
by glueing cones (identifying cone points with $c$![]() ), and $f'|\colon f'^{-1}(Y-\mathring {\sigma })\to Y-\mathring {\sigma }$
), and $f'|\colon f'^{-1}(Y-\mathring {\sigma })\to Y-\mathring {\sigma }$![]() can be extended to $f''\colon F''\to Y-\mathring {\sigma }$
can be extended to $f''\colon F''\to Y-\mathring {\sigma }$![]() , such that $\chi (f''^{-1}(\tau ))=1$
, such that $\chi (f''^{-1}(\tau ))=1$![]() mod $n$
mod $n$![]() for every cell $\tau$
for every cell $\tau$![]() of $Y-\mathring {\sigma }$
of $Y-\mathring {\sigma }$![]() . Then $\widehat {F}=F''\cup _c(cA\cup cB)$
. Then $\widehat {F}=F''\cup _c(cA\cup cB)$![]() is obtained by glueing cones to $F$
is obtained by glueing cones to $F$![]() (identifying cone points with $c$
(identifying cone points with $c$![]() ). Therefore, $\widehat {F}$
). Therefore, $\widehat {F}$![]() is homotopy equivalent to $F$
is homotopy equivalent to $F$![]() , and $\widehat {f}=f'\cup f''\colon \widehat {F}\to Y$
, and $\widehat {f}=f'\cup f''\colon \widehat {F}\to Y$![]() is homotopy equivalent to $f$
is homotopy equivalent to $f$![]() . Moreover, we still have $\chi (\widehat {f}^{-1}(\tau ))=\chi (f''^{-1}(\tau ))=1$
. Moreover, we still have $\chi (\widehat {f}^{-1}(\tau ))=\chi (f''^{-1}(\tau ))=1$![]() for every cell $\tau$
for every cell $\tau$![]() of $Y-\mathring {\sigma }$
of $Y-\mathring {\sigma }$![]() . By applying lemma 2.1 to the restriction $\widehat {f}|\colon \widehat {f}^{-1}(\partial \sigma )\to \partial \sigma$
. By applying lemma 2.1 to the restriction $\widehat {f}|\colon \widehat {f}^{-1}(\partial \sigma )\to \partial \sigma$![]() , where cells of $\partial \sigma$
, where cells of $\partial \sigma$![]() are cells of $Y-\mathring {\sigma }$
are cells of $Y-\mathring {\sigma }$![]() , we get
, we get
On the other hand, we have
Therefore, $\chi (\widehat {f}^{-1}(\sigma ))=\chi (f'^{-1}(\sigma ))=1$![]() .
.
There are two problems with the induction argument. The first is that $Y-\mathring {\sigma }$![]() may not be connected. The second is that there may be only one top cell $\beta$
may not be connected. The second is that there may be only one top cell $\beta$![]() .
.
The case $Y-\mathring {\sigma }$![]() not connected happens only when $\sigma$
not connected happens only when $\sigma$![]() is a $1$
is a $1$![]() -cell, with only one end $v_0$
-cell, with only one end $v_0$![]() attached to $Y-\mathring {\sigma }$
attached to $Y-\mathring {\sigma }$![]() , and other end $v_1$
, and other end $v_1$![]() being ‘free’. In addition to glueing $cA$
being ‘free’. In addition to glueing $cA$![]() and $cB$
and $cB$![]() , we may further glue a cone $cC$
, we may further glue a cone $cC$![]() , with the map from $cC$
, with the map from $cC$![]() to $Y$
to $Y$![]() extending all the way to $v_1$
extending all the way to $v_1$![]() . Then we have
. Then we have

It is then possible to choose $a,b,c$![]() , such that $\chi (f'^{-1}(\sigma ))=\chi (f'^{-1}(v_0))=\chi (f'^{-1}(v_1))=1$
, such that $\chi (f'^{-1}(\sigma ))=\chi (f'^{-1}(v_0))=\chi (f'^{-1}(v_1))=1$![]() . The rest of the inductive argument is the same.
. The rest of the inductive argument is the same.

Finally, we consider the case $Y$![]() has only one top cell $\beta$
has only one top cell $\beta$![]() . In this case, the assumption already says $\chi (f^{-1}(\beta ))=1$
. In this case, the assumption already says $\chi (f^{-1}(\beta ))=1$![]() , and additional cone construction over $\beta$
, and additional cone construction over $\beta$![]() does not change this fact. What we need to do is to improve $\chi (f^{-1}(\sigma ))$
does not change this fact. What we need to do is to improve $\chi (f^{-1}(\sigma ))$![]() to $1$
to $1$![]() for cells $\sigma$
for cells $\sigma$![]() in $\partial \beta$
in $\partial \beta$![]() . The problem is then reduced to the restriction map $f|\colon f^{-1}(\partial \beta )\to \partial \beta$
. The problem is then reduced to the restriction map $f|\colon f^{-1}(\partial \beta )\to \partial \beta$![]() . The induction may continue over $\partial \beta$
. The induction may continue over $\partial \beta$![]() .
.
3. Non-empty fixed point set
We prove theorem 1.7, for the case $F_C=f^{-1}(C)$![]() is not empty for every connected component $C$
is not empty for every connected component $C$![]() of $Y^G$
of $Y^G$![]() . The next section deals with the case some $F_C=\emptyset$
. The next section deals with the case some $F_C=\emptyset$![]() .
.
To construct the pseudo-equivalence extension, we will first homotopically modify $f\colon F\to Y^G$![]() to a better map described in lemma 2.2. Then we construct the extension by inducting on skeleta of $Y^G$
to a better map described in lemma 2.2. Then we construct the extension by inducting on skeleta of $Y^G$![]() . The following justifies the homotopy modification of $f$
. The following justifies the homotopy modification of $f$![]() .
.
Lemma 3.1 Suppose $Y$![]() is a finite $G$
is a finite $G$![]() -CW-complex, and $F$
-CW-complex, and $F$![]() is a finite CW-complex with trivial $G$
is a finite CW-complex with trivial $G$![]() -action. If a $G$
-action. If a $G$![]() -map $f\colon F\to Y$
-map $f\colon F\to Y$![]() has pseudo-equivalence extension, and we change $f,F,Y$
has pseudo-equivalence extension, and we change $f,F,Y$![]() by equivariant homotopy, then the new map also has pseudo-equivalence extension.
by equivariant homotopy, then the new map also has pseudo-equivalence extension.
Proof. Suppose $g\colon X\to Y$![]() is a pseudo-equivalence extension of $f\colon F\to Y$
is a pseudo-equivalence extension of $f\colon F\to Y$![]() . We homotopically change $f,F,Y$
. We homotopically change $f,F,Y$![]() one by one, and argue about the pseudo-equivalence extension of the new map.
one by one, and argue about the pseudo-equivalence extension of the new map.
First, suppose $f$![]() is $G$
is $G$![]() -homotopic to $f'\colon F\to Y$
-homotopic to $f'\colon F\to Y$![]() . By the equivariant version of the homotopy extension property, the $G$
. By the equivariant version of the homotopy extension property, the $G$![]() -homotopy extends to a $G$
-homotopy extends to a $G$![]() -homotopy from $g\colon X\to Y$
-homotopy from $g\colon X\to Y$![]() to another $G$
to another $G$![]() -map $g'\colon X\to Y$
-map $g'\colon X\to Y$![]() . Then the $G$
. Then the $G$![]() -map $g'$
-map $g'$![]() extends $f'$
extends $f'$![]() , and $g'$
, and $g'$![]() is still a pseudo-equivalence.
is still a pseudo-equivalence.
Second, suppose $\phi \colon F\to F'$![]() is a $G$
is a $G$![]() -homotopy equivalence. Then there is a $G$
-homotopy equivalence. Then there is a $G$![]() -map $f'\colon F'\to Y$
-map $f'\colon F'\to Y$![]() , such that $f\colon F\to Y$
, such that $f\colon F\to Y$![]() is $G$
is $G$![]() -homotopic to $f'\circ \phi \colon F\to F'\to Y$
-homotopic to $f'\circ \phi \colon F\to F'\to Y$![]() . By the argument above, $f'\circ \phi$
. By the argument above, $f'\circ \phi$![]() has pseudo-equivalence extension $g'\colon X\to Y$
has pseudo-equivalence extension $g'\colon X\to Y$![]() . Then $X'=X\cup _{\phi } F'$
. Then $X'=X\cup _{\phi } F'$![]() (glueing $F\subset X$
(glueing $F\subset X$![]() to $F'$
to $F'$![]() by $\phi$
by $\phi$![]() ) is a $G$
) is a $G$![]() -CW-complex with $F'$
-CW-complex with $F'$![]() as the fixed set, and the $G$
as the fixed set, and the $G$![]() -map $g'\cup f'\colon X'\to Y$
-map $g'\cup f'\colon X'\to Y$![]() is a pseudo-equivalence extension of $f'$
is a pseudo-equivalence extension of $f'$![]() .
.
Finally, suppose $\psi \colon Y\to Y'$![]() is a $G$
is a $G$![]() -homotopy equivalence. Then $\psi \circ f\colon F\to Y'$
-homotopy equivalence. Then $\psi \circ f\colon F\to Y'$![]() is extended to a pseudo-equivalence $\psi \circ g\colon X\to Y'$
is extended to a pseudo-equivalence $\psi \circ g\colon X\to Y'$![]() .
.
For the inductive construction (on skeleta of $Y^G$![]() ) of pseudo-equivalence extension, we use the following result.
) of pseudo-equivalence extension, we use the following result.
Lemma 3.2 Suppose $G$![]() is a group of not prime power order, $K$
is a group of not prime power order, $K$![]() is a finite $G$
is a finite $G$![]() -CW-complex and $F=K^G$
-CW-complex and $F=K^G$![]() .
.
1. If $\chi (F)=1$
 mod $m(G)$
mod $m(G)$ , then $K$
, then $K$ can be extended to a finite $G$
can be extended to a finite $G$ -CW-complex $X$
-CW-complex $X$ , such that $F=X^G$
, such that $F=X^G$ , $X$
, $X$ is $(\dim X-1)$
is $(\dim X-1)$ -connected and $H_{\dim X}(X;{\mathbb {Z}})$
-connected and $H_{\dim X}(X;{\mathbb {Z}})$ is a projective ${\mathbb {Z}}G$
is a projective ${\mathbb {Z}}G$ -module.
-module.2. If $\chi (F)=1$
 mod $n(G)$
mod $n(G)$ , then $K$
, then $K$ can be extended to a finite contractible $G$
can be extended to a finite contractible $G$ -CW-complex $X$
-CW-complex $X$ , such that $F=X^G$
, such that $F=X^G$ .
.
Proof. The first statement is [Reference Oliver10, theorem 2], and Oliver called the $G$![]() -CW-complex $X$
-CW-complex $X$![]() in the statement a $G$
in the statement a $G$![]() -resolution. The second statement is essentially the corollary to [Reference Oliver10, theorem 3]. More precisely, we may use [Reference Oliver11, theorem 2], which is even applicable to compact Lie group actions: Let ${\mathcal {F}}$
-resolution. The second statement is essentially the corollary to [Reference Oliver10, theorem 3]. More precisely, we may use [Reference Oliver11, theorem 2], which is even applicable to compact Lie group actions: Let ${\mathcal {F}}$![]() be a family of subgroups of $G$
be a family of subgroups of $G$![]() as defined by tom Dieck, meaning closed under subgroup and conjugation. If ${\mathcal {F}}$
as defined by tom Dieck, meaning closed under subgroup and conjugation. If ${\mathcal {F}}$![]() contains all the prime toral subgroups, $X$
contains all the prime toral subgroups, $X$![]() and $Z$
and $Z$![]() are finite $G$
are finite $G$![]() -CW-complexes, $Z$
-CW-complexes, $Z$![]() is contractible and $\chi (X^H/NH)=\chi (Z^H/NH)$
is contractible and $\chi (X^H/NH)=\chi (Z^H/NH)$![]() for all $H\not \in {\mathcal {F}}$
for all $H\not \in {\mathcal {F}}$![]() , then $X$
, then $X$![]() can be extended to a finite contractible $G$
can be extended to a finite contractible $G$![]() -CW-complex $Y$
-CW-complex $Y$![]() , such that the isotropy subgroups of $Y-X$
, such that the isotropy subgroups of $Y-X$![]() are in ${\mathcal {F}}$
are in ${\mathcal {F}}$![]() .
.
Let
Then the proof of [Reference Oliver11, lemma 14] shows that $\chi (X^H/NH)=\chi (Z^H/NH)$![]() for all $H\not \in {\mathcal {F}}$
for all $H\not \in {\mathcal {F}}$![]() if and only if $\delta _H(X)=\delta _H(Z)$
if and only if $\delta _H(X)=\delta _H(Z)$![]() for all $H\not \in {\mathcal {F}}$
for all $H\not \in {\mathcal {F}}$![]() .
.
By [Reference Oliver11, theorem 3], the assumption $\chi (F)=1$![]() mod $n(G)$
mod $n(G)$![]() implies $F=Z^G$
implies $F=Z^G$![]() for a finite contractible $G$
for a finite contractible $G$![]() -CW-complex $Z$
-CW-complex $Z$![]() . Let ${\mathcal {F}}$
. Let ${\mathcal {F}}$![]() be the family of all the prime toral subgroups of $G$
be the family of all the prime toral subgroups of $G$![]() . By adding $G/H\times D^j$
. By adding $G/H\times D^j$![]() to $K$
to $K$![]() , for $H\not \in {\mathcal {F}}\cup \{G\}$
, for $H\not \in {\mathcal {F}}\cup \{G\}$![]() , it is easy to get a finite $G$
, it is easy to get a finite $G$![]() -CW-complex $L$
-CW-complex $L$![]() , such that $\delta _H(L)=\delta _H(Z)$
, such that $\delta _H(L)=\delta _H(Z)$![]() for all $H\not \in {\mathcal {F}}\cup \{G\}$
for all $H\not \in {\mathcal {F}}\cup \{G\}$![]() . Since $H\ne G$
. Since $H\ne G$![]() in the construction of $L$
in the construction of $L$![]() , we have $L^G=K^G=F=Z^G$
, we have $L^G=K^G=F=Z^G$![]() . Therefore, we also have $\delta _G(L)=\chi (L^G)=\chi (Z^G)=\delta _G(Z)$
. Therefore, we also have $\delta _G(L)=\chi (L^G)=\chi (Z^G)=\delta _G(Z)$![]() , and we get $\delta _H(L)=\delta _H(Z)$
, and we get $\delta _H(L)=\delta _H(Z)$![]() for all $H\not \in {\mathcal {F}}$
for all $H\not \in {\mathcal {F}}$![]() . This implies $\chi (L^H/NH)=\chi (Z^H/NH)$
. This implies $\chi (L^H/NH)=\chi (Z^H/NH)$![]() for all $H\not \in {\mathcal {F}}$
for all $H\not \in {\mathcal {F}}$![]() . Then by the interpretation of [Reference Oliver11, theorem 2] above, $L$
. Then by the interpretation of [Reference Oliver11, theorem 2] above, $L$![]() extends to a finite contractible $G$
extends to a finite contractible $G$![]() -CW-complex $X$
-CW-complex $X$![]() , such that the isotropy subgroups of $X-L$
, such that the isotropy subgroups of $X-L$![]() are in ${\mathcal {F}}$
are in ${\mathcal {F}}$![]() . Since $G$
. Since $G$![]() is not an isotropy subgroup of $X-L$
is not an isotropy subgroup of $X-L$![]() , we have $X^G=L^G=F$
, we have $X^G=L^G=F$![]() .
.
Proof Proof of theorem 1.7 in case all $F_C\ne \emptyset$
The $G$![]() -CW-complex $Y$
-CW-complex $Y$![]() is $G$
is $G$![]() -homotopy equivalent to a regular $G$
-homotopy equivalent to a regular $G$![]() -CW-complex. If all $F_C$
-CW-complex. If all $F_C$![]() are not empty, then we apply lemma 2.2 to homotopically modify all $F_C\to C$
are not empty, then we apply lemma 2.2 to homotopically modify all $F_C\to C$![]() , such that $\chi (f^{-1}(\sigma ))=1$
, such that $\chi (f^{-1}(\sigma ))=1$![]() mod $n(G)$
mod $n(G)$![]() for every cell $\sigma$
for every cell $\sigma$![]() of $Y^G$
of $Y^G$![]() . By lemma 3.1, it is sufficient to construct a pseudo-equivalence extension under the additional assumption.
. By lemma 3.1, it is sufficient to construct a pseudo-equivalence extension under the additional assumption.
Denote $Z=Y^G$![]() , which has trivial $G$
, which has trivial $G$![]() -action. We first extend $f\colon F\to Z$
-action. We first extend $f\colon F\to Z$![]() to a pseudo-equivalence $h\colon W\to Z$
to a pseudo-equivalence $h\colon W\to Z$![]() by inducting on the skeleta of $Z$
by inducting on the skeleta of $Z$![]() .
.
We assume $F^{k-1}=f^{-1}(Z^{k-1})$![]() is already extended to a $G$
is already extended to a $G$![]() -CW-complex $W^{k-1}$
-CW-complex $W^{k-1}$![]() with $(W^{k-1})^G=F^{k-1}$
with $(W^{k-1})^G=F^{k-1}$![]() . Moreover, we assume that $f|_{F^{k-1}}$
. Moreover, we assume that $f|_{F^{k-1}}$![]() is extended to a $G$
is extended to a $G$![]() -map $h_{k-1}\colon W^{k-1}\to Z^{k-1}$
-map $h_{k-1}\colon W^{k-1}\to Z^{k-1}$![]() , such that $h_{k-1}^{-1}(\sigma )$
, such that $h_{k-1}^{-1}(\sigma )$![]() is contractible for every cell $\sigma$
is contractible for every cell $\sigma$![]() of $Z^{k-1}$
of $Z^{k-1}$![]() . The inductive assumption holds for $k=0$
. The inductive assumption holds for $k=0$![]() , because $Z^{-1}=F^{-1}=\emptyset$
, because $Z^{-1}=F^{-1}=\emptyset$![]() .
.
Let $\sigma$![]() be a $k$
be a $k$![]() -cell of $Z$
-cell of $Z$![]() . Then $\chi (f^{-1}(\sigma ))=1$
. Then $\chi (f^{-1}(\sigma ))=1$![]() mod $n(G)$
mod $n(G)$![]() by our assumption. Taking $f^{-1}(\sigma )$
by our assumption. Taking $f^{-1}(\sigma )$![]() and $f^{-1}(\sigma )\cup h_{k-1}^{-1}(\partial \sigma )$
and $f^{-1}(\sigma )\cup h_{k-1}^{-1}(\partial \sigma )$![]() as $F$
as $F$![]() and $K$
and $K$![]() in the second part of lemma 3.2, we may extend $f^{-1}(\sigma )\cup h_{k-1}^{-1}(\partial \sigma )$
in the second part of lemma 3.2, we may extend $f^{-1}(\sigma )\cup h_{k-1}^{-1}(\partial \sigma )$![]() to a finite contractible $G$
to a finite contractible $G$![]() -CW-complex $W_{\sigma }$
-CW-complex $W_{\sigma }$![]() , such that $W_{\sigma }^G=f^{-1}(\sigma )$
, such that $W_{\sigma }^G=f^{-1}(\sigma )$![]() . Since $\sigma$
. Since $\sigma$![]() is contractible and has trivial $G$
is contractible and has trivial $G$![]() -action, we may further arrange to extend $f|_{\sigma }\cup h_{k-1}|_{\partial \sigma }$
-action, we may further arrange to extend $f|_{\sigma }\cup h_{k-1}|_{\partial \sigma }$![]() to a $G$
to a $G$![]() -map $h_{\sigma }\colon W_{\sigma }\to \sigma$
-map $h_{\sigma }\colon W_{\sigma }\to \sigma$![]() , such that $h_{\sigma }^{-1}(\partial \sigma )= h_{k-1}^{-1}(\partial \sigma )$
, such that $h_{\sigma }^{-1}(\partial \sigma )= h_{k-1}^{-1}(\partial \sigma )$![]() .
.
Let $W^k=W^{k-1}\cup (\cup _{\dim \sigma =k}W_{\sigma })$![]() , where the union identifies $h_{k-1}^{-1}(\partial \sigma )\subset W_{\sigma }$
, where the union identifies $h_{k-1}^{-1}(\partial \sigma )\subset W_{\sigma }$![]() with the same subset in $W^{k-1}$
with the same subset in $W^{k-1}$![]() . Then we have $G$
. Then we have $G$![]() -map $h_k=h_{k-1}\cup (\cup _{\dim \sigma =k}h_{\sigma })\colon W^k\to Z^k$
-map $h_k=h_{k-1}\cup (\cup _{\dim \sigma =k}h_{\sigma })\colon W^k\to Z^k$![]() , such that $(W^k)^G=F^{k-1}\cup (\cup _{\dim \sigma =k}f^{-1}(\sigma ))=F_k$
, such that $(W^k)^G=F^{k-1}\cup (\cup _{\dim \sigma =k}f^{-1}(\sigma ))=F_k$![]() . Moreover, we have $h_k^{-1}(\sigma )=W_{\sigma }$
. Moreover, we have $h_k^{-1}(\sigma )=W_{\sigma }$![]() if $\dim \sigma =k$
if $\dim \sigma =k$![]() , and $h_k^{-1}(\sigma )=h_{k-1}^{-1}(\sigma )$
, and $h_k^{-1}(\sigma )=h_{k-1}^{-1}(\sigma )$![]() if $\dim \sigma < k$
if $\dim \sigma < k$![]() . Therefore $h_k^{-1}(\sigma )$
. Therefore $h_k^{-1}(\sigma )$![]() is contractible for every cell $\sigma$
is contractible for every cell $\sigma$![]() of $Z^k$
of $Z^k$![]() .
.
When $k=\dim Z$![]() , we get $h=h_{\dim Z}\colon W=W^{\dim Z}\to Z$
, we get $h=h_{\dim Z}\colon W=W^{\dim Z}\to Z$![]() , such that $W^G=F$
, such that $W^G=F$![]() , and $h^{-1}(\sigma )$
, and $h^{-1}(\sigma )$![]() is contractible for every cell $\sigma$
is contractible for every cell $\sigma$![]() of $Z$
of $Z$![]() . This implies that $h\colon W\to Z=Y^G$
. This implies that $h\colon W\to Z=Y^G$![]() is a homotopy equivalence.
is a homotopy equivalence.
Next, we further extend $h\colon W\to Z=Y^G\subset Y$![]() to a pseudo-equivalence ${g\colon X\to Y}$
to a pseudo-equivalence ${g\colon X\to Y}$![]() .
.
The equivariant neighbourhood $\text {nd}(Z)$![]() of $Z$
of $Z$![]() in $Y$
in $Y$![]() is the mapping cylinder of a $G$
is the mapping cylinder of a $G$![]() -map $\lambda \colon E\to Z$
-map $\lambda \colon E\to Z$![]() . We try to factor $\lambda$
. We try to factor $\lambda$![]() through a $G$
through a $G$![]() -map $\widetilde {\lambda }\colon E\to W$
-map $\widetilde {\lambda }\colon E\to W$![]() . Then $\lambda =h\circ \widetilde {\lambda }$
. Then $\lambda =h\circ \widetilde {\lambda }$![]() , and we have a $G$
, and we have a $G$![]() -map from the mapping cylinder of $\widetilde {\lambda }\colon E\to W$
-map from the mapping cylinder of $\widetilde {\lambda }\colon E\to W$![]() to the mapping cylinder of $\lambda \colon E\to Z$
to the mapping cylinder of $\lambda \colon E\to Z$![]() . The $G$
. The $G$![]() -map extends to a $G$
-map extends to a $G$![]() -map $g=id\cup h\colon X=(Y-\text {nd}(Z))\cup _{\widetilde {\lambda }}W\to Y=(Y-\text {nd}(Z))\cup _{\lambda }Z$
-map $g=id\cup h\colon X=(Y-\text {nd}(Z))\cup _{\widetilde {\lambda }}W\to Y=(Y-\text {nd}(Z))\cup _{\lambda }Z$![]() . We have $X^G=W^G=F$
. We have $X^G=W^G=F$![]() , and $g$
, and $g$![]() extends $f$
extends $f$![]() . Moreover, since $h$
. Moreover, since $h$![]() is a pseudo-equivalence, $g$
is a pseudo-equivalence, $g$![]() is also a pseudo-equivalence.
is also a pseudo-equivalence.
It remains to construct the lifting $\widetilde {\lambda }$![]() . Since $G$
. Since $G$![]() fixes no points on $E$
fixes no points on $E$![]() , we can construct the lifting if $h\colon W\to Z$
, we can construct the lifting if $h\colon W\to Z$![]() is highly connected for the fixed sets of proper subgroups of $G$
is highly connected for the fixed sets of proper subgroups of $G$![]() acting on $W$
acting on $W$![]() . Recall that we actually constructed $h\colon W\to Z$
. Recall that we actually constructed $h\colon W\to Z$![]() in such a way that, for every cell $\sigma$
in such a way that, for every cell $\sigma$![]() in the (regular) CW-complex $Z$
in the (regular) CW-complex $Z$![]() , $h^{-1}(\sigma )$
, $h^{-1}(\sigma )$![]() is contractible. Let $S$
is contractible. Let $S$![]() be the disjoint union of all the $G$
be the disjoint union of all the $G$![]() -orbits appearing in $E$
-orbits appearing in $E$![]() . Then $S$
. Then $S$![]() is a compact set, such that all the isotropies on $E$
is a compact set, such that all the isotropies on $E$![]() appear in $S$
appear in $S$![]() . Then we may take the cell-wise join of $h\colon W\to Z$
. Then we may take the cell-wise join of $h\colon W\to Z$![]() with $S\times Z\to Z$
with $S\times Z\to Z$![]() several times to get $h'\colon W'\to Z$
several times to get $h'\colon W'\to Z$![]() . This means $h'^{-1}(\sigma )=h^{-1}(\sigma )*S*\cdots *S$
. This means $h'^{-1}(\sigma )=h^{-1}(\sigma )*S*\cdots *S$![]() . Since $h^{-1}(\sigma )$
. Since $h^{-1}(\sigma )$![]() is contractible, $h'^{-1}(\sigma )$
is contractible, $h'^{-1}(\sigma )$![]() is still contractible. Since $G$
is still contractible. Since $G$![]() fixes no points of $S$
fixes no points of $S$![]() , we get $W'^G=W^G=F$
, we get $W'^G=W^G=F$![]() . Therefore, $h'$
. Therefore, $h'$![]() is still a pseudo-equivalence extension of $f$
is still a pseudo-equivalence extension of $f$![]() . On the other hand, the fixed sets of proper subgroups of $G$
. On the other hand, the fixed sets of proper subgroups of $G$![]() acting on $h'^{-1}(\sigma )$
acting on $h'^{-1}(\sigma )$![]() become more and more highly connected as we repeat the join construction more and more times. Therefore, we may construct the lifting $\widetilde {\lambda }$
become more and more highly connected as we repeat the join construction more and more times. Therefore, we may construct the lifting $\widetilde {\lambda }$![]() by using $h'$
by using $h'$![]() instead of $h$
instead of $h$![]() .
.
For the $G$![]() -ANR case, we only need to modify the proof in the very last cell. We may use Quinn's ‘wrinkling’ trick from [Reference Quinn15, § 2] to remove the $\widetilde {K}_0$
-ANR case, we only need to modify the proof in the very last cell. We may use Quinn's ‘wrinkling’ trick from [Reference Quinn15, § 2] to remove the $\widetilde {K}_0$![]() -obstruction arising in the first part of lemma 3.2, or more systematically, use his exact sequence in [Reference Quinn16] for the topological Whitehead groups and Wall finiteness groups where the relevant $K$
-obstruction arising in the first part of lemma 3.2, or more systematically, use his exact sequence in [Reference Quinn16] for the topological Whitehead groups and Wall finiteness groups where the relevant $K$![]() -groups are quotiented by the image of the assembly map.
-groups are quotiented by the image of the assembly map.
4. Empty fixed point
We still need to prove theorem 1.7 for the case some $F_C=\emptyset$![]() . In this case, $\chi (F_C)=\chi (C)$
. In this case, $\chi (F_C)=\chi (C)$![]() mod $n(G)$
mod $n(G)$![]() means $\chi (C)=0$
means $\chi (C)=0$![]() mod $n(G)$
mod $n(G)$![]() . A typical example is that $C$
. A typical example is that $C$![]() is the circle $S^1$
is the circle $S^1$![]() , and our proof starts with this special case. In fact, we first concentrate on the case $Y=Y^G=S^1$
, and our proof starts with this special case. In fact, we first concentrate on the case $Y=Y^G=S^1$![]() .
.
Lemma 4.1 Suppose $G$![]() is a group of not prime power order. Then there is a pseudo-equivalence $X\to S^1$
is a group of not prime power order. Then there is a pseudo-equivalence $X\to S^1$![]() , such that $X$
, such that $X$![]() is a finite $G$
is a finite $G$![]() -CW-complex without fixed points, and $G$
-CW-complex without fixed points, and $G$![]() fixes $S^1$
fixes $S^1$![]() .
.
The idea is to find a finite and simply connected $G$![]() -CW-complex $Z$
-CW-complex $Z$![]() without fixed points, and a $G$
without fixed points, and a $G$![]() -map $h\colon Z\to Z$
-map $h\colon Z\to Z$![]() inducing zero homomorphism on the reduced homology. Then the mapping torus $X$
inducing zero homomorphism on the reduced homology. Then the mapping torus $X$![]() of $h$
of $h$![]() together with the natural map to $S^1$
together with the natural map to $S^1$![]() gives what we want. We may take $Z=S(V)$
gives what we want. We may take $Z=S(V)$![]() and take $h$
and take $h$![]() to be the self map of $S(V)$
to be the self map of $S(V)$![]() in the following result.
in the following result.
Lemma 4.2 Suppose $G$![]() is a group of not prime power order, and $V$
is a group of not prime power order, and $V$![]() is a linear $G$
is a linear $G$![]() -representation. If $V^G=0$
-representation. If $V^G=0$![]() and all Sylow subgroups of $G$
and all Sylow subgroups of $G$![]() are isotropy groups of $V$
are isotropy groups of $V$![]() , then there is a degree $0$
, then there is a degree $0$![]() $G$
$G$![]() -map from the unit sphere $S(V)$
-map from the unit sphere $S(V)$![]() to itself.
to itself.
Proof. Let $P$![]() be a Sylow subgroup and let $NP$
be a Sylow subgroup and let $NP$![]() be its normalizer in $G$
be its normalizer in $G$![]() . Since $P$
. Since $P$![]() is an isotropy subgroup, the fixed subspace $V^P$
is an isotropy subgroup, the fixed subspace $V^P$![]() is not a zero subspace. Let $D$
is not a zero subspace. Let $D$![]() be a small equivariant disk neighbourhood of a point $x\in S(V^P)$
be a small equivariant disk neighbourhood of a point $x\in S(V^P)$![]() . Then $D$
. Then $D$![]() is an $NP$
is an $NP$![]() -representation. Moreover, since $V$
-representation. Moreover, since $V$![]() is a linear representation, the $NP$
is a linear representation, the $NP$![]() -representation is independent of the size of $D$
-representation is independent of the size of $D$![]() . This means that the radial extension gives an $NP$
. This means that the radial extension gives an $NP$![]() -equivariant homeomorphism $D/\partial D\cong S(V)$
-equivariant homeomorphism $D/\partial D\cong S(V)$![]() sending $*=\partial D/\partial D$
sending $*=\partial D/\partial D$![]() to $x$
to $x$![]() . Then we may construct an $NP$
. Then we may construct an $NP$![]() -map
-map
The first map collapses $\partial D$![]() to $x$
to $x$![]() , and the second map uses the $NP$
, and the second map uses the $NP$![]() -equivariant homeomorphism $D/\partial D\cong S(V)$
-equivariant homeomorphism $D/\partial D\cong S(V)$![]() . The map can be extended to a $G$
. The map can be extended to a $G$![]() -map
-map
If we fix an orientation of $S(V)$![]() , then $D$
, then $D$![]() inherits the orientation, and the homeomorphism $D/\partial D\cong S(V)$
inherits the orientation, and the homeomorphism $D/\partial D\cong S(V)$![]() has degree $\pm 1$
has degree $\pm 1$![]() . By composing with the $-1$
. By composing with the $-1$![]() map along a $1$
map along a $1$![]() -dimensional subspace of $V^P$
-dimensional subspace of $V^P$![]() , we may change the sign of the degree of the homeomorphism. Therefore, we may arrange to have the degree of $h_x$
, we may change the sign of the degree of the homeomorphism. Therefore, we may arrange to have the degree of $h_x$![]() to be $1+|G/NP|$
to be $1+|G/NP|$![]() or to be $1-|G/NP|$
or to be $1-|G/NP|$![]() . If we apply the construction at several points $x\in S(V^P)$
. If we apply the construction at several points $x\in S(V^P)$![]() with disjoint orbits $Gx$
with disjoint orbits $Gx$![]() , then we get a $G$
, then we get a $G$![]() -map $S(V)\to S(V)$
-map $S(V)\to S(V)$![]() of degree $1+a|G/NP|$
of degree $1+a|G/NP|$![]() for any integer $a$
for any integer $a$![]() . If we apply the construction to the Sylow subgroups $P_1,P_2,\dots,P_n$
. If we apply the construction to the Sylow subgroups $P_1,P_2,\dots,P_n$![]() for all the distinct prime factors of $|G|$
for all the distinct prime factors of $|G|$![]() , then we get a $G$
, then we get a $G$![]() -map $S(V)\to S(V)$
-map $S(V)\to S(V)$![]() of degree $1+\sum a_i|G/NP_i|$
of degree $1+\sum a_i|G/NP_i|$![]() , where $a_1,a_2,\dots,a_n$
, where $a_1,a_2,\dots,a_n$![]() can be any prescribed integers. Since $|G/NP_1|,|G/NP_2|,\dots,|G/NP_n|$
can be any prescribed integers. Since $|G/NP_1|,|G/NP_2|,\dots,|G/NP_n|$![]() are coprime, we get degree $0$
are coprime, we get degree $0$![]() by suitable choice of the integers $a_i$
by suitable choice of the integers $a_i$![]() .
.
Remark 4.3 We may further make $S(V)$![]() highly connected for the fixed sets of proper subgroups. Specifically, the kernel of the augmentation $\epsilon (\sum _{g\in G}a_gg)=\sum a_g\colon {\mathbb {R}}G\to {\mathbb {R}}$
highly connected for the fixed sets of proper subgroups. Specifically, the kernel of the augmentation $\epsilon (\sum _{g\in G}a_gg)=\sum a_g\colon {\mathbb {R}}G\to {\mathbb {R}}$![]() is a representation satisfying the condition of the lemma. The direct sum of several copies of this kernel also satisfies the condition of the lemma. By taking the direct sum of sufficiently many copies, the fixed sets of $S(V)$
is a representation satisfying the condition of the lemma. The direct sum of several copies of this kernel also satisfies the condition of the lemma. By taking the direct sum of sufficiently many copies, the fixed sets of $S(V)$![]() for proper subgroups are highly connected.
for proper subgroups are highly connected.
Remark 4.4 Lemma 4.1 is valid for non-prime toral compact Lie groups. Moreover, the remark above on the high connectivity is also valid.
Suppose a compact Lie group $G$![]() is not prime toral. If the identity component $G_0$
is not prime toral. If the identity component $G_0$![]() is not abelian (i.e., not torus), then by [Reference Oliver11, theorem 5], there is a finite contractible $G$
is not abelian (i.e., not torus), then by [Reference Oliver11, theorem 5], there is a finite contractible $G$![]() -CW-complex $Z$
-CW-complex $Z$![]() without fixed points. In fact, $Z$
without fixed points. In fact, $Z$![]() can be a disk with smooth $G$
can be a disk with smooth $G$![]() -action. Then $X=Z\times S^1\to S^1$
-action. Then $X=Z\times S^1\to S^1$![]() is a pseudo-equivalence, and $X^G=\emptyset$
is a pseudo-equivalence, and $X^G=\emptyset$![]() .
.
If $G_0$![]() is abelian, then the order of $G/G_0$
is abelian, then the order of $G/G_0$![]() is not prime power. We may apply lemma 4.2 to $G/G_0$
is not prime power. We may apply lemma 4.2 to $G/G_0$![]() , and then take the mapping cylinder to construct $X$
, and then take the mapping cylinder to construct $X$![]() . We obtain a $G/G_0$
. We obtain a $G/G_0$![]() -pseudo-equivalence $X\to S^1$
-pseudo-equivalence $X\to S^1$![]() , and $X$
, and $X$![]() has no $G/G_0$
has no $G/G_0$![]() -fixed points. This induces a $G$
-fixed points. This induces a $G$![]() -pseudo-equivalence $X\to S^1$
-pseudo-equivalence $X\to S^1$![]() , and $X$
, and $X$![]() still has no $G$
still has no $G$![]() -fixed points.
-fixed points.
Alternatively, we may use Bartsch's study of the existence of Borsuk–Ulam theorems [Reference Bartsch1] to find degree $0$![]() $G$
$G$![]() -map from a fixed point free representation sphere to itself. The equivalence of properties ($c$
-map from a fixed point free representation sphere to itself. The equivalence of properties ($c$![]() ) and ($d$
) and ($d$![]() ) of his theorem 1 gives such a map for finite groups of non-prime power order. The equivalence of properties ($c$
) of his theorem 1 gives such a map for finite groups of non-prime power order. The equivalence of properties ($c$![]() ) and ($d'$
) and ($d'$![]() ) of his theorem 2 gives such a map for non-prime toral compact Lie groups. The map on the representation sphere has degree $0$
) of his theorem 2 gives such a map for non-prime toral compact Lie groups. The map on the representation sphere has degree $0$![]() because it takes the whole sphere into a proper sub-sphere.
because it takes the whole sphere into a proper sub-sphere.
Proof Proof of theorem 1.7 in case some $F_C=\emptyset$
Assume $F_C=\emptyset$![]() for some $C$
for some $C$![]() . Then the condition $\chi (F_C)=\chi (C)$
. Then the condition $\chi (F_C)=\chi (C)$![]() mod $n(G)$
mod $n(G)$![]() means $\chi (C)=0=\chi (S^1)$
means $\chi (C)=0=\chi (S^1)$![]() mod $n(G)$
mod $n(G)$![]() .
.
If $F_C=\emptyset$![]() , then we introduce $F'_C=S^1\to C$
, then we introduce $F'_C=S^1\to C$![]() , where the map can be any one. If $F_C\ne \emptyset$
, where the map can be any one. If $F_C\ne \emptyset$![]() , then we let $F'_C=F_C$
, then we let $F'_C=F_C$![]() , and let the map $F'_C\to C$
, and let the map $F'_C\to C$![]() be $F_C\to C$
be $F_C\to C$![]() . Then $f\colon F\to Y^G$
. Then $f\colon F\to Y^G$![]() extends to $f'\colon F'=\cup F'_C\to Y^G$
extends to $f'\colon F'=\cup F'_C\to Y^G$![]() . The modification $f'$
. The modification $f'$![]() satisfies the Euler characteristic condition in the theorem, and all $F'_C$
satisfies the Euler characteristic condition in the theorem, and all $F'_C$![]() are not empty. Since the theorem is already proved for the case all $F_C\ne \emptyset$
are not empty. Since the theorem is already proved for the case all $F_C\ne \emptyset$![]() , $f'$
, $f'$![]() has a pseudo-equivalence extension $X'\to Y$
has a pseudo-equivalence extension $X'\to Y$![]() , with $X'^G=F'$
, with $X'^G=F'$![]() .
.
It remains to homotopically replace the extra circles added to $F$![]() by something that have no fixed points. The equivariant neighbourhood $\text {nd}(S^1)$
by something that have no fixed points. The equivariant neighbourhood $\text {nd}(S^1)$![]() of one such circle in $X'$
of one such circle in $X'$![]() is the mapping cylinder of a $G$
is the mapping cylinder of a $G$![]() -map $\lambda \colon E\to S^1$
-map $\lambda \colon E\to S^1$![]() . By lemma 4.1 and the remarks after the proof of lemma 4.2, there is a highly connected (for the fixed sets of proper subgroups) pseudo-equivalence $\mu \colon W\to S^1$
. By lemma 4.1 and the remarks after the proof of lemma 4.2, there is a highly connected (for the fixed sets of proper subgroups) pseudo-equivalence $\mu \colon W\to S^1$![]() , such that $W$
, such that $W$![]() has no fixed point. By the high connectivity, $\lambda$
has no fixed point. By the high connectivity, $\lambda$![]() can be lifted to a $G$
can be lifted to a $G$![]() -map $\widetilde {\lambda }\colon E\to W$
-map $\widetilde {\lambda }\colon E\to W$![]() . Then we have $\lambda =\mu \circ \widetilde {\lambda }$
. Then we have $\lambda =\mu \circ \widetilde {\lambda }$![]() . Let $X=(X'-\text {nd}(S^1))\cup _{\widetilde {\lambda }}W$
. Let $X=(X'-\text {nd}(S^1))\cup _{\widetilde {\lambda }}W$![]() be obtained by glueing the boundary $E$
be obtained by glueing the boundary $E$![]() of $\text {nd}(S^1)$
of $\text {nd}(S^1)$![]() to $W$
to $W$![]() , and this is done for all $F'_C=S^1\subset X'$
, and this is done for all $F'_C=S^1\subset X'$![]() that were used to replace empty $F_C$
that were used to replace empty $F_C$![]() . Then $\lambda =\mu \circ \widetilde {\lambda }$
. Then $\lambda =\mu \circ \widetilde {\lambda }$![]() and the pseudo-equivalence $\mu$
and the pseudo-equivalence $\mu$![]() induce a pseudo-equivalence $X\to X'=(X'-\text {nd}(S^1))\cup _{\lambda }S^1$
induce a pseudo-equivalence $X\to X'=(X'-\text {nd}(S^1))\cup _{\lambda }S^1$![]() . The composition $X\to X'\to Y$
. The composition $X\to X'\to Y$![]() is then a pseudo-equivalence extension of $f$
is then a pseudo-equivalence extension of $f$![]() with $X^G=F$
with $X^G=F$![]() .
.
We end the section by using lemma 4.1 to prove theorem 1.1.
Proof of theorem 1.1 By lemma 4.1, there is a $G$![]() -CW-complex $X$
-CW-complex $X$![]() without fixed point, and a pseudo-equivalence $f\colon X\to S^1$
without fixed point, and a pseudo-equivalence $f\colon X\to S^1$![]() , where $G$
, where $G$![]() fixes $S^1$
fixes $S^1$![]() . By thickening, we may assume $X$
. By thickening, we may assume $X$![]() is a manifold with boundary. Let $C$
is a manifold with boundary. Let $C$![]() be the mapping cylinder of $f$
be the mapping cylinder of $f$![]() . Then the inclusion $X\to C$
. Then the inclusion $X\to C$![]() is a pseudo-equivalence. We can now do a Davis construction [Reference Davis5, Reference Davis and Hausmann6] equivariantly on $X$
is a pseudo-equivalence. We can now do a Davis construction [Reference Davis5, Reference Davis and Hausmann6] equivariantly on $X$![]() (by triangulating the boundary) and mapping to the Davis construction on $C$
(by triangulating the boundary) and mapping to the Davis construction on $C$![]() (with respect to the boundary of $X$
(with respect to the boundary of $X$![]() ). This produces a $G$
). This produces a $G$![]() -action on a closed aspherical manifold $M$
-action on a closed aspherical manifold $M$![]() , with a pseudo-equivalence to the same construction on $C$
, with a pseudo-equivalence to the same construction on $C$![]() . Since $C$
. Since $C$![]() has a fixed point, the $G$
has a fixed point, the $G$![]() -action on $\pi =\pi _1(C)=\pi _1(X)$
-action on $\pi =\pi _1(C)=\pi _1(X)$![]() lifts to $\text {Aut}(\pi )$
lifts to $\text {Aut}(\pi )$![]() . On the other hand, the $G$
. On the other hand, the $G$![]() -action on $M$
-action on $M$![]() has no fixed point, because the original action on $X$
has no fixed point, because the original action on $X$![]() did not.
did not.
It is an interesting problem whether the action constructed in the proof can exist on classical aspherical manifolds, e.g., hyperbolic manifolds. For odd order cyclic group (or the order is a power of $2$![]() ), [Reference Weinberger19] shows the answer is negative.
), [Reference Weinberger19] shows the answer is negative.
5. Obstruction group
We prove theorem 1.6.
For a finite $G$![]() -CW-complex $Y$
-CW-complex $Y$![]() , let $N(Y)\subset {\mathbb {Z}}^{\pi _0Y^G}$
, let $N(Y)\subset {\mathbb {Z}}^{\pi _0Y^G}$![]() be the collection of
be the collection of
for all pseudo-equivalences $g\colon X\to Y$![]() . We prove $N(Y)$
. We prove $N(Y)$![]() is a group, by showing that it is closed under negative and addition operations.
is a group, by showing that it is closed under negative and addition operations.
For a pseudo-equivalence $g\colon X\to Y$![]() , we construct its negative to be the double mapping cylinder of $g$
, we construct its negative to be the double mapping cylinder of $g$![]()
Then $\overline {g}$![]() is still a pseudo-equivalence, with $\overline {F}_C=C\cup F_C\times [0,1]\cup C$
is still a pseudo-equivalence, with $\overline {F}_C=C\cup F_C\times [0,1]\cup C$![]() , and $\chi (\overline {F}_C)-\chi (C)=-(\chi (F_C)-\chi (C))$
, and $\chi (\overline {F}_C)-\chi (C)=-(\chi (F_C)-\chi (C))$![]() . Therefore, $\nu \in N(Y)$
. Therefore, $\nu \in N(Y)$![]() implies $-\nu \in N(Y)$
implies $-\nu \in N(Y)$![]() .
.
The negative construction has the following properties:
1. $\overline {X}$
 contains a copy of $Y$
contains a copy of $Y$ , and the non-equivariant homotopy equivalence can be a homotopy retraction of $\overline {X}$
, and the non-equivariant homotopy equivalence can be a homotopy retraction of $\overline {X}$ to $Y$
to $Y$ .
.2. $\overline {F}_C$
 is connected. Therefore, the connected components of the fixed sets of $\overline {X}$
is connected. Therefore, the connected components of the fixed sets of $\overline {X}$ and $Y$
and $Y$ are in one-to-one correspondence.
are in one-to-one correspondence.
We call a pseudo-equivalence with the two properties retracting equivalence. Since the double negative satisfies $\nu (\overline {\overline {g}})=\nu (g)$![]() , every element in $N(Y)$
, every element in $N(Y)$![]() is represented by a retracting equivalence.
is represented by a retracting equivalence.
For two retracting equivalences $g_1\colon X_1\to Y$![]() and $g_2\colon X_2\to Y$
and $g_2\colon X_2\to Y$![]() , the addition $g_1\cup g_2\colon X_1\cup _Y X_2\to Y$
, the addition $g_1\cup g_2\colon X_1\cup _Y X_2\to Y$![]() is still a retracting equivalence. It is also easy to see that $\nu (g_1\cup g_2)=\nu (g_1)+\nu (g_2)$
is still a retracting equivalence. It is also easy to see that $\nu (g_1\cup g_2)=\nu (g_1)+\nu (g_2)$![]() . Therefore, $\nu _1,\nu _2\in N(Y)$
. Therefore, $\nu _1,\nu _2\in N(Y)$![]() implies $\nu _1+\nu _2\in N(Y)$
implies $\nu _1+\nu _2\in N(Y)$![]() .
.
This completes the proof that $N(Y)$![]() is an abelian subgroup. Next, we prove that $N(Y)$
is an abelian subgroup. Next, we prove that $N(Y)$![]() is indeed the obstruction to pseudo-equivalence extension.
is indeed the obstruction to pseudo-equivalence extension.
By the definition of $N(Y)$![]() , if $f\colon F\to Y$
, if $f\colon F\to Y$![]() extends to a pseudo-equivalence $g\colon X\to Y$
extends to a pseudo-equivalence $g\colon X\to Y$![]() , such that $X^G=F$
, such that $X^G=F$![]() , then $(\chi (F_C)-\chi (C))_{C\in \pi _0Y^G}=\nu (g)\in N(Y)$
, then $(\chi (F_C)-\chi (C))_{C\in \pi _0Y^G}=\nu (g)\in N(Y)$![]() .
.
Conversely, suppose $f\colon F\to Y$![]() satisfies $(\chi (F_C)-\chi (C))_{C\in \pi _0Y^G}\in N(Y)$
satisfies $(\chi (F_C)-\chi (C))_{C\in \pi _0Y^G}\in N(Y)$![]() . Then $(\chi (F_C)-\chi (C))_{C\in \pi _0Y^G}=\nu (g')$
. Then $(\chi (F_C)-\chi (C))_{C\in \pi _0Y^G}=\nu (g')$![]() for a pseudo-equivalence $g'\colon X'\to Y$
for a pseudo-equivalence $g'\colon X'\to Y$![]() . This means $\chi (F_C)=\chi (F'_C)$
. This means $\chi (F_C)=\chi (F'_C)$![]() , where $F'_C=g'^{-1}(C)\cap X'^G$
, where $F'_C=g'^{-1}(C)\cap X'^G$![]() .
.
As remarked earlier, we may further assume that $g'$![]() is a retracting equivalence. Then we may regard $f$
is a retracting equivalence. Then we may regard $f$![]() as mapped into $Y\subset X'$
as mapped into $Y\subset X'$![]() . This means $f$
. This means $f$![]() is the composition ($i\colon Y\to X'$
is the composition ($i\colon Y\to X'$![]() is the inclusion)
is the inclusion)
Since $Y\subset X'$![]() , and connected components of the fixed sets of $X'$
, and connected components of the fixed sets of $X'$![]() and $Y$
and $Y$![]() are in one-to-one correspondence, we have
are in one-to-one correspondence, we have
and
By theorem 1.7, this implies that $i\circ f$![]() has pseudo-equivalence extension $h\colon X\to X'$
has pseudo-equivalence extension $h\colon X\to X'$![]() . Then $g'\circ h\colon X\to Y$
. Then $g'\circ h\colon X\to Y$![]() is a pseudo-equivalence extension of $f$
is a pseudo-equivalence extension of $f$![]() . This completes the proof of theorem 1.6.
. This completes the proof of theorem 1.6.
6. The role of the fundamental group
In this section, we develop an equivariant Euler–Wall characteristic of a finite $G$![]() -CW-complex; it lies in $K_0(R[\Gamma ])$
-CW-complex; it lies in $K_0(R[\Gamma ])$![]() , for rings $R$
, for rings $R$![]() in which the orders of isotropy groups are invertible. We apply this to get further restrictions on the Euler characteristics of components of fixed sets under pseudo-equivalences.
in which the orders of isotropy groups are invertible. We apply this to get further restrictions on the Euler characteristics of components of fixed sets under pseudo-equivalences.
We first elaborate on the lifted $G$![]() -actions to the universal cover that we use to define the weakly $G$
-actions to the universal cover that we use to define the weakly $G$![]() -connected property in the introduction.
-connected property in the introduction.
Let $p\colon \widetilde {Y}\to Y$![]() be the universal cover, with free action on $\widetilde {Y}$
be the universal cover, with free action on $\widetilde {Y}$![]() by the fundamental group $\pi =\pi _1(Y)$
by the fundamental group $\pi =\pi _1(Y)$![]() . A $G$
. A $G$![]() -action on $Y$
-action on $Y$![]() lifts to self homeomorphisms of $\widetilde {Y}$
lifts to self homeomorphisms of $\widetilde {Y}$![]() . All the liftings form a group $\Gamma$
. All the liftings form a group $\Gamma$![]() fitting into an exact sequence
fitting into an exact sequence
Strictly speaking, we only get an exact sequence with $G/G_0$![]() in place of $G$
in place of $G$![]() , where $G_0$
, where $G_0$![]() consists of all the elements of $G$
consists of all the elements of $G$![]() that act trivially on $Y$
that act trivially on $Y$![]() . Then we replace $\Gamma$
. Then we replace $\Gamma$![]() by the pullback of $\Gamma \to G/G_0\leftarrow G$
by the pullback of $\Gamma \to G/G_0\leftarrow G$![]() and still get (6.1) with $G$
and still get (6.1) with $G$![]() instead of $G/G_0$
instead of $G/G_0$![]() .
.
Let $\widetilde {y}\in \widetilde {Y}$![]() , $y=p(\widetilde {y})$
, $y=p(\widetilde {y})$![]() . The induced homomorphism $\Gamma _{\widetilde {y}}\to G_y$
. The induced homomorphism $\Gamma _{\widetilde {y}}\to G_y$![]() of isotropy groups is an isomorphism. If $y\in Y^G$
of isotropy groups is an isomorphism. If $y\in Y^G$![]() , then we get a splitting $G=G_y\cong \Gamma _{\widetilde {y}}\subset \Gamma$
, then we get a splitting $G=G_y\cong \Gamma _{\widetilde {y}}\subset \Gamma$![]() of (6.1). If $\widetilde {y}$
of (6.1). If $\widetilde {y}$![]() and $\widetilde {y}'$
and $\widetilde {y}'$![]() are in the same connected component $\widehat {C}$
are in the same connected component $\widehat {C}$![]() of $p^{-1}(Y^G)$
of $p^{-1}(Y^G)$![]() , then $\Gamma _{\widetilde {y}}=\Gamma _{\widetilde {y}'}$
, then $\Gamma _{\widetilde {y}}=\Gamma _{\widetilde {y}'}$![]() . Therefore, we may denote $\Gamma _{\widetilde {y}}=\Gamma _{\widehat {C}}$
. Therefore, we may denote $\Gamma _{\widetilde {y}}=\Gamma _{\widehat {C}}$![]() , and the splitting $G\cong \Gamma _{\widehat {C}}\subset \Gamma$
, and the splitting $G\cong \Gamma _{\widehat {C}}\subset \Gamma$![]() depends only on $\widehat {C}$
depends only on $\widehat {C}$![]() .
.
The connected component $\widehat {C}$![]() covers a connected component $C$
covers a connected component $C$![]() of $Y^G$
of $Y^G$![]() . The other connected components of $p^{-1}(C)$
. The other connected components of $p^{-1}(C)$![]() are $a\widehat {C}$
are $a\widehat {C}$![]() , $a\in \pi$
, $a\in \pi$![]() . Therefore, a connected component $C$
. Therefore, a connected component $C$![]() of $Y^G$
of $Y^G$![]() gives a $\pi$
gives a $\pi$![]() -conjugacy class of splittings of (6.1),
-conjugacy class of splittings of (6.1),
Example 6.1 The complex conjugation action of $G={\mathbb {Z}}_2$![]() on circle $Y=S^1$
on circle $Y=S^1$![]() has fixed point components $C_1=\{1\}$
has fixed point components $C_1=\{1\}$![]() and $C_{-1}=\{-1\}$
and $C_{-1}=\{-1\}$![]() . The universal cover is $p(t)=e^{it}\colon \widetilde {Y}={\mathbb {R}}\to Y$
. The universal cover is $p(t)=e^{it}\colon \widetilde {Y}={\mathbb {R}}\to Y$![]() . The group $\Gamma$
. The group $\Gamma$![]() consists of $\sigma _n(t)=t+2n\pi$
consists of $\sigma _n(t)=t+2n\pi$![]() (liftings of the identity, which form $\pi _1(Y)$
(liftings of the identity, which form $\pi _1(Y)$![]() ) and $\rho _n(t)=-t+2n\pi$
) and $\rho _n(t)=-t+2n\pi$![]() (liftings of the conjugation). We have
(liftings of the conjugation). We have

We have two conjugate families of splittings
A splitting of (6.1) corresponds to a semi-direct product decomposition $\Gamma =\pi \rtimes G$![]() . The $\pi$
. The $\pi$![]() -conjugacy classes of splittings form the cohomology set $H^1(G;\pi )$
-conjugacy classes of splittings form the cohomology set $H^1(G;\pi )$![]() (not necessarily a group because $\pi$
(not necessarily a group because $\pi$![]() may not be commutative).
may not be commutative).
A $G$![]() -map $g\colon X\to Y$
-map $g\colon X\to Y$![]() has a pullback $\widetilde {g}\colon \widetilde {X}\to \widetilde {Y}$
has a pullback $\widetilde {g}\colon \widetilde {X}\to \widetilde {Y}$![]() along the universal cover $p\colon \widetilde {Y}\to Y$
along the universal cover $p\colon \widetilde {Y}\to Y$![]() . The map $\widetilde {g}$
. The map $\widetilde {g}$![]() is a $\Gamma$
is a $\Gamma$![]() -map, and induces a map of ${\mathbb {Z}}[\Gamma ]$
-map, and induces a map of ${\mathbb {Z}}[\Gamma ]$![]() -chain complexes $\widetilde {g}_*\colon C(\widetilde {X})\to C(\widetilde {Y})$
-chain complexes $\widetilde {g}_*\colon C(\widetilde {X})\to C(\widetilde {Y})$![]() . If $g$
. If $g$![]() is a pseudo-equivalence, then $\widetilde {g}_*$
is a pseudo-equivalence, then $\widetilde {g}_*$![]() has a ${\mathbb {Z}}[\pi ]$
has a ${\mathbb {Z}}[\pi ]$![]() -chain homotopy inverse $\varphi$
-chain homotopy inverse $\varphi$![]() .
.
Let $R$![]() be a ring, say the rational numbers ${\mathbb {Q}}$
be a ring, say the rational numbers ${\mathbb {Q}}$![]() , such that $|G|$
, such that $|G|$![]() is invertible in $R$
is invertible in $R$![]() . Then we may use one splitting $\Gamma =\pi \rtimes G$
. Then we may use one splitting $\Gamma =\pi \rtimes G$![]() to get a $R[\Gamma ]$
to get a $R[\Gamma ]$![]() -chain map $\frac {1}{|G|}\sum _{u\in G}u\varphi \colon C(\widetilde {Y})\to C(\widetilde {X})$
-chain map $\frac {1}{|G|}\sum _{u\in G}u\varphi \colon C(\widetilde {Y})\to C(\widetilde {X})$![]() . This is a $R[\Gamma ]$
. This is a $R[\Gamma ]$![]() -chain homotopy inverse of
-chain homotopy inverse of
In particular, $\widetilde {g}_*\otimes R$![]() is a $R[\Gamma ]$
is a $R[\Gamma ]$![]() -chain homotopy equivalence.
-chain homotopy equivalence.
Since $|G|$![]() is invertible in $R$
is invertible in $R$![]() , and the isotropy groups of the $\Gamma$
, and the isotropy groups of the $\Gamma$![]() -action are isomorphic to subgroups of $G$
-action are isomorphic to subgroups of $G$![]() , we know $C(\widetilde {X})\otimes R$
, we know $C(\widetilde {X})\otimes R$![]() and $C(\widetilde {Y})\otimes R$
and $C(\widetilde {Y})\otimes R$![]() consist of finitely generated projective $R[\Gamma ]$
consist of finitely generated projective $R[\Gamma ]$![]() -modules. Then the $R[\Gamma ]$
-modules. Then the $R[\Gamma ]$![]() -chain complexes give the Euler characteristic elements $\chi _{\Gamma }(\widetilde {X})$
-chain complexes give the Euler characteristic elements $\chi _{\Gamma }(\widetilde {X})$![]() and $\chi _{\Gamma }(\widetilde {Y})$
and $\chi _{\Gamma }(\widetilde {Y})$![]() in $K_0(R[\Gamma ])$
in $K_0(R[\Gamma ])$![]() . The $R[\Gamma ]$
. The $R[\Gamma ]$![]() -chain homotopy equivalence $\widetilde {g}_*\otimes R$
-chain homotopy equivalence $\widetilde {g}_*\otimes R$![]() implies $\chi _{\Gamma }(\widetilde {X})=\chi _{\Gamma }(\widetilde {Y})$
implies $\chi _{\Gamma }(\widetilde {X})=\chi _{\Gamma }(\widetilde {Y})$![]() .
.
The $G$![]() -cells $G\sigma$
-cells $G\sigma$![]() of $Y$
of $Y$![]() are in one-to-one correspondence with $\Gamma$
are in one-to-one correspondence with $\Gamma$![]() -cells $\Gamma \widetilde {\sigma }$
-cells $\Gamma \widetilde {\sigma }$![]() of $\widetilde {Y}$
of $\widetilde {Y}$![]() , where $\widetilde {\sigma }$
, where $\widetilde {\sigma }$![]() is any cell of $\widetilde {Y}$
is any cell of $\widetilde {Y}$![]() over $\sigma$
over $\sigma$![]() . The Euler characteristic of $C(\widetilde {Y})\otimes R$
. The Euler characteristic of $C(\widetilde {Y})\otimes R$![]() is
is
Here $\Gamma \widetilde {\sigma }=\Gamma /\Gamma _{\widetilde {\sigma }}$![]() is a $\Gamma$
is a $\Gamma$![]() -orbit, and $R[\Gamma \widetilde {\sigma }]$
-orbit, and $R[\Gamma \widetilde {\sigma }]$![]() is a projective $R[\Gamma ]$
is a projective $R[\Gamma ]$![]() -module. For a finite subgroup $H$
-module. For a finite subgroup $H$![]() , the rank [Reference Bass2, Reference Hattori7, Reference Stallings18] of the projective $R[\Gamma ]$
, the rank [Reference Bass2, Reference Hattori7, Reference Stallings18] of the projective $R[\Gamma ]$![]() -module $R[\Gamma /H]$
-module $R[\Gamma /H]$![]() is ($(\gamma )$
is ($(\gamma )$![]() is the conjugacy class of $\gamma$
is the conjugacy class of $\gamma$![]() in $\Gamma$
in $\Gamma$![]() )
)
By $\chi _{\Gamma }(\widetilde {X})=\chi _{\Gamma }(\widetilde {Y})$![]() , we have $\text {rank}(\chi _{\Gamma }(\widetilde {X}))=\text {rank}(\chi _{\Gamma }(\widetilde {Y}))$
, we have $\text {rank}(\chi _{\Gamma }(\widetilde {X}))=\text {rank}(\chi _{\Gamma }(\widetilde {Y}))$![]() .
.
Theorem 6.2 Suppose $G$![]() is a cyclic group acting on a finite $G$
is a cyclic group acting on a finite $G$![]() -CW-complex $Y$
-CW-complex $Y$![]() . Suppose $\gamma \in \Gamma$
. Suppose $\gamma \in \Gamma$![]() is mapped to a generator of $G$
is mapped to a generator of $G$![]() , and $\langle \gamma \rangle$
, and $\langle \gamma \rangle$![]() is the cyclic subgroup generated by $\gamma$
is the cyclic subgroup generated by $\gamma$![]() . If $g\colon X\to Y$
. If $g\colon X\to Y$![]() is a rational pseudo-equivalence, then
is a rational pseudo-equivalence, then
The sum is over all components $C$![]() of $Y^G$
of $Y^G$![]() satisfying $\langle \gamma \rangle \in \Gamma _C$
satisfying $\langle \gamma \rangle \in \Gamma _C$![]() .
.
If $Y$![]() is weakly $G$
is weakly $G$![]() -connected, then there is at most one $C$
-connected, then there is at most one $C$![]() satisfying $\langle \gamma \rangle \in \Gamma _C$
satisfying $\langle \gamma \rangle \in \Gamma _C$![]() , and the proposition says $\chi (F_C)=\chi (C)$
, and the proposition says $\chi (F_C)=\chi (C)$![]() for each $C$
for each $C$![]() . In other words, the local Euler characteristic condition in theorem 1.7 is necessary and sufficient. This proves theorem 1.5 for the case $G$
. In other words, the local Euler characteristic condition in theorem 1.7 is necessary and sufficient. This proves theorem 1.5 for the case $G$![]() is cyclic, and we have $N(Y)=n(G){\mathbb {Z}}^{\pi _0Y^G}$
is cyclic, and we have $N(Y)=n(G){\mathbb {Z}}^{\pi _0Y^G}$![]() .
.
Proof. Since $\gamma \in \Gamma$![]() is mapped to a generator of $G$
is mapped to a generator of $G$![]() , by the formula for $\text {rank}({\mathbb {Q}}[\Gamma \widetilde {\sigma }])=\text {rank}({\mathbb {Q}}[\Gamma /\Gamma _{\widetilde {\sigma }}])$
, by the formula for $\text {rank}({\mathbb {Q}}[\Gamma \widetilde {\sigma }])=\text {rank}({\mathbb {Q}}[\Gamma /\Gamma _{\widetilde {\sigma }}])$![]() , the conjugacy class $(\gamma )$
, the conjugacy class $(\gamma )$![]() appears in $\text {rank}({\mathbb {Q}}[\Gamma \widetilde {\sigma }])$
appears in $\text {rank}({\mathbb {Q}}[\Gamma \widetilde {\sigma }])$![]() if and only if a conjugate of $\gamma$
if and only if a conjugate of $\gamma$![]() fixes $\widetilde {\sigma }$
fixes $\widetilde {\sigma }$![]() . Moreover, for such $\widetilde {\sigma }$
. Moreover, for such $\widetilde {\sigma }$![]() , we have
, we have

The elements $\gamma ^i$![]() are not $\Gamma$
are not $\Gamma$![]() -conjugate because they are mapped to non-conjugate elements of the cyclic group $G$
-conjugate because they are mapped to non-conjugate elements of the cyclic group $G$![]() . Therefore, the coefficient of $(\gamma )$
. Therefore, the coefficient of $(\gamma )$![]() in $\text {rank}({\mathbb {Q}}[\Gamma \widetilde {\sigma }])$
in $\text {rank}({\mathbb {Q}}[\Gamma \widetilde {\sigma }])$![]() is $\frac {1}{n}$
is $\frac {1}{n}$![]() .
.
The terms ${\mathbb {Q}}[\Gamma \widetilde {\sigma }]$![]() of $C(\widetilde {Y})\otimes {\mathbb {Q}}$
of $C(\widetilde {Y})\otimes {\mathbb {Q}}$![]() are in one-to-one correspondence with $G$
are in one-to-one correspondence with $G$![]() -cells $G\sigma$
-cells $G\sigma$![]() of $Y$
of $Y$![]() . If a conjugate of $\gamma$
. If a conjugate of $\gamma$![]() fixes $\widetilde {\sigma }$
fixes $\widetilde {\sigma }$![]() , by $\gamma$
, by $\gamma$![]() mapped to a generator of $G$
mapped to a generator of $G$![]() , we know $G$
, we know $G$![]() fixes $\sigma$
fixes $\sigma$![]() . Therefore, $\sigma$
. Therefore, $\sigma$![]() is in a connected component $C$
is in a connected component $C$![]() of $Y^G$
of $Y^G$![]() satisfying $\langle \gamma \rangle \in \Gamma _C$
satisfying $\langle \gamma \rangle \in \Gamma _C$![]() . Conversely, any such $\sigma$
. Conversely, any such $\sigma$![]() gives $\frac {1}{n}(\gamma )$
gives $\frac {1}{n}(\gamma )$![]() in the corresponding $\text {rank}({\mathbb {Q}}[\Gamma \widetilde {\sigma }])$
in the corresponding $\text {rank}({\mathbb {Q}}[\Gamma \widetilde {\sigma }])$![]() . Therefore, the coefficient of $(\gamma )$
. Therefore, the coefficient of $(\gamma )$![]() in
in
is

We have the same calculation for the pullback $\widetilde {X}$![]() , and find that the coefficient of $(\gamma )$
, and find that the coefficient of $(\gamma )$![]() in $\text {rank}(\chi _{\Gamma }(\widetilde {X}))$
in $\text {rank}(\chi _{\Gamma }(\widetilde {X}))$![]() is $\frac {1}{n}\sum _{\langle \gamma \rangle \in \Gamma _C}\chi (F_C)$
is $\frac {1}{n}\sum _{\langle \gamma \rangle \in \Gamma _C}\chi (F_C)$![]() . Then we conclude $\frac {1}{n}\sum _{\langle \gamma \rangle \in \Gamma _C}\chi (F_C)=\frac {1}{n}\sum _{\langle \gamma \rangle \in \Gamma _C}\chi (C)$
. Then we conclude $\frac {1}{n}\sum _{\langle \gamma \rangle \in \Gamma _C}\chi (F_C)=\frac {1}{n}\sum _{\langle \gamma \rangle \in \Gamma _C}\chi (C)$![]() .
.
Next, we apply the idea to $G$![]() satisfying $n(G)=0$
satisfying $n(G)=0$![]() . This means there is a normal subgroup $P$
. This means there is a normal subgroup $P$![]() , such that $|P|=p^l$
, such that $|P|=p^l$![]() for a prime $p$
for a prime $p$![]() , and $G/P$
, and $G/P$![]() is cyclic of order $n$
is cyclic of order $n$![]() . We may further assume that $p$
. We may further assume that $p$![]() and $n$
and $n$![]() are coprime. The liftings of $P$
are coprime. The liftings of $P$![]() -actions give an exact sequence
-actions give an exact sequence
Here $\Pi$![]() is the pre-image of $P$
is the pre-image of $P$![]() under $\Gamma \to G$
under $\Gamma \to G$![]() , and (6.2) is part of (6.1).
, and (6.2) is part of (6.1).
Each connected component $C$![]() of $Y^G$
of $Y^G$![]() is contained in a connected component $D$
is contained in a connected component $D$![]() of $Y^P$
of $Y^P$![]() . Then $p^{-1}(C)\subset p^{-1}(D)$
. Then $p^{-1}(C)\subset p^{-1}(D)$![]() , and each connected component $\widehat {C}$
, and each connected component $\widehat {C}$![]() of $p^{-1}(C)$
of $p^{-1}(C)$![]() is contained in a connected component $\widehat {D}$
is contained in a connected component $\widehat {D}$![]() of $p^{-1}(D)$
of $p^{-1}(D)$![]() . The pair $(\widehat {C},\widehat {D})$
. The pair $(\widehat {C},\widehat {D})$![]() gives a pair of compatible splittings $G\cong \Gamma _{\widehat {C}}\subset \Gamma$
gives a pair of compatible splittings $G\cong \Gamma _{\widehat {C}}\subset \Gamma$![]() and $P\cong \Gamma _{\widehat {D}}\subset \Pi$
and $P\cong \Gamma _{\widehat {D}}\subset \Pi$![]() of (6.1) and (6.2). All the pairs $(\widehat {C},\widehat {D})$
of (6.1) and (6.2). All the pairs $(\widehat {C},\widehat {D})$![]() are related by $\pi$
are related by $\pi$![]() -translations, and the corresponding pairs of splittings are $\pi$
-translations, and the corresponding pairs of splittings are $\pi$![]() -conjugate. Then we get a $\pi$
-conjugate. Then we get a $\pi$![]() -conjugacy class of compatible splittings (we fix one pair $(\widehat {C},\widehat {D})$
-conjugacy class of compatible splittings (we fix one pair $(\widehat {C},\widehat {D})$![]() in the second expression)
in the second expression)
Theorem 6.3 Suppose $P$![]() is a normal $p$
is a normal $p$![]() -subgroup of $G$
-subgroup of $G$![]() , and $G/P$
, and $G/P$![]() is a cyclic group of order prime to $p$
is a cyclic group of order prime to $p$![]() . Suppose $X,Y$
. Suppose $X,Y$![]() are finite $G$
are finite $G$![]() -CW-complexes, and a $G$
-CW-complexes, and a $G$![]() -map $g\colon X\to Y$
-map $g\colon X\to Y$![]() is a pseudo-equivalence. Then for connected components $C_0,D_0$
is a pseudo-equivalence. Then for connected components $C_0,D_0$![]() of $Y^G,Y^P$
of $Y^G,Y^P$![]() satisfying $C_0\subset D_0$
satisfying $C_0\subset D_0$![]() , we have
, we have
The sum is over all connected components $C$![]() of $Y^G$
of $Y^G$![]() satisfying $\Gamma _{CD_0}=\Gamma _{C_0D_0}$
satisfying $\Gamma _{CD_0}=\Gamma _{C_0D_0}$![]() .
.
The condition $\Gamma _{CD_0}=\Gamma _{C_0D_0}$![]() means the following: We fix one connected component $D$
means the following: We fix one connected component $D$![]() (denoted $D_0$
(denoted $D_0$![]() in the proposition) of $Y^P$
in the proposition) of $Y^P$![]() , and consider all the connected components $C$
, and consider all the connected components $C$![]() of $Y^G$
of $Y^G$![]() that are contained in $D$
that are contained in $D$![]() . Then we further distinguish these $C$
. Then we further distinguish these $C$![]() by the conjugation classes of the associated splittings. The sum of Euler characteristics is over such conjugation classes.
by the conjugation classes of the associated splittings. The sum of Euler characteristics is over such conjugation classes.
If all connected components $C$![]() inside $D$
inside $D$![]() have non-conjugate splittings, then the sum is over a single $C$
have non-conjugate splittings, then the sum is over a single $C$![]() , and we get $\chi (F_C)=\chi (C)$
, and we get $\chi (F_C)=\chi (C)$![]() for every $C$
for every $C$![]() inside $D$
inside $D$![]() . Furthermore, suppose $Y$
. Furthermore, suppose $Y$![]() has the property that, if connected components $C$
has the property that, if connected components $C$![]() and $C'$
and $C'$![]() of $Y^G$
of $Y^G$![]() give conjugate splittings, then $C$
give conjugate splittings, then $C$![]() and $C'$
and $C'$![]() belong to different connected components of $Y^P$
belong to different connected components of $Y^P$![]() . Of course, a weakly $G$
. Of course, a weakly $G$![]() -connected $Y$
-connected $Y$![]() has this property. Under this property, we get $\chi (F_C)=\chi (C)$
has this property. Under this property, we get $\chi (F_C)=\chi (C)$![]() for every connected component $C$
for every connected component $C$![]() of $Y^G$
of $Y^G$![]() . This proves theorem 1.5 for the case $n(G)=0$
. This proves theorem 1.5 for the case $n(G)=0$![]() .
.
Proof. The cyclic group $H=G/P$![]() acts on $Y^P$
acts on $Y^P$![]() , and the group $\widetilde {H}$
, and the group $\widetilde {H}$![]() of liftings of $H$
of liftings of $H$![]() -actions to $p^{-1}(Y^P)$
-actions to $p^{-1}(Y^P)$![]() fits into an exact sequence
fits into an exact sequence
By Smith theory [Reference Cappell, Weinberger and Yan4, Reference Smith17], we know $g^P\colon X^P\to Y^P$![]() is an ${\mathbb {F}}_p[\widetilde {H}]$
is an ${\mathbb {F}}_p[\widetilde {H}]$![]() -homology equivalence. This implies $g^P$
-homology equivalence. This implies $g^P$![]() is a ${\mathbb {Z}}_{p^k}[\widetilde {H}]$
is a ${\mathbb {Z}}_{p^k}[\widetilde {H}]$![]() -homology equivalence for all $k$
-homology equivalence for all $k$![]() .
.
The homology equivalence is a sum of homology equivalences on connected components [Reference Cappell, Weinberger and Yan4]. Let $C,D,\widehat {C},\widehat {D}$![]() be given as in the discussion before the proposition. Since $G$
be given as in the discussion before the proposition. Since $G$![]() has fixed set $C$
has fixed set $C$![]() in $D$
in $D$![]() , we know $H=G/P$
, we know $H=G/P$![]() acts on $D$
acts on $D$![]() . Then $\widehat {D}$
. Then $\widehat {D}$![]() covers $D$
covers $D$![]() , and the group $H_{\widehat {D}}$
, and the group $H_{\widehat {D}}$![]() of liftings of $H$
of liftings of $H$![]() -actions to $\widehat {D}$
-actions to $\widehat {D}$![]() fits into an exact sequence
fits into an exact sequence
Here $\pi _{\widehat {D}}$![]() is the subgroup of translations $a\in \pi$
is the subgroup of translations $a\in \pi$![]() satisfying $a\widehat {D}=\widehat {D}$
satisfying $a\widehat {D}=\widehat {D}$![]() , and (6.4) is part of (6.3). Let $\widehat {F}_D$
, and (6.4) is part of (6.3). Let $\widehat {F}_D$![]() be the pullback of $g^{-1}(D)\cap X^P\to D\leftarrow \widehat {D}$
be the pullback of $g^{-1}(D)\cap X^P\to D\leftarrow \widehat {D}$![]() , then the restriction of $g^P$
, then the restriction of $g^P$![]() induces a ${\mathbb {Z}}_{p^k}[H_{\widehat {D}}]$
induces a ${\mathbb {Z}}_{p^k}[H_{\widehat {D}}]$![]() -chain homology equivalence
-chain homology equivalence
We note that $\Gamma _{\widehat {C}}/\Gamma _{\widehat {D}}\cong H$![]() . In fact, by $\Gamma _{\widehat {C}}/\Gamma _{\widehat {D}}\subset H_{\widehat {D}}$
. In fact, by $\Gamma _{\widehat {C}}/\Gamma _{\widehat {D}}\subset H_{\widehat {D}}$![]() , we have a splitting of (6.4). For fixed $D,\widehat {D}$
, we have a splitting of (6.4). For fixed $D,\widehat {D}$![]() , the other choices of $\widehat {C}\subset \widehat {D}$
, the other choices of $\widehat {C}\subset \widehat {D}$![]() over the same $C$
over the same $C$![]() give $\pi _{\widehat {D}}$
give $\pi _{\widehat {D}}$![]() -conjugations of the splitting. These conjugations are in one-to-one correspondence with the conjugations of the pair $(\Gamma _{\widehat {C}},\Gamma _{\widehat {D}})$
-conjugations of the splitting. These conjugations are in one-to-one correspondence with the conjugations of the pair $(\Gamma _{\widehat {C}},\Gamma _{\widehat {D}})$![]() . Therefore, $\Gamma _{CD}$
. Therefore, $\Gamma _{CD}$![]() is also the $\pi _{\widehat {D}}$
is also the $\pi _{\widehat {D}}$![]() -conjugacy class of the splittings of (6.4).
-conjugacy class of the splittings of (6.4).
Let $\gamma \in \Gamma _{\widehat {C}}/\Gamma _{\widehat {D}}$![]() correspond to a generator of the cyclic group $H$
correspond to a generator of the cyclic group $H$![]() . Since $p$
. Since $p$![]() and $n$
and $n$![]() are coprime, the order $n=|H|=|\Gamma _{\widehat {C}}/\Gamma _{\widehat {D}}|$
are coprime, the order $n=|H|=|\Gamma _{\widehat {C}}/\Gamma _{\widehat {D}}|$![]() is invertible in the ring ${\mathbb {Z}}_{p^k}$
is invertible in the ring ${\mathbb {Z}}_{p^k}$![]() . Therefore, both chain complexes in (6.5) consist of projective ${\mathbb {Z}}_{p^k}[H_{\widehat {D}}]$
. Therefore, both chain complexes in (6.5) consist of projective ${\mathbb {Z}}_{p^k}[H_{\widehat {D}}]$![]() -modules, and the homology equivalence is a ${\mathbb {Z}}_{p^k}[H_{\widehat {D}}]$
-modules, and the homology equivalence is a ${\mathbb {Z}}_{p^k}[H_{\widehat {D}}]$![]() -chain homotopy equivalence. Then we may apply the same idea as in the proof of theorem 6.2, with ${\mathbb {Q}}$
-chain homotopy equivalence. Then we may apply the same idea as in the proof of theorem 6.2, with ${\mathbb {Q}}$![]() replaced by ${\mathbb {Z}}_{p^k}$
replaced by ${\mathbb {Z}}_{p^k}$![]() , and get a similar conclusion. We fix $C_0,D_0,\widehat {C}_0,\widehat {D}_0$
, and get a similar conclusion. We fix $C_0,D_0,\widehat {C}_0,\widehat {D}_0$![]() , and get the generator $\gamma \in \Gamma _{\widehat {C}_0}/\Gamma _{\widehat {D}_0}\subset H_{\widehat {D}_0}$
, and get the generator $\gamma \in \Gamma _{\widehat {C}_0}/\Gamma _{\widehat {D}_0}\subset H_{\widehat {D}_0}$![]() . Using the conjugacy class $\Gamma _{CD_0}$
. Using the conjugacy class $\Gamma _{CD_0}$![]() explained above, we conclude
explained above, we conclude
Here the equality is mod $p^k$![]() because it is an equality in ${\mathbb {Z}}_{p^k}$
because it is an equality in ${\mathbb {Z}}_{p^k}$![]() . We note that $\langle \gamma \rangle \in \Gamma _{CD_0}$
. We note that $\langle \gamma \rangle \in \Gamma _{CD_0}$![]() is the same as $\Gamma _{CD_0}=\Gamma _{C_0D_0}$
is the same as $\Gamma _{CD_0}=\Gamma _{C_0D_0}$![]() . Moreover, this equality holds mod $p^k$
. Moreover, this equality holds mod $p^k$![]() for all $k$
for all $k$![]() , which means the equality holds as integers.
, which means the equality holds as integers.
Acknowledgements
Sylvain Cappell’s research was partially supported by NYU Silver Professorship. Shmuel Weinberger’s research was partially supported by NSF grant DMS-2105451. Min Yan’s research was supported by Hong Kong RGC General Research Fund 16308018.