Hostname: page-component-669899f699-rg895 Total loading time: 0 Render date: 2025-04-25T05:21:15.315Z Has data issue: false hasContentIssue false
  • English
  • Français

Fixed point sets and the fundamental group I: semi-free actions on G-CW-complexes

Published online by Cambridge University Press:  03 August 2023

Sylvain Cappell Open the ORCID record for Sylvain Cappell [Opens in a new window] ,
Shmuel Weinberger  and
Min Yan Open the ORCID record for Min Yan [Opens in a new window]
Sylvain Cappell
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY, USA ([email protected])
Shmuel Weinberger
Affiliation:
University of Chicago, Chicago, IL, USA ([email protected])
Min Yan
Affiliation:
Hong Kong University of Science and Technology, Hong Kong, People's Republic of China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Smith theory says that the fixed point set of a semi-free action of a group 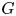$G$ on a contractible space is 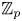${\mathbb {Z}}_p$-acyclic for any prime factor 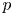$p$ of the order of 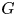$G$. Jones proved the converse of Smith theory for the case 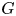$G$ is a cyclic group acting semi-freely on contractible, finite CW-complexes. We extend the theory to semi-free group actions on finite CW-complexes of given homotopy types, in various settings. In particular, the converse of Smith theory holds if and only if a certain 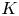$K$-theoretical obstruction vanishes. We also give some examples that show the geometrical effects of different types of 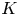$K$-theoretical obstructions.

Keywords

group actionsalgebraic K-theorySmith theory
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 6 , December 2024 , pp. 1639 - 1660
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Assadi, A. H., Finite Group Actions on Simply-connected Manifolds and CW complexes. Memoirs AMS, Vol.35, no. 257 (AMS, 1982).Google Scholar
Assadi, A. H. and Vogel, P.. Actions of finite groups on compact manifolds. Topology 26 (1987), 239–263.Google Scholar
Bartels, A. C.. On the domain of the assembly map in the algebraic $K$-theory. Alg. Geom. Topology 3 (2003), 1037–1050.Google Scholar
Bass, H.. Algebraic K-Theory (W. A. Benjamin, New York and Amsterdam, 1968).Google Scholar
Bass, H., Heller, A. and Swan, R.. The Whitehead group of a polynomial extension. Inst. Hautes Études Sci. Publ. Math. 22 (1964), 61–79.CrossRefGoogle Scholar
Bass, H. and Murthy, M. P.. Grothendieck groups and Picard groups of abelian group rings. Ann. Math. 86 (1967), 16–73.Google Scholar
Cappell, S. and Shaneson, J.. Nonlinear similarity. Ann. Math. 113 (1981), 315–355.CrossRefGoogle Scholar
Cappell, S., Weinberger, S. and Yan, M., Fixed point sets and the fundamental group II: Euler characteristics. preprint, 2021.Google Scholar
Carter, D.. Lower K-theory of finite groups. Comm. Alg. 8 (1980), 1927–1937.Google Scholar
Davis, J. and Lück, W.. Spaces over a category and assembly maps in isomorphism conjectures in K- and L-theory. K-Theory 15 (1998), 201–252.Google Scholar
Farrell, T. and Jones, L.. Isomorphism conjectures in algebraic K-theory. JAMS 6 (1993), 249–297.Google Scholar
Jones, L.. The converse to the fixed point theorem of P.A. Smith: I. Ann. Math. 94 (1971), 52–68.CrossRefGoogle Scholar
Milnor, J., Introduction to Algebraic $K$-theory. Annals of Mathematics Studies, Vol.72 (Princeton University Press, 1972).Google Scholar
Mislin, G., Wall's finiteness obstruction. In: Handbook of Algebraic Topology (Elsevier, 1995), pp. 1259–1291.CrossRefGoogle Scholar
Morimoto, M. and Iizuka, K.. Extendability of $G$-maps to pseudo-equivalences to finite $G$-CW-complexes whose fundamental groups are finite. Osaka J. Math. 21 (1984), 59–69.Google Scholar
Oliver, R.. Fixed-point sets of group actions on finite cyclic complexes. Comment. Math. Helvetici 50 (1975), 155–177.Google Scholar
Oliver, R. and Petrie, T.. $G$-CW-surgery and $K_0(\mathbb {Z}G)$. Math. Z. 179 (1982), 11–42.Google Scholar
Petrie, T., Pseudoequivalences of $G$-manifolds. In: Algebraic and geometric topology (Proc. Sympos. Pure Math., Stanford Univ., 1976), Part 1, 169–210, Proc. Sympos. Pure Math., 32 (Amer. Math. Soc., Providence, RI, 1978).CrossRefGoogle Scholar
Quinn, F.. Ends of maps II. Invent. Math. 68 (1982), 353–424.Google Scholar
Quinn, F.. Homotopically stratified sets. JAMS 1 (1988), 441–499.Google Scholar
Rosenberg, J., Algebraic K-Theory and its Applications. Graduate Texts in Mathematics, Vol. 147 (Springer-Verlag, 1994).Google Scholar
Smith, P. A.. Fixed-point theorems for periodic transformations. Amer. J. Math. 63 (1941), 1–8.CrossRefGoogle Scholar
Steinberger, M.. The equivariant $s$-cobordism theorem. Invent. Math. 91 (1988), 61–104.Google Scholar
Steinberger, M. and West, J.. Equivariant $h$-cobordisms and finiteness obstructions. BAMS 12 (1985), 217–220.Google Scholar
Swan, R.. Periodic resolutions for finite groups. Ann. Math. 72 (1960), 267–291.Google Scholar
Swan, R. and Evans, E. G., $K$-Theory of Finite Groups and Orders. Lecture Notes in Math., Vol.149 (Springer, 1970).CrossRefGoogle Scholar
Ullom, S.. Nontrivial lower bounds for class groups of integral group rings. Illinois J. Math. 2 (1976), 361–371.Google Scholar
Wall, C. T. C.. Finiteness conditions for CW-complexes. Ann. Math. 81 (1965), 56–69.Google Scholar
Weinberger, S., Constructions of group actions: a survey of some recent developments. Group actions on manifolds (Boulder, Colo., 1983), pp. 269–298 Contemp. Math., 36 (Amer. Math. Soc., Providence, RI, 1985).CrossRefGoogle Scholar
West, J.. Mapping Hilbert cube manifolds to ANR's: a solution of a conjecture of Borsuk. Ann. Math. 106 (1977), 1–18.Google Scholar