Article contents
Fibrewise P-universal nilpotent fibrations
Published online by Cambridge University Press: 14 November 2011
Synopsis
Let P be a set of primes. A nilpotent space X is called “P-universal”, if its P-localization canbe obtained as a direct limit over a sequence of selfmaps of X. A nilpotent fibration is called “fibrewiseP-universal”, if its fibrewise P-localization can be obtained in a similar way as a direct limit of fibrewise maps. In this paper, the following results are proved. Let π:E → B be a nilpotent fibration of connected finite or cofinite spaces. If π is fibrewise P-universal for some proper subset P of the set of primes, then its minimal model (in the sense of D. Sullivan's rational homotopy theory) admits a certaintype of weight decomposition. But the existence of such a weight decomposition implies only that there exists a finite set 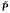 of primes, such that IT is fibrewise P-universal for all P with
of primes, such that IT is fibrewise P-universal for all P with 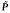 . In the absolute case however, i.e.B is a point, the set P can be chosen as the empty set. Thus a result announced by R. Body and D. Sullivan is recovered.
. In the absolute case however, i.e.B is a point, the set P can be chosen as the empty set. Thus a result announced by R. Body and D. Sullivan is recovered.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 98 , Issue 1-2 , 1984 , pp. 89 - 104
- Copyright
- Copyright © Royal Society of Edinburgh 1984
References
- 1
- Cited by


