Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T02:43:25.175Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence conditions for two-parameter eigenvalue problems†

Published online by Cambridge University Press:  14 November 2011

Paul Binding ,
Patrick J. Browne  and
Lawrence Turyn
Paul Binding
Affiliation:
Department of Mathematics and Statistics, The University of Calgary, Calgary, Alberta, Canada T2N 1N4
Patrick J. Browne
Affiliation:
Department of Mathematics and Statistics, The University of Calgary, Calgary, Alberta, Canada T2N 1N4
Lawrence Turyn
Affiliation:
Department of Mathematics and Statistics, The University of Calgary, Calgary, Alberta, Canada T2N 1N4
Get access Rights & Permissions [Opens in a new window]

Synopsis

We discuss necessary and sufficient conditions for the existence of eigentuples λ=(λl,λ2) and eigenvectors x1≠0, x2≠0 for the problem Wr(λ)xr = 0, Wr(λ)≧0, (*), where Wr(λ)= Tr + λ1Vr2, r=1,2. Here Tr and Vrs are self-adjoint operators on separable Hilbert spaces Hr. We assume the Vrs to be bounded and the Tr bounded below with compact resolvent. Most of our conditions involve the cones

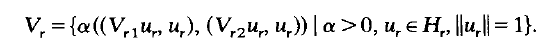
We obtain results under various conditions on the Tr, but the following is typical:

THEOREM. If (*) has a solution for all choices ofT1, T2then (a)0∉ V1UV2,(b)V1∩(—V2) =∅ and (c) V1⊂V2∪{0}, V2⊈V1∪{0}. Conversely, if (a) and (b) hold andV1⊈V2∪∩{0}, V2⊈ then (*) has a solution for all choices ofT1, T2.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 91 , Issue 1-2 , 1981 , pp. 15 - 30
Copyright
Copyright © Royal Society of Edinburgh 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Atkinson, F. V.. Multi-parameter Eigenvalue Problems, Vol. I: Matrices and Compact Operators (New York: Academic Press, 1972).Google Scholar
2Binding, P. and Browne, P. J.. A variational approach to multi-parameter eigenvalue problems in Hilbert space. SIAM J. Math. Anal. 9 (1978), 1054–1067.CrossRefGoogle Scholar
3Binding, P. and Browne, P. J.. Comparison cones for multiparameter eigenvalue problems. J. Math. Anal. Appl. 77 (1980), 132–149.Google Scholar
4Binding, P. and Browne, P. J.. Spectral properties of two-parameter eigenvalue problems.Proc. Roy. Soc. Edinburgh Sect. A 89 (1981), 157–173.CrossRefGoogle Scholar
5Bôcher, M.. The theorems of oscillation of Sturm and Klein I. Bull. Amer. Math. Soc. 4 (1898), 295–313.CrossRefGoogle Scholar
6Faierman, M.. Asymptotic formulae for the eigenvalues of a two-parameter ordinary differential equation of the second order. Canad. Math. Bull. 17 (1975), 657–665.Google Scholar
7Faierman, M.. An oscillation theorem for a two-parameter system of differential equations. Quaestiones Math. 3 (1979), 313–321.Google Scholar
8Gregus, M., Neuman, F. and Arscott, F.. Three point boundary value problems in differential equations. J. London Math. Soc. 3 (1971), 429–436.Google Scholar
9D, R. G.. Richardson. Theorems of oscillation for two linear differential equations of the second order with two-parameters. Trans. Amer. Math. Soc. 13 (1912), 22–34.Google Scholar
10Sleeman, B. D.. The two-parameter Sturm-Liouville problem for ordinary differential equations II. Proc. Amer. Math. Soc. 34 (1972), 165–170.Google Scholar
11Sleeman, B. D.. Multi-parameter Spectral Theory in Hilbert Space (London: Pitman Press, 1978).Google Scholar
12Sleeman, B. D.. Klein oscillation theorems for multiparameter eigenvalue problems in ordinary differential equations. Nieuw Arch. Wisk. 27 (1979), 341–362.Google Scholar
13Turyn, L.. Sturm-Liouville problems with several parameters. J. Differential Equations 38 (1980), 239–259.Google Scholar