Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-19T07:31:47.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and uniqueness of the global admissible solution for a viscoelastic model with relaxation

Published online by Cambridge University Press:  14 November 2011

Huijiang Zhao
Huijiang Zhao
Affiliation:
Young Scientist Laboratory of Mathematical Physics, Wuhan Institute of Mathematical Sciences, The Chinese Academy of Sciences, P.O. Box 71007, Wuhan 430071, P.R. China
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper examines the Cauchy problem for a viscoelastic model with relaxation

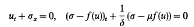
with discontinuous, large initial data, where ½ ≦ μ <1, δ > 0 are constants. We first give a definition of admissible (or entropic) solutions to the system. Under this definition, we prove the existence, uniqueness and continuous dependence of the global admissible solution for the system. Our methods are essentially due to Kruzkov, and the requirement that f(u) is not badly degenerate (more precisely, meas {x: f″(x) = 0} = 0), needed previously when considering the global existence problem for the same system, is removed.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 5 , 1996 , pp. 1113 - 1132
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ball, J. M.. Convexity conditions and existence theorems in the nonlinear elasticity. Arch. Rational Mech. Anal. 63 (1977), 337–403.CrossRefGoogle Scholar
2Chen, G. Q.. The compensated compactness method and the system of isentropic gas dynamics (MSRI 00527-91, Berkley, California, October 1990).Google Scholar
3Chen, G. Q.. Propagation and cancellation of oscillation for hyperbolic systems of conservation laws. Comm. Pure Appl. Math. 44 (1991), 121–40.CrossRefGoogle Scholar
4Chen, G. Q. and Liu, T. P.. Zero relaxation and dissipation limits for hyperbolic conservation laws. Comm. Pure Appl. Math. 46 (1993), 755–81.CrossRefGoogle Scholar
5Chuek, K. N., Conley, C. C. and Smoller, J. A.. Positively invariant regions for systems of nonlinear diffusion equations. Indiana Univ. Math. J. 26 (1977), 372–411.Google Scholar
6Dafermos, C. M.. Hyperbolic systems of conservation laws. In Systems of Nonlinear PDE, NATO Adv. Sci. Inst. Ser. C Math. Phys. Sci. 111 (1983), 27–70.Google Scholar
7Ding, X. X., Chen, G. Q. and Luo, P. Z.. Convergence of the Lax-Friedrichs scheme for isentropic gas dynamics, I, II. Acta Math. Sci. 4 (1985), 483–540.Google Scholar
8Ding, X. X. and Wang, J. H.. Global solutions for a semilinear parabolic system. Acta Math. Sci. 4 (1983), 397–412.CrossRefGoogle Scholar
9Diperna, R. J.. Uniqueness of solutions to hyperbolic conservation laws. Indiana Univ. Math. J. 28 (1979), 137–87.CrossRefGoogle Scholar
10Diperna, R. J.. Convergence of approximate solutions to conservation laws. Arch. Rational Mech. Anal. 82 (1983), 27–70.CrossRefGoogle Scholar
11Diperna, R. J.. Convergence of the viscosity method for isentropic gas dynamics. Comm. Math. Phys. 91 (1983), 1–30.CrossRefGoogle Scholar
12Glimm, J.. The continuous structure of discontinuous. Lecture Notes in Physics 344 (1989), 177–86.Google Scholar
13Greenberg, J. M. and Hsiao, L.. The Riemann problem for system u 1 + σx = 0, (σ − f(u))t + (σ − μf(u)) = 0. Arch. Rational Mech. Anal. 82 (1983), 87–108.CrossRefGoogle Scholar
14Kruzkov, S. N.. First order quasilinear equations with several space variables. Mat. USSR Sb. 10 (1970), 217–43.CrossRefGoogle Scholar
15Lax, P. D.. Hyperbolic systems of conservation laws, II. Comm. Pure Appl. Math. 10 (1957), 537–66.CrossRefGoogle Scholar
16Lax, P. D.. Shock waves and entropy. In Contributions to Nonlinear Functional Analysis, ed. Zarantonello, E. A., 603–34 (New York: Academic Press, 1971).CrossRefGoogle Scholar
17Lin, P. X.. Young measures and an application of compensated compactness to one-dimensional nonlinear elastodynamics. Trans. Amer. Math. Soc. 329 (1992), 377–413.CrossRefGoogle Scholar
18Liu, T. P.. Uniqueness of weak solutions of the Cauchy problem for general 2 × 2 conservation laws. J. Differential Equations 20 (1976), 369–98.CrossRefGoogle Scholar
19Liu, T. P.. Hyperbolic conservation laws with relaxation. Comm. Math. Phys. 108 (1987), 153–75.CrossRefGoogle Scholar
20Moraetz, C. S.. On a weak solution for a transonic flow problem. Comm. Pure Appl. Math. 38 (1985), 797–817.CrossRefGoogle Scholar
21Murat, F.. L'injection du cone positif de H−1 dans W−1,q est compacte pour tout q <2. J. Math. Pures Appl. 60 (1981), 309–22.Google Scholar
22Nishida, T. and Smoller, J. A.. Solutions in the large for some nonlinear hyperbolic conservation laws. Comm. Pure Appl. Math. 26 (1973), 183–200.CrossRefGoogle Scholar
23Smoller, J. A.. Shock waves and reaction-diffusion equations (New York: Springer, 1982).Google Scholar
24Tartar, L.. Compensated compactness and applications to PDE. In Nonlinear Analysis and Mechanics, Heriot-Watt Symposium, IV, ed. Knops, R. J., Pitman Research Notes in Mathematics 39, 136–92 (Harlow: Longman, 1979).Google Scholar
25Temple, B.. Stability and decay in systems of conservation laws. In Nonlinear Hyperbolic Problems, Proceedings, eds. Carasso, , Raviart, and Serre, (Berlin: Springer, 1986).Google Scholar
26Tveito, A. and Winther, R.. Existence, uniqueness and continuous dependence for a system of hyperbolic conservation laws modeling polymer flooding. SIAM J. Math. Anal. 22 (1991), 905–33.CrossRefGoogle Scholar
27Zhu, C. J.. Existence of the entropy solution for a viscoelastic model (Preprint, 1994).Google Scholar
28Zhu, C. J.. Global resolvability for a viscoelastic model with relaxation. Proc. Roy. Soc. Edinburgh Sect. A 125 (1995), 1277–85.Google Scholar