Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T01:47:02.063Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and uniqueness of stationary solutions of some reaction–diffusion equations arising in chemical reactor kinetics

Published online by Cambridge University Press:  14 November 2011

Jörg Swetina
Jörg Swetina
Affiliation:
Institut für theoretische Chemie und Strahlenchemie der Universität Wien, Währingerstrasse 17, A-1090 Wien, Austria
Get access Rights & Permissions [Opens in a new window]

Synopsis

In this paper we give a proof on existence of non-negative solutions of weakly coupled systems of non-linear elliptic PDE's which model isothermal chemical reactions in a bounded volume Ω. The boundaries of this “diffusion reactor” will be allowed to be differently permeable to different species, giving rise to homogeneous Neumann, or inhomogeneous mixed, boundary conditions. We assume a “conservation of mass” condition and a second condition, the choice of which is motivated in an example.

In the second section we prove that the PDE system that describes the reaction:

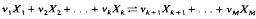
in the diffusion reactor admits a unique stationary solution.

For this proof we must show invertibility for a class of non inverse-positive linear elliptic operators.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 111 , Issue 3-4 , 1989 , pp. 249 - 263
Copyright
Copyright © Royal Society of Edinburgh 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Feinberg, M.. Complex Balancing in General Chemical Systems. Arch. Rational Mech. Anal. 49 (1972), 187–194.CrossRefGoogle Scholar
2Feinberg, M.. Mathematical aspects of mass action kinetics. In Chemical Reactor Theory: A review, eds. Lapidus, L. and Amundson, N. (Englewood Cliffs, New Jersey: Prentice-Hall, 1977).Google Scholar
3Feinberg, M.. Chemical Reaction Network Structure and the Stability of Complex Isothermal Reactors I. The Deficiency Zero and Deficiency One Theorems II. Multiple Steady States for Networks of Deficiency One. Chemical Engineering Sciences (to appear).Google Scholar
4Gilbarg, D. and Trudinger, N. S.. Elliptic Partial Differential Equations of Second Order, 2nd edn. (Berlin: Springer, 1983).Google Scholar
5Gröger, K.. On the Existence of Steady States for a Class of Diffusion–Reaction Systems. Z. Angew. Math. Mech. 65 (1985), 183–185.CrossRefGoogle Scholar
6Gröger, K.. On the Existence of Steady States of Certain Reaction–Diffusion Systems. Arch. Rational Mech. Anal. 92 (1986), 287–306.CrossRefGoogle Scholar
7Horn, F. and Jackson, R.. General Mass Action Kinetics. Arch. Rational Mech. Anal. 47 (1972), 81–116.CrossRefGoogle Scholar
8Horn, F.. Necessary and Sufficient Conditions for Complex Balancing in Chemical Systems. Arch. Rational Mech. Anal. 49 (1972), 172–186.CrossRefGoogle Scholar
9Korman, P. and Leung, A. W.. A General Monotone Scheme for Elliptic Systems with Applications to Ecological Models. Proc. Roy. Soc. Edinburgh Sect. A 102 (1986), 315–325.CrossRefGoogle Scholar
10Protter, M. H. and Weinberger, H. F.. Maximum Principles in Differential Equations (Englewood Cliffs, New Jersey: Prentice-Hall, 1967).Google Scholar
11Reed, M. and Simon, B.. Methods of Modern Mathematical Physics I: Functional Analysis (New York: Academic Press, 1972).Google Scholar
12Rumschitzki, D.. On the Theory of Multiple Steady States in Isothermal CSTRs (Thesis, University of California at Berkeley, 1984).Google Scholar
13Sattinger, D.. Monotone Methods in Nonlinear Elliptic and Parabolic Boundary Value Problems. Indiana Univ. Math. J. 21 (1972), 979–1000.CrossRefGoogle Scholar
14Siré, E. O.. Comparative Dynamics of Constrained Mass Action Kinetics. Ber. Bunsenges. Phys. Chem. 90 (1986), 1087–1091.CrossRefGoogle Scholar