In this paper we consider the nonlinear elliptic problem −Δu + αu = g(∣∇u∣) + λh(x) in Ω, u = 0 on ∂Ω, where Ω is a smooth bounded domain of ℝN, α ≥ 0, g is an arbitrary C1 increasing function and h ∈ C1(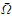) is non-negative. We completely analyse the existence and non-existence of (positive) classical solutions in terms of the parameter λ. We show that there exist solutions for every λ when α = 0 and the integral 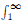1/g(s)ds = ∞, or when α > 0 and the integral 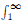s/g(s)ds = ∞. Conversely, when the respective integrals converge and h is non-trivial on ∂Ω, existence depends on the size of λ. Moreover, non-existence holds for large λ. Our proofs mainly rely on comparison arguments, and on the construction of suitable supersolutions in annuli. Our results include some cases where the function g is superquadratic and existence still holds without assuming any smallness condition on λ.