Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T01:46:04.780Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence and multiplicity of homoclinic orbits for potentials on unbounded domains

Published online by Cambridge University Press:  14 November 2011

Paolo Caldiroli
Paolo Caldiroli
Affiliation:
SISSA, via Beirut 2–4, 34014 Trieste, Italy
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the system 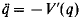in RN, where V is a potential with a strict local maximum at 0 and possibly with a singularity. First, using a minimising argument, we can prove the existence of a homoclinic orbit when the component Ω of {x ∈ RN: V(x) < V(0)} containing 0 is an arbitrary open set; in the case Ω unbounded we allow V(x) to go to 0 at infinity, although at a slow enough rate. Then we show that the presence of a singularity in Ω implies that a homoclinic solution can also be found via a minimax procedure and, comparing the critical levels of the functional associated to the system, we see that the two solutions are distinct whenever the singularity is ‘not too far’ from 0.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 124 , Issue 2 , 1994 , pp. 317 - 339
Copyright
Copyright © Royal Society of Edinburgh 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ambrosetti, A. and Bertotti, M. L.. Homoclinics for second order conservative systems. In Partial Differential Equations and Related Subjects, ed. Miranda, M., Pitman Research Notes in Math. Ser. (London: Pitman Press, 1992).Google Scholar
2Ambrosetti, A. and Coti Zelati, V.. Multiple homoclinic orbits for a class of conservative systems. Rend. Sent. Univ. Padova 89 (1993), 177–194.Google Scholar
3Bahri, A. and Rabinowitz, P. H.. A minimax method for a class of Hamiltonian systems with singular potentials. J. Funct. Anal. 82 (1989), 412–428.CrossRefGoogle Scholar
4Benci, V. and Giannoni, F.. Homoclinic orbits on compact manifolds. J. Math. Anal. Appl. 157 (1991), 568–576.CrossRefGoogle Scholar
5Coti Zelati, V., Ekeland, I. and Séré, E.. A variational approach to homoclinic orbits in Hamiltonian systems. Math. Ann. 288 (1990), 133–160.CrossRefGoogle Scholar
6Coti Zelati, V. and Rabinowitz, P. H.. Homoclinic orbits for second order Hamiltonian systems possessing superquadratic potentials. J. Amer. Math. Soc. 4 (1991), 693–727.CrossRefGoogle Scholar
7Coti Zelati, V. and Serra, E.. Multiple brake orbits for some classes of singular Hamiltonian systems (Preprint, 1991).Google Scholar
8Coti, V. Zelati and Serra, E.. Collision and non-collision solutions for a class of Keplerian-like dynamical systems (Preprint, SISSA, 1991).Google Scholar
9Gordon, W. B.. Conservative dynamical systems involving strong forces. Trans. Amer. Math. Soc. 204 (1975), 113–135.CrossRefGoogle Scholar
10Hofer, H. and Wysocki, K.. First order elliptic systems and the existence of homoclinic orbits in Hamiltonian systems. Math. Ann. 288 (1990), 483–503.CrossRefGoogle Scholar
11Lions, P. L.. The concentration-compactness principle in the calculus of variations. Rev. Mat. Iberoamericana 1 (1985), 145–201.Google Scholar
12Poincaré, H.. Les Methodes Nouvelles de la Méchanique Céleste (Paris: Gauthier–Villars, 1897–1899).Google Scholar
13Rabinowitz, P. H.. Periodic and heteroclinic orbits for a periodic Hamiltonian system. Ann. Inst. H. Poincaré Anal. Non Linéaire 6 (5) (1989), 331–346.CrossRefGoogle Scholar
14Rabinowitz, P. H.. Homoclinic orbits for a class of Hamiltonian systems. Proc. Roy. Soc. Edinburgh Sect. A 114 (1990), 33–38.CrossRefGoogle Scholar
15Rabinowitz, P. H. and Tanaka, K.. Some results on connecting orbits for a class of Hamiltonian systems. Math. Z. 206 (1991), 473–499.CrossRefGoogle Scholar
16Séré, E.. Existence of infinitely many homoclinic orbits in Hamiltonian systems. Math. Z. 209 (1992), 27–42.CrossRefGoogle Scholar
17Séré, E.. Homoclinic orbits on compact hypersurfaces in R2N, of restricted contact type (Preprint, CEREMADE, 1992).Google Scholar
18Séré, E.. Looking for the Bernoulli shift. Ann. Inst. H. Poincaré Anal. Non Lineaire 10 (5) (1993), 561–590.CrossRefGoogle Scholar
19Tanaka, K.. Homoclinic orbits for a singular second order Hamiltonian system. Ann. Inst. H. Poincaré Anal. Non Linéaire 7 (5) (1990), 427–438.CrossRefGoogle Scholar
20Tanaka, K.. Homoclinic orbits in a first order superquadratic Hamiltonian system: convergence of subharmonic orbits. J. Differential Equations 94 (1991), 315–339.CrossRefGoogle Scholar