Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T02:00:59.954Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates on the Green's function of second-order elliptic operators in ℝN

Published online by Cambridge University Press:  14 November 2011

Adrian T. Hill
Adrian T. Hill
Affiliation:
School of Mathematical Sciences, University of Bath, Claverton Down, Bath BA2 7AY, U.K., E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Sharp upper and lower pointwise bounds are obtained for the Green's function of the equation

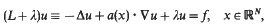
for λ> 0. Initially, in a Cartesian frame, it is assumed that 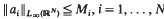. Pointwise estimates for the heat kernel of ut + Lu = 0, recently obtained under this assumption, are Laplace-transformed to yield corresponding elliptic results. In a second approach, the coordinate-free constraint 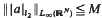is imposed. Within this class of operators, the equations defining the maximal and minimal Green's functions are found to be simple ODEs when written in polar coordinates, and these are soluble in terms of the singular Kummer confluent hypergeometric function. For both approaches, bounds on 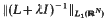are derived as a consequence.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 128 , Issue 5 , 1998 , pp. 1033 - 1051
Copyright
Copyright © Royal Society of Edinburgh 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Abramowitz, M. and Stegun, I. A.. Handbook of Mathematical Functions (Washington D.C.: National Bureau of Standards, 1964).Google Scholar
2Aronson, D. G.. Non-negative solutions of linear parabolic equations. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 22 (1968), 607–94.Google Scholar
3Dautray, R. and Lions, J.-L.. Mathematical Analysis and Numerical Methods for Science and Technology, vol. 3 (Berlin: Springer, 1990).Google Scholar
4Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.. Higher Transcendental Functions, Bateman Manuscript Project I (New York: McGraw-Hill, 1953).Google Scholar
5Erdélyi, A., Magnus, W., Oberhettinger, F. and Tricomi, F. G.. Tables of Integral Transforms, Bateman Manuscript Project I (New York: McGraw-Hill, 1954).Google Scholar
6Friedman, A.. Partial Differential Equations of Parabolic Type (Englewood Cliffs, NJ: Prentice-Hall, 1964).Google Scholar
7Henry, D.. Geometric Theory of Semilinear Parabolic Equations, Lecture Notes in Mathematics 840 (Berlin: Springer, 1981).CrossRefGoogle Scholar
8Hill, A. T.. Estimates on the heat kernel of parabolic equations with advection. SIAM J. Math. Anal. 28 (1997), 1309–16.Google Scholar
9Itô, S.. Diffusion Equations, Translations of Mathematical Monographs 114 (Providence, RI: American Mathematical Society, 1992).CrossRefGoogle Scholar
10Pazy, A.. Semigroups of Linear Operators and Applications to Partial Differential Equations, Applied Mathematical Sciences Series 44 (New York: Springer, 1983).CrossRefGoogle Scholar
11Pucci, C.. Operatori ellitici estremanti. Ann. Mat. Pura Appl. (4) 72 (1966), 141–70.Google Scholar
12Shimakura, N.. Partial Differential Operators of Elliptic Type, Translations of Mathematical Monographs 99 (Providence, RI: American Mathematical Society, 1992).Google Scholar